Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знайти нормальний вигляд квадратичної формиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Центральна гранична теорема Ляпунова Центральна гранична теорема — теорема теорії ймовірностей про збіжність розподілу суми незалежних однаково розподілених випадкових величин до нормального розподілу. Ця теорема підкреслює особливість нормального розподілу в теорії ймовірностей. Центральна гранична теорема теорії ймовірності (теорема Ляпунова) встановлює умови, за яких вказаний граничний закон є нормальним Теорема. Нехай 1. Існує таке L, що для будь-якого i має місце нерівність 2. Сума Тоді при досить великому n сума Нехай a і
З теореми Ляпунова випадкова величина
. Ця теорема дає одну з можливих відповідей на питання, чому нормально розподілені випадкові величини часто зустрічаються на практиці. Отже, суть центральної граничної теореми полягає в тому, що розподіл випадкової величини, яка формується як результат дії багатьох незалежних випадкових факторів, кожний з яких має на неї незначний вплив, мало відрізняється від нормального закону. Оскільки ці умови на практиці досить часто виконуються, то нормальний закон розподілу є найпоширенішим із законів розподілу, які зустрічаються у випадкових явищах. Розглянемо лише деякі приклади застосування центральної граничної теореми. Зокрема, в більшості випадків похибки, які виникають під час вимірювання фізичних величин, розподілені саме за нормальним законом, оскільки виникають як результат багатьох незалежних елементарних помилок, породжених різними причинами: станом приладу, атмосферними умовами, фізичним і психічним станом дослідника.
Методи навчання математики в ЗНЗ
Під методом навчання в дидактиці розуміють способи навчальної роботи вчителя і організації навчально-пізнавальної діяльності учнів з розв'язування різних дидактичних задач, спрямованих на оволодіння матеріалом, що вивчається. Крім терміна «метод навчання» в дидактиці є термін «прийом навчання», під яким найчастіше розуміють складову частину або окремий бік методу. У педагогіці існує різна класифікація методів навчання залежно від вибору основи класифікації, а саме: 1) за джерелом здобування знань (словесні, наочні, практичні), 2) за способами організації навчальної діяльності учнів (методи здобування нових знань, методи формування умінь та навичок і застосування знань на практиці, методи перевірки и оцінювання знань, умінь та навичок), 3)за характером навчально-пізнавальної діяльності учнів: а) пояснювально-ілюстративний (розповідь, лекція, пояснення, робота з підручником, демонстрації та інші.); б) репродуктивний (відтворення знань і способів дій, діяльність за алгоритмом, програмою); в) проблемний виклад; г) частково-пошуковий або евристична бесіда; д) дослідницький метод. Останні три методи використовують під час проблемного навчання як дидактичної системи. Пояснювально-ілюстративний Цим методом послуговуються, вводячи математичні поняття, вивчаючи аксіоми, теореми способи розв'язування різних класів задач. Репродуктивний Використовують при поясненні нового матеріалу, перевірки домашнього завдання (учні відтворюють розв'язання задач, формулювання і доведення теорем, означення математичних понять, правила тощо). На уроках, де формуються уміння і навички розв'язування прикладів, задач, застосування репродуктивного методу виявляється в діяльності учнів під час розв'язування вправ і задач за зразком, який дано вчителем або наведено в підручнику, в діяльності за певним алгоритмом. Проблемний виклад як метод навчання математики - полягає в тому, що, пояснюючи навчальний матеріал, учитель сам висуває проблеми і, звичайно, як правило, сам їх розв'язує. Однак постановка проблем посилює увагу учнів, активізує процес сприймання і усвідомлення того, що пояснює вчитель. Частково-пошуковий метод (його інколи називають евристичною бесідою) полягає в тому що вчитель заздалегідь готує систему питань, відповідаючи на які учні самостійно формулюють означення поняття, «відкривають» доведення теореми, знаходять спосіб розв'язування задачі. Дослідницький метод передбачає самостійний пошук розв'язання пізнавальної задачі. Причому може виявитись потреба, щоб проблему сформулював сам учень або и формулює вчитель, але розв'язують учні самостійно. Суть абстрактно-дедуктивного методу навчання полягає в тому, що під час вивчення нового матеріалу вчитель відразу сам повідомляє означення понять, що вводиться, а потім наводить конкретні приклади об’єктів, що належать до понять. Формулюється и доводиться теорема, і лише після цього розглядаються конкретні приклади застосування нового теоретичного матеріалу. Конкретно-індуктивний метод навчання протилежний абстрактно-дедуктивному методу. Під час навчання цим методом пояснення нового матеріалу починається з розгляду прикладів. Використовуючи приклади, учні мають можливість виділити суттєві ознаки поняття, що вводиться. Це допомагає самостійно чи з допомогою вчителя сформулювати означення поняття. Рисунок до теореми дасть змогу учням виявити властивості зображеної фігури і самостійно чи з допомогою вчителя сформулювати теорему. Програмоване навчання виникло з потреб вдосконалення традиційного навчання і створення кращих умов для реалізації дидактичних принципів навчання. Термін «програмоване навчання» походить від термінів програмування для ЕОМ і здійснюється за навчальними програмами.
Знайти границю функції
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.17 (0.006 с.) |



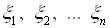 — послідовність попарно незалежних випадкових величин з математичними сподіваннями
— послідовність попарно незалежних випадкових величин з математичними сподіваннями 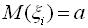 , дисперсіями
, дисперсіями 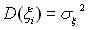 . Ці величини мають такі дві властивості:
. Ці величини мають такі дві властивості: , тобто всі значення випадкових величин, як то кажуть, рівномірно обмежені щодо їх математичних сподівань.
, тобто всі значення випадкових величин, як то кажуть, рівномірно обмежені щодо їх математичних сподівань. необмежено зростає при
необмежено зростає при  .
.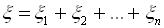 має розподіл, близький до нормального (без доведення).
має розподіл, близький до нормального (без доведення). — математичне сподівання і дисперсія випадкової величини
— математичне сподівання і дисперсія випадкової величини ;
;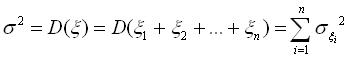 ;
; .
.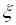 для великих значень n має розподіл, близький до нормального, тобто має місце формула
для великих значень n має розподіл, близький до нормального, тобто має місце формула (5.1)
(5.1)