Проверка нормальности распределения

Проверку нормальности распределения погрешностей обработки для ширины b, b ₁ и b ₂ можно выполнить по наибольшим показателям A и E из всех 6 независимых измерений (b_ш или b_м, b ₁₁ или b ₁₂, b ₂₁ или b ₂₂).

Для этого следует оценить значимость отношения наибольших показателей к их ошибкам:

;

Если неравенства выполняются, то асимметрия (или эксцесс) значимы и распределение не является нормальным.

Более строгим критерием для проверки нормальности считается c ² (хи-квадрат) – критерий Пирсона.

Число интервалов диапазона рассеивания рассчитывается следующим образом: r= 1 + 3,32 × lg n,
где n – число измерений в ряду. Результат округляется до целого числа.

Ручной расчет контрольного варианта выполняется в виде табл. 3.7, где m_j – частота (количество наблюдений, попавших в j –й интервал);

p_j – теоретическая вероятность попадания случайной величины в j –й интервал: p_j= F_o (t_{н j})- F_o (t_{в j});

np_j – теоретическая частота попадания значения в j –й интервал;

F_o (t_{н j}), F_o (t_{в j}) – значение нормированной функции Лапласа для нижних и верхних границ:

и

t_{н j}, t_{в j} – нормированные значения нижних и верхних границ

и .

Для расчета необходимо разбить ряд значений на интервалы. Диапазон рассеивания вычисляется по формуле

Длина интервала определяется следующим образом: . Критерий Пирсона рассчитывается по формуле . Если выполняется условие , то распределение считается нормальным с надежностью > q % (q ³ 10%).

Если не выполняется данное условие, то распределение не является нормальным с надежностью P >100- q % (q £5%).

– табличное значение критерия Пирсона: =φ(q, f),

где f=r- 3 – число степеней свободы для c ² –критерия.

В нашей работе мы находим расчетное и табличное значение c ² –критерия и делаем вывод о принадлежности нормальному распределению.

 

 

Таблица 14 – Принадлежность выборок нормальному распределению

(Федорова Л.В.)

Выборка	хи-квадрат расчетное	хи -квадрат табличное	вывод
Bisht	4,432	9,49	является нормальным
Bim	6,12	9,49	является нормальным
b1i	2,67	9,49	является нормальным
b2	7,45	9,49	является нормальным
Bp	2,77	9,49	является нормальным
bs-bр	0,97	9,49	является нормальным
Bshm	6,92	9,49	является нормальным
Tlara	1,63	9,49	является нормальным

 

Таблица 14.1 - Расчет критерия Пирсона (Федорова Л.В.)

j	границы интервалов	mj	tнj	tвj	Ф0(tнj)	Ф0(tвj)	рj	npj	(mj-npj)^2/npj
	Yнj	Yв,j
		47,583		-1,27	-0,78	-0,398	-0,282	0,116	3,132	4,776955
	47,583	48,166		-0,78	-0,299	-0,282	-0,114	0,168	4,536	0,047464
	48,166	48,749		-0,299	0,186	-0,114	0,075	0,189	5,103	0,002079
	48,749	49,332		0,186	0,672	0,075	0,248	0,173	4,671	0,096391
	49,332	49,915		0,672	1,159	0,248	0,375	0,127	3,429	3,429
	49,915	50,5		1,159	1,646	0,375	0,449	0,074	1,998	8,016018
										16,36791

r=1+3,32*lgn=1+3,32lg27 =5,75≈6

∆’=ymax-ymin=50,5-47=3,5

S=1,1992

y¯=48,525

a=∆’/r=3,5/6=0,583

χ²=∑((mj-npj)² /npj)=16,36791 > χ²_т (q=5%;f=r-3=3)=7,82.

Распределение не является нормальным с надежностью > 95%

 

Таблица 14’ – Принадлежность выборок нормальному распределению

(Санникова М.И.)

Выборка	хи-квадрат расчетное	хи -квадрат табличное	вывод
Bsh 1	1,726	9,49	является нормальным
Bmk 2	16,94	9,49	не является нормальным
Bnk 3	2,64	9,49	является нормальным
Bvk 4	2,06	9,49	является нормальным
Bcumm	18,76	9,49	не является нормальным
Bsh 1	6,2	9,49	является нормальным
Bcp	21,4	9,49	не является нормальным
Bt	5,21	9,49	является нормальным

 

Таблица 14.1’ - Расчет критерия Пирсона (Санникова М.И.)

j	границы интервалов	mj	tнj	tвj	Ф0(tнj)	Ф0(tвj)	рj	npj	(mj-npj)^2/npj
	Yнj	Yв,j
		51,966		-1,917	-1,403	-0,472	0,419	0,891	24,057	18,4311115
	51,966	52,932		-1,403	-0,89	-0,419	-0,313	0,106	2,862	0,00665409
	52,932	53,898		-0,89	-0,377	-0,313	-0,144	0,169	4,563	1,43961626
	53,898	54,864		-0,377	0,136	-0,144	0,055	0,199	5,373	0,35085222
	54,864	55,83		0,136	0,649	0,055	0,242	0,187	5,049	0,21794435
	55,83	56,8		0,649	1,165	0,242	0,377	0,135	3,645	14,841159
										35,2873375

 

r=1+3,32*lgn=1+3,32lg27 =5,75≈6

∆’=ymax-ymin=56,8-51=5,8

S=1,8814

y¯=54,6074

a=∆’/r=5,8/6=0,966

χ²=∑((mj-npj)² /npj)= 35,287>> χ²_т (q=5%;f=r-3=3)=7,82.

Распределение не является нормальным с надежностью > 95%

 

Корреляционный анализ

Предназначается для оценки степени взаимной связи двух (или более) величин.

Оценка выполняется на основании сравнения расчетного значения t_р с табличным t_Т по формуле: ,

где t_Р, t_Т – расчетное и табличное значения критерия;

– модуль коэффициента корреляции;

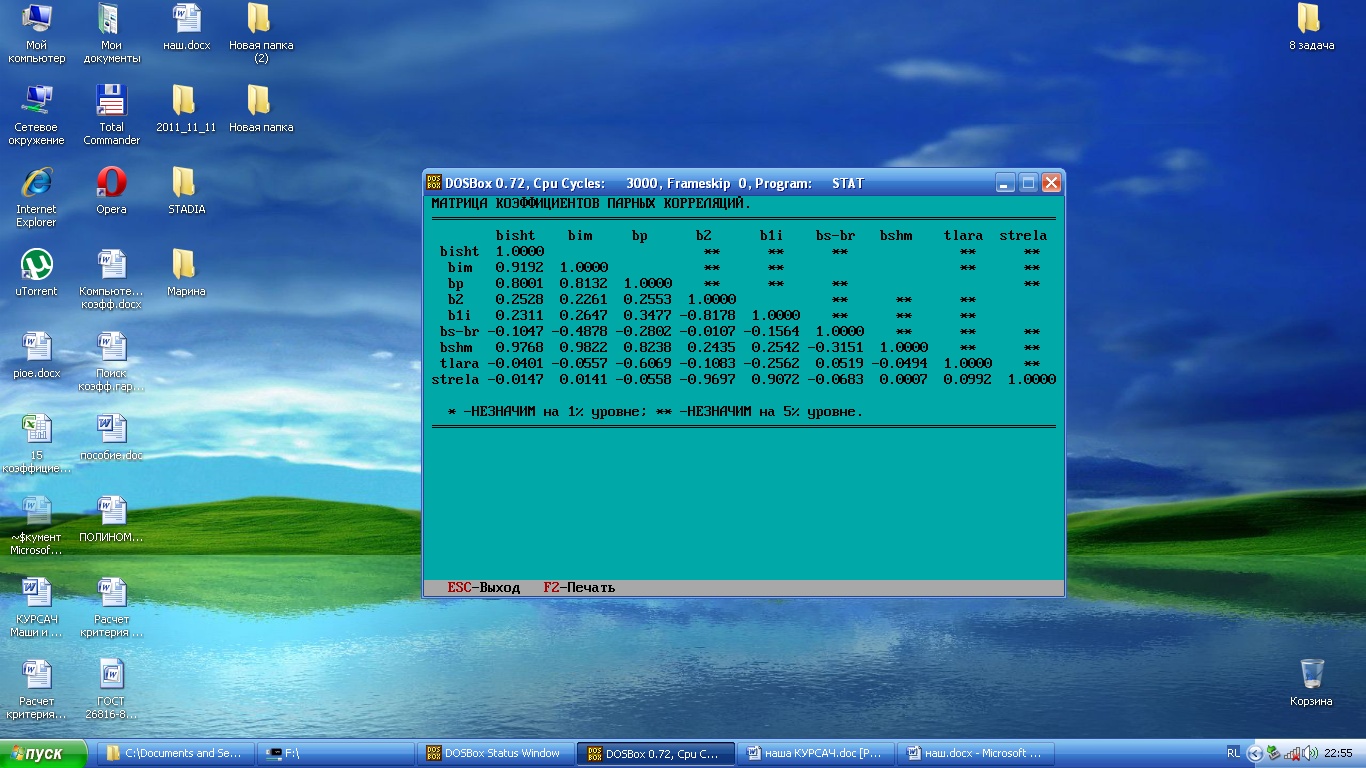
D r – ошибка коэффициента корреляции:

q – уровень значимости

f – число степеней свободы для выбора ; f = n – 2.

n – число пар значений для связанных величин.

Величина коэффициента линейной корреляции рассчитывается по формуле: , где D x_i и D y_i – отклонения значений изучаемых величин от их средних арифметических значений.

Линейная связь изучаемых величин считается значимой с надежностью P > 95%, если условие выполняется для q £ 5%; связь считается незначимой с надежностью более q %, если условие не выполняется для q ³ 10%.

Технический смысл значимой связи – подтверждение взаимной физической связи изучаемых величин. При r = 1 и D r = 0 имеем строгую прямую функциональную связь, когда каждому значению независимой переменной соответствует единственное, определенное, значение зависимой величины (функции).

При r =0 имеем две случайные, не связанные между собою, величины. При r = -1 и D r = 0 имеем строгую линейную обратную связь, когда увеличению независимой переменной соответствует уменьшение функции.

Что касается независимых измерений одной и той же величины (b_ш или b_м, b ₁₁ или b ₁₂, b ₂₁ или b ₂₂), наличие значимого t_Р говорит о статистической надежности, а r ®1 – о строгом соответствии результатов этих измерений истинному изменению измеряемых величин. И наоборот, незначимая оценка t_Р говорит о наличии больших случайных погрешностей измерений, сопоставимых с величиной истинного изменения измеряемых величин.

Значения коэффициентов корреляции для каждой пары выборок программа СТАТИСТИКА выдает в виде матрицы, в которой по главной диагонали расположены единицы (они означают корреляцию каждого ряда с самим собой и в расчет не принимаются), ниже диагонали расположены значения коэффициентов корреляции, выше – звездочки * или **, если коэффициенты незначимы на 1%-м и 5%-м уровнях соответственно, а если коэффициенты корреляции значимы, то звездочки отсутствуют.

Таблица 15 - Матрица коэффициентов парных корреляций (Федорова Л.В.)

 

 

 

 

Таблица 15’ - Матрица коэффициентов парных корреляций (Санникова М