Проверка однородности средних арифметических

Проверка однородности СА выполняется по формуле

, где и - средние значения независимых измерений каждого показателя.

При выборе табличного значения критерия Стьюдента в этой проверке число степеней свободы f_o берется суммарное: f_o=n ₁ +n ₂ -2, где n ₁, n ₂ – число измерений в каждой независимой выборке.

Оценка однородности аналогична изложенной выше для F -критерия. Технический смысл однородности средних состоит в подтверждении отсутствия систематической ошибки в результатах измерений проверяемого показателя. И наоборот, неоднородность СА независимых измерений означает наличие систематической ошибки в этих независимых измерениях.

Например, при измерении ширины доски с помощью штангенциркуля и микрометра возможна систематическая ошибка вследствие разного характера контакта этих инструментов с шероховатой поверхностью доски, а также вследствие различной величины контактных усилий при измерениях. Источником систематической ошибки при независимых измерениях разными операторами одним и тем же инструментом может служить указанное различие в величине контактных усилий, а также личные особенности базирования инструмента на доске каждым из операторов.

Решение на ЭВМ выдается в виде матрицы, в которой по главной диагонали стоит прочерк (так как выборка сама с собой не сравнивается), ниже диагонали приводятся расчетные значения критерия Стьюдента для сравниваемых выборок. Рядом с ними стоит звездочка *, если выборки неоднородны на 5%-м уровне значимости, выше указываются табличные значения критерия Стьюдента. Если выборки однородны, звездочки отсутствуют.

Таблица 12 - Проверка средних арифметических (Федорова Л.В.)

 

Таблица 12’ - Проверка средних арифметических (Санникова М.И.)

 

Проверка однородности распределения

Оценку однородности распределения независимых измерений можно выполнить по однородности показателей асимметрии и эксцесса:

;

,

где ;

,

где A₁ и A₂ – показатели асимметрии для двух сравниваемых выборок (b_ш и b_м, b ₁₁ и b ₁₂, b ₂₁ и b ₂₂);

E₁ и E₂ – показатели эксцесса для этих деталей;

S_A1, S_A2, S_E1, S_E2 – ошибки показателей асимметрии и эксцесса;

t_A, t_E, t_ТA, t_ТE – расчетные и табличные значения критерия Стьюдента для показателей асимметрии и эксцесса.

Критические значения t_ТA ³ 1,6, t_ТE ³ 2,0 для q =5%.

Оценки однородности аналогичны приведенной выше для F -критерия.

Значения СА, СКО, показателей асимметрии и эксцесса, выдаются ЭВМ по программе СТАТИСТИКА как для всех выборок, так и для каждой отдельно, значения ошибок показателей асимметрии и эксцесса – отдельно для каждой выборки.

 

Федорова Л.В.

Таблица 13 - Определение отклонений для расчета асимметрии и эксцесса по выборке b1(нижняя кромка)

	x i	D xi	D xi ^2	D xi ^3	D xi ^4
	49,1	-0,60740741	0,36894376	-0,22409917	0,1361195
		-1,50740741	2,27227709	-3,42524732	5,16324318
	48,6	-0,10740741	0,01153635	-0,00123909	0,00013309
	50,5	-2,00740741	4,0296845	-8,08921851	16,2383572
		0,492592593	0,24264746	0,119526343	0,05887779
	48,3	0,192592593	0,03709191	0,007143626	0,00137581
		1,492592593	2,22783265	3,325246507	4,96323831
	48,6	-0,10740741	0,01153635	-0,00123909	0,013309
	48,3	0,192592593	0,03709191	0,007143626	0,0013781
	48,3	0,192592593	0,03709191	0,007143626	0,00137581
	48,1	0,392592593	0,15412894	0,060509882	0,02375573
	47,9	0,592592593	0,35116598	0,208098359	0,12331755
	48,1	0,392592593	0,15412894	0,060509882	0,02375573
	47,3	1,192592593	1,42227709	1,696197124	2,02287213
	47,6	0,892592593	0,79672154	0,711147742	0,63476521
	47,3	1,192592593	1,42227709	1,696197124	2,02287213
		1,492592593	2,22783265	3,325246507	4,96323831
		1,492592593	2,22783265	3,325246507	4,96323831
	47,1	1,392592593	1,93931413	2,700674491	3,76093929
	47,3	1,192592593	1,42227709	1,696197124	2,02287213
	48,9	-0,40740741	0,1659808	-0,06762181	0,02754962
	49,2	-0,70740741	0,50042524	-0,35400452	0,25042542
	49,2	-0,70740741	0,50042524	-0,35400452	0,25042542
		-1,50740741	2,27227709	-3,42524732	5,16324318
		-1,50740741	2,27227709	-3,42524732	5,16324318
	50,5	-2,00740741	4,0296845	-8,08921851	16,2383572
	50,1	-1,60740741	2,58375857	-4,15315267	6,67580837
∑	1309,3	3,55271E-14	33,7185185	-12,6633114	80,8949084

 

;

Таблица 13.1 – Определение отклонений для расчета асимметрии и эксцесса по выборке b2(верхняя кромка)

	x i	D xi	D xi ^2	D xi ^3	D xi ^4
		0,762962963	0,582112	0,44413	0,338855
	51,3	1,462962963	2,140261	3,131122	4,580716
	53,1	-0,33703704	0,113594	-0,03829	0,012904
		1,762962963	3,108038	5,479357	9,659903
	53,8	-1,03703704	1,075446	-1,11528	1,156584
	53,2	-0,43703704	0,191001	-0,08347	0,036482
	54,6	-1,83703704	3,374705	-6,19946	11,38863
	52,3	0,462962963	0,214335	0,099229	0,045939
	53,4	-0,63703704	0,405816	-0,25852	0,164687
	53,5	-0,73703704	0,543224	-0,40038	0,295092
	53,4	-0,63703704	0,405816	-0,25852	0,164687
		-0,23703704	0,056187	-0,01332	0,003157
	52,5	0,262962963	0,06915	0,018184	0,004782
	53,1	-0,33703704	0,113594	-0,03829	0,012904
	52,7	0,062962963	0,003964	0,00025	1,57E-05
	53,2	-0,43703704	0,191001	-0,08347	0,036482
	53,2	-0,43703704	0,191001	-0,08347	0,036482
	54,3	-1,53703704	2,362483	-3,63122	5,581325
	53,2	-0,43703704	0,191001	-0,08347	0,036482
		-1,23703704	1,530261	-1,89299	2,341698
		-1,23703704	1,530261	-1,89299	2,341698
	54,1	-1,33703704	1,787668	-2,39018	3,195757
	52,1	0,662962963	0,43952	0,291385	0,193178
	51,2	1,562962963	2,442853	3,818089	5,967532
	51,4	1,362962963	1,857668	2,531933	3,450931
	50,5	2,262962963	5,121001	11,58864	26,22466
	50,5	2,262962963	5,121001	11,58864	26,22466
∑	1424,6	7,81597E-14	35,16296	20,52763	103,4962

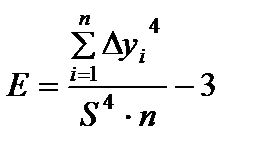
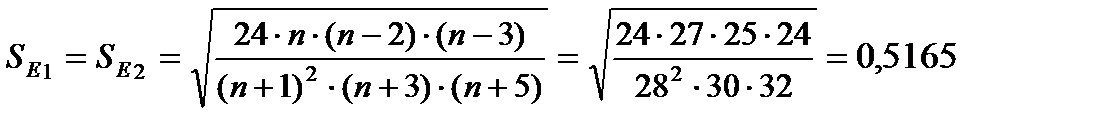
=4,312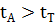

=1,65, следовательно условие не выполняется и выборки неоднородны.

=1,095

=2, следовательно условие выполняется и выборки однородны.

 

Санникова М.И.

Таблица 13’ - Определение отклонений для расчета асимметрии и эксцесса по выборке b1(нижняя кромка)

	x i	D xi	D xi ^2	D xi ^3	D xi ^4
		-3,01481	9,089108	-27,402	82,61189
	48,9	-1,91481	3,666516	-7,0207	13,44334
	48,7	-1,71481	2,94059	-5,04257	8,647069
		-1,01481	1,029849	-1,04511	1,060589
	47,7	-0,71481	0,51096	-0,36524	0,26108
	47,4	-0,41481	0,172071	-0,07138	0,029609
	47,5	-0,51481	0,265034	-0,13644	0,070243
	46,55	0,435185	0,189386	0,082418	0,035867
	46,5	0,485185	0,235405	0,114215	0,055415
	45,3	1,685185	2,839849	4,785672	8,064743
	45,5	1,485185	2,205775	3,275984	4,865444
	45,8	1,185185	1,404664	1,664787	1,973081
	45,4	1,585185	2,512812	3,983272	6,314225
	45,25	1,735185	3,010868	5,224413	9,065324
	44,4	2,585185	6,683182	17,27726	44,66493
	44,4	2,585185	6,683182	17,27726	44,66493
		1,985185	3,94096	7,823536	15,53117
	45,05	1,935185	3,744942	7,247156	14,02459
	45,45	1,535185	2,356794	3,618115	5,554476
	45,9	1,085185	1,177627	1,277943	1,386805
	46,8	0,185185	0,034294	0,006351	0,001176
	47,1	-0,11481	0,013182	-0,00151	0,000174
	47,4	-0,41481	0,172071	-0,07138	0,029609
	48,5	-1,51481	2,294664	-3,47599	5,265483
	49,2	-2,21481	4,905405	-10,8646	24,06299
	50,4	-3,41481	11,66096	-39,82	135,978
	50,5	-3,51481	12,35392	-43,4218	152,6194
∑	1268,6	-1,13687E-13	86,09407	-65,0802	580,2817

 

;

 

Таблица № 13’’ - Определение отклонений для расчета асимметрии и эксцесса по выборке b2(верхняя кромка)

	x i	D xi	D xi ^2	D xi ^3	D xi ^4
		3,607407407	13,0133882	46,944593	169,348273
		2,607407407	6,79857339	17,7266506	46,2206001
	52,5	2,107407407	4,44116598	9,35934609	19,7239553
		1,607407407	2,58375857	4,15315267	6,67580837
	54,1	0,507407407	0,25746228	0,13063827	0,06628682
	54,25	0,357407407	0,12774005	0,04565524	0,01631752
	54,3	0,307407407	0,09449931	0,02904979	0,00893012
	55,2	-0,59259259	0,35116598	-0,20809836	0,12331755
	55,2	-0,59259259	0,35116598	-0,20809836	0,12331755
	56,2	-1,59259259	2,53635117	-4,03937408	6,43307724
	56,1	-1,49259259	2,22783265	-3,32524651	4,96323831
	56,2	-1,59259259	2,53635117	-4,03937408	6,43307724
	56,3	-1,69259259	2,86486968	-4,84905721	8,20747831
	56,1	-1,49259259	2,22783265	-3,32524651	4,96323831
	56,2	-1,59259259	2,53635117	-4,03937408	6,43307724
	56,2	-1,59259259	2,53635117	-4,03937408	6,43307724
	56,5	-1,89259259	3,58190672	-6,77909013	12,8300558
	56,8	-2,19259259	4,80746228	-10,5408062	23,1116935
	56,7	-2,09259259	4,37894376	-9,16334527	19,1751484
	56,1	-1,49259259	2,22783265	-3,32524651	4,96323831
	55,65	-1,04259259	1,08699931	-1,13329743	1,18156751
	55,1	-0,49259259	0,24264746	-0,11952634	0,05887779
	54,6	0,007407407	0,00005491	0,00000041	0,000000003
	53,2	1,407407407	1,98079561	2,78778641	3,92355125
	52,7	1,907407407	3,63820302	6,93953539	13,2365212
	51,1	3,507407407	12,3019067	43,1477988	151,336909
	51,1	3,507407407	12,3019067	43,1477988	151,336909
∑	1474,4	1,592592585	92,0335185	115,27745	667,327541

 

;

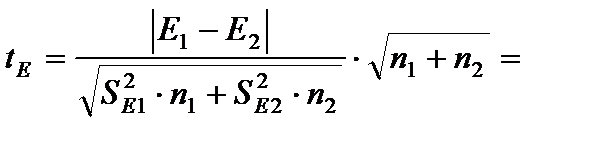
-выборки неоднородны.

-выборки неоднородны.