
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление основных статистик и аномальных погрешностей обработкиСодержание книги
Поиск на нашем сайте Основными статистическими характеристиками являются СА и СКО. СКО в математической статистике применяется в двух вариантах: выборочное СКО (S)и несмещенная оценка СКО (σ) - для генеральной совокупности. S используется при оценке различных статистических гипотез по таблицам статистических критериев, а σ требуется для прогнозирования возможной величины доверительных ошибок на основе ограниченной выборки. При числе измерений больше 10 разницей в величине S и σ можно пренебречь, так как она становится меньше 5%. На основе этих главных статистик можно оценить наличие аномальных результатов обработки (поскольку грубые ошибки измерения должны быть отсеяны на предыдущем этапе). В программе СТАТИСТИКА предусмотрены два уровня выделения аномальных отклонений: на уровне 2σ и 3σ, которые базируются на распределении Стьюдента, а так же две операции с ними: 1. исключение аномальных элементов из выборки 2. пометка аномальных отклонений условным знаком (*) в выборке. В курсовой работе мы помечаем аномальные отклонения на обоих уровнях: на уровне 3σ знаком ** на уровне 2σ знаком *
Таблица 9 - Исходные данные и проверка наличия аномальных элементов (Федорова Л.В.)
Таблица 9’- Исходные данные и проверка наличия аномальных элементов (Санникова М. И.)
Таблица 10 – Основные статистики всех выборок(Федорова Л.В.)
bisht - измерения штангенциркулем ширины доски bim - измерения микрометром ширины доски b1i- измерения штангенглубиномером нижней кромки b2 - измерения штангенглубиномером верхней кромки bp - расчетное значение ширины доски bs-bр - разность между измерениями штангенциркулем и микрометром bshm - среднее значение между измерениями штангенциркулем tlara - разность между средним значение ширины и расчетным strela - стрела прогиба
Таблица 10’ – Основные статистики всех выборок(Санникова М.И.)
Bsh 1- измерения штангенциркулем ширины доски Bmk 2 - измерения микрометром ширины доски Bnk 3- измерения штангенглубиномером нижней кромки Bvk 4 - измерения штангенглубиномером верхней кромки Bcumm - расчетное значение ширины доски Bsh 1-B - разность между измерениями штангенциркулем и микрометром Bcp - среднее значение между измерениями штангенциркулем B -разность между средним значение ширины и расчетным Bc j -стрела прогиба
Проверка однородности результатов независимых измерений Проверка однородности независимых измерений выполняется по трем показателям: 1) однородность дисперсий по F- критерию Фишера; 2) однородность средних размеров измерений по t-критерию Стьюдента; 3) однородность показателей асимметрии и эксцесса по t-критерию Стьюдента. Проверка однородности дисперсий Проверка однородности дисперсий по F -критерию Фишера выполняется по формуле
Fр, FТ – расчетное и табличное значения F -критерия FТ=φ(q, f1, f2), f1 – число степеней свободы для максимальной дисперсии; f2 – число степеней свободы для минимальной дисперсии. Если условие Fр,<FТ выполняется, то дисперсии однородны с надежностью > q%, иначе – неоднородны с надежностью P ³ ( 100- q)%. Решение на ЭВМ по программе СТАТИСТИКА выдается в виде матрицы, в которой по главной диагонали стоит прочерк (так как выборка сама с собой не сравнивается), ниже диагонали приводятся расчетные значения критерия Фишера для сравниваемых выборок. Рядом с ними стоит звездочка *, если дисперсии неоднородны на 5%-м уровне значимости, выше указываются табличные значения критерия Фишера. Если дисперсии однородны, звездочки отсутствуют. Таблица 11 - Проверка на равенство дисперсий (Федорова Л.В.)
Таблица 11’ - Проверка на равенство дисперсий (Санникова М.И.)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.91.170 (0.007 с.) |



 ,
, 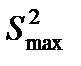 ,
,  – максимальная и минимальная дисперсии;
– максимальная и минимальная дисперсии;




