
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение личной ошибки экспериментатора минимального числа измерений в каждой точке и числа точек на доскеСодержание книги
Поиск на нашем сайте
Для определения личной ошибки необходимо выполнить многократные измерения (n=10) в одной и той же точке доски, подлежащей измерению, соответствующим инструментом. По результатам этих измерений найти СКО и определить минимальное число дублированных измерений nmin в каждой точке, необходимое для получения среднего результата с заданной надежностью (P ≥ 95%) и допускаемой погрешностью ([∆y] ≤ 0,1 для штангенциркуля (или штангенглубиномера) и ([∆y] ≤ 0,03 для измерений микрометром или индикаторным прибором):
nmin= Такие СКО и nmin надо определить при измерении ширины доски b и расстояний b1 и b2 от кромок доски до струны. Если окажется nmin ≤ 1 (или даже несколько больше 1), то измерения можно делать по 1 разу в каждой точке доски. Таблица 3 - Определение личной ошибки ширины доски для штангенциркуля (Федорова Л.В.)
Принимаем nm in=2 Так как nm in > 1, то измерения нужно проводить в каждой точке доски несколько раз.
Таблица 3’ - Определение личной ошибки ширины доски для штангенциркуля (Санникова М.И.)
Принимаем nm in=2 Так как nm in > 1, то измерения нужно проводить в каждой точке доски несколько раз.
Таблица 4 - Определение личной ошибки ширины доски для микрометра (Федорова Л.В.)
Принимаем nm in=1 Так как nm in=1, то измерения можно делать по 1 разу в каждой точке доски.
Таблица 4’ - Определение личной ошибки ширины доски для микрометра (Санникова М.И.)
Принимаем nm in=1 Так как nm in=1, то измерения можно делать по 1 разу в каждой точке доски.
Таблица 5 - Определение личной ошибки ширины доски для глубиномера (Федорова Л.В.)
Принимаем nm in=4. Так как nm in > 1, то измерения нужно проводить в каждой точке доски несколько раз.
Таблица 5’ - Определение личной ошибки ширины доски для глубиномера (Санникова М.И.)
Принимаем nm in=3. Так как nm in > 1, то измерения нужно проводить в каждой точке доски несколько раз. По результатам измерения
где
Таблица 6 - Определение толщины струны. (Федорова Л.В.)
Таблица 6’- Определение толщины струны. (Санникова М.И.)
Такое косвенное измерение t позволит оценить среднюю дисперсию воспроизводимости измерений по величине дисперсии толщины струны St2 : St2 = å(ti-t) 2 /n=Su 2 Федорова Л.В.: St2 = 4,3264/27=0,1602 Санникова М.И.: St2 =18,8613/27=0,6986 где С целью дополнительного уточнения отклонений кромок от прямолинейности следует использовать результаты независимых параллельных измерений b, b 1 и b 2 двумя разными инструментами (дополняя измерения штангенинструментами микрометрическими или индикаторными приборами) или выполняя измерения одинаковыми инструментами, но разными операторами.
Рис. 3. Посылочные риски рамной распиловки: D – длина посылки; Rm – глубина неровности Это обстоятельство необходимо учитывать при разметке контрольных точек (т.е. при определении размеров), так как величина посылки в процессе пиления бревна не остается постоянной: она может меняться от максимальной величины, заданной по режиму пиления, до нуля (в моменты пробуксовки подающих вальцов на сучках или иных выступах на бревне).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |


 2 t-коэффициент Стьюдента.
2 t-коэффициент Стьюдента.






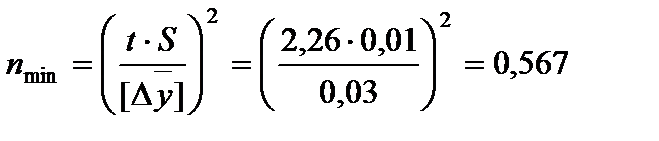
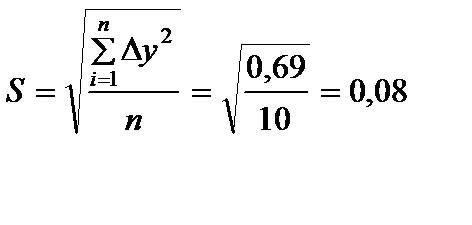

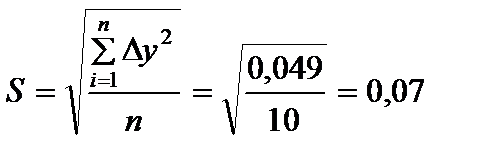

 в разных точках доски (для i=1,n) можно определить толщину струны t вместе с зазорами (или смещениями струны) при базировании штанги глубиномера по струне на «на просвет»:
в разных точках доски (для i=1,n) можно определить толщину струны t вместе с зазорами (или смещениями струны) при базировании штанги глубиномера по струне на «на просвет»:
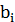 – среднее значение измерения ширины доски штангенциркулем и микрометром;
– среднее значение измерения ширины доски штангенциркулем и микрометром; - измерение расстояния от кромки до струны глубиномером
- измерение расстояния от кромки до струны глубиномером - средняя дисперсия воспроизводимости измерений, усредненная по всем точкам на длине доски и по всем трем видам прямых измерений b, b 1 и b 2 (для последующего статистического анализа адекватности уравнения регрессии).
- средняя дисперсия воспроизводимости измерений, усредненная по всем точкам на длине доски и по всем трем видам прямых измерений b, b 1 и b 2 (для последующего статистического анализа адекватности уравнения регрессии).


