
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Навчальне обладнання з математики i методика його використання.Содержание книги
Поиск на нашем сайте
Реалізація принципу наочності під час вивчення математики - необхідна умова, що забезпечує ефективність навчання й умови для запобігання формалізму. Наочність сприяє утворенню ясних і точних образів сприймання і уявлення, полегшує учням перехід від сприймання конкретних предметів до сприймання абстрактних понять про них за допомогою виявлення і словесного закріплення спільних істотних властивостей понять. Позитивний вплив наочності визначається низкою умов, зокрема правильним поєднанням слова вчителя і наочності, врахуванням вікових та індивідуальних особливостей учнів, спеціальним навчанням учнів умінню бачити наочний матеріал. Потрібно зосередити увагу учнів на тому, що саме в певному наочному матеріалі слід виокремити, порівняти, подумки перетворити. Водночас із позитивним впливом наочність може відіграти і негативну роль. Наприклад, надуживання моделями стереометричних фігур на перших уроках стереометрії може загальмувати розвиток просторових уявлень і уяви, постійне використання готового рисунка, який, наприклад, проектується на екран в процесі розв'язування геометричних задач, призводить до того, що в учнів слабко формується уміння виконувати зображення просторових фігур на площині. За одноманітного використання рисунків планіметричних фігур, наприклад прямокутних трикутників, прямих кутів у стандартному положенні (прямий кут розміщений унизу, а зовнішній кут трикутника зображується лише для гострокутних трикутників), гальмується виявлення і узагальнення істотних властивостей фігур. Увага учнів при цьому фіксується на випадкових, неістотних властивостях, відбувається їх генералізація (піднесення до ролі істотних). При цьому учні не розрізняють прямий кут, прямокутний трикутник, якщо він зображений у нестандартному, незвичайному для учнів положенні. Для уникнення цих негативних явищ важливо правильно поєднувати слова вчителя з демонстрацією наочного матеріалу. Вчитель має спрямовувати процес спостереження учня, варіювати положення фігур у наочному матеріалі, виокремлювати в ньому як істотні властивості, так і неістотні. Особливо велике значення має наочність у курсі математики 1 - 6 класів. Створення у школярів цих класів правильних геометричних образів на основі конкретних геометричних фігур і предметів довкілля є першочерговим завданням вивчення геометричного матеріалу в цих класах. Надзвичайно важливою є роль графічних зображень під час вивчення функцій в основній школі та в курсі алгебри і початків аналізу, уміння зображувати просторові фігури на площині під час вивчення стереометрії. Докладніше про це йдеться у відповідних розділах методики вивчення окремих предметів. Значну допомогу учням у вивченні алгебри і геометрії надають спеціальні прилади, які моделюють математичні поняття, задачі, графічні зображення. До них належать: магнітна дошка з координатною сіткою, переносна магнітна дошка, комплект кривих для магнітної дошки, магнітні прилади «Вимірювання площ», «Частини цілого і дроби» тощо. З успіхом використовують у школі гумові штемпелі (штампи) із зображеннями різних плоских і просторових фігур, графіків тощо. Вони допомагають заощадити навчальний час на етапі розв'язування задач, коли учні вже навчилися виконувати потрібні зображення. У процесі формування навичок виконання дій з додатними і від'ємними числами деякі вчителі використовують виготовлену в шкільних майстернях модель координатної прямої. На відшліфовану демонстраційну лінійку (дошка 150 х 15 см) наносять координатну пряму з просвердленими отворами для фіксування точок, що відповідають додатним і від'ємним числам. Аналогічні моделі координатної прямої можна виготовити зі звичайних пластмасових або дерев'яних лінійок. Спочатку учні виконують дії на моделі і, помітивши закономірності в отриманні результатів, під керівництвом учителя колективно формулюють відповідні правила. Поширеним засобом наочності є математичні таблиці. Здебільшого їх виготовляють у школі учні й вчителі. Використання наочності на уроці повинно бути цілеспрямованим і методично виправданим. А це вимагає серйозного підходу до їх адекватного вибору. Отже, доцільно виділити такі вимоги до використання наочності у навчальному процесі початкової школи: 1) відповідність наочності змісту виучуваного матеріалу; 2) виділення найважливіших ознак предмета; 3) естетичне оформлення наочності; 4) вчасне використання наочності; 5) помірне використання наочності; 6)відповідність наочності психологічним закономірностям сприймання; 7) інтерес учнів до розглядуваних наочних об’єктів; 8) зв’язок змісту наочного посібника з досвідом учнів.
3. Знайти на кривiй y = x 3 точку M(a; b), дотична в якiй до даної кривої паралельна хордi, що з’єднує точки A(−1
4. Обчислити сигнатуру квадратичної форми f =
1. Метод Фурє Нехай необхідно знайти розв’язок диференціального рівняння
Алгоритм методу. 1. Представляємо розв’язок у вигляді 2. Знаходимо власні значення і власні функції задачі Штурма-Ліувілля 3. Для кожноговласного значення 4.Складаємо ряд 5. Невідомі коефіцієнти Розглянемо докладно алгоритм. Шукаємо нетривіальні розв’язки рівняння (1), які задовольняють крайові умови (3), у вигляді
Підставивши (5) у рівняння (1) і розділивши змінні, одержимо остання рівність можлива тоді і тільки тоді, коли
Підставивши (5) у крайові умови (3), одержимо
Таким чином, нам потрібно знайти ненульові розв’язки рівняння (6) і крайової задачі (7), (8). Задача (7), (.8) не для всяких Означення. Ті значення параметра Задача (7), (8) знаходження власних значень і власних функцій називається задачею Штурма-Ліувілля. Знайдемо власні значення та власні функції. Для цього розглянемо окремо випадки, коли а) нехай Підставивши знайдений розв’язок у крайові умови (8), одержимо
при Підставивши його в крайові умови (8), матимемо в) нехай
Задача (7), (8) буде мати нетривіальні розв’язки тільки тоді, коли
Знайденим власним значенням відповідають власні функції Підставивши знайдені власні значення у рівняння (6) і проінтегрувавши його, одержимо
де Розглянемо ряд
Нехай функції
Порівнюючи ряди (12), (13), одержуємо Підставивши знайдені коефіцієнти у (9), одержимо розв’язок задачі (1) - (.3):
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.166 (0.009 с.) |





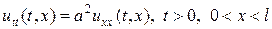 , (1) який задовольняє рівняння
, (1) який задовольняє рівняння 
 (2) і крайові умови
(2) і крайові умови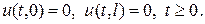 (3) В силу умов узгодженості
(3) В силу умов узгодженості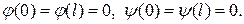 (4)
(4)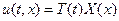 і розв’язуємо задачу Штурма-Ліувілля
і розв’язуємо задачу Штурма-Ліувілля знаходимо загальний розвязок
знаходимо загальний розвязок 
 =
= 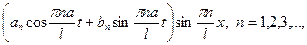
 і
і  , знаходимо, використовуючи початкові умови, отримаємо
, знаходимо, використовуючи початкові умови, отримаємо 

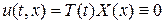 (5)
(5)
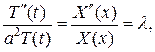
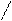
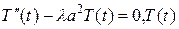 º 0, (6)
º 0, (6)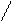

 º 0.(7)
º 0.(7)
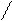 Оскільки
Оскільки 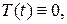 то із останніх рівностей маємо
то із останніх рівностей маємо  (8)
(8)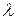 має нетривіальні розв’язки.
має нетривіальні розв’язки. Тоді загальний розв’язок рівняння (7) має вигляд
Тоді загальний розв’язок рівняння (7) має вигляд 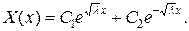
 Визначник системи
Визначник системи 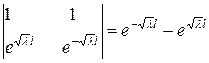
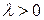 відмінний від нуля, тому система має тільки нульовий розв’язок
відмінний від нуля, тому система має тільки нульовий розв’язок  ,тобто
,тобто  . Таким чином,
. Таким чином,  загальний розв’язок рівняння (7) рівний
загальний розв’язок рівняння (7) рівний  .
. ,
,  . Отже,
. Отже,  і,
і,  . Тоді загальний розв’язок рівняння (7) має вигляд
. Тоді загальний розв’язок рівняння (7) має вигляд

 , а
, а 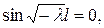 тобто коли
тобто коли ,
, 
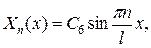 які визначаються з точністю до сталого множника. В зв’язку з цим надалі будемо вважати, що
які визначаються з точністю до сталого множника. В зв’язку з цим надалі будемо вважати, що  .
. Згідно з (5) функції
Згідно з (5) функції
 ,
,  ,задовольняють рівняння (1) і крайові умови (3.3) при довільних
,задовольняють рівняння (1) і крайові умови (3.3) при довільних 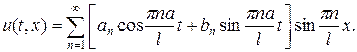 (3.9) Для побудови розв’язку мішаної задачі (1)-.3) залишилось у ряді (9) так вибрати коефіцієнти
(3.9) Для побудови розв’язку мішаної задачі (1)-.3) залишилось у ряді (9) так вибрати коефіцієнти  і
і  є кусково-диференційовними на проміжку
є кусково-диференційовними на проміжку  . Тоді їх можна розкласти в ряди Фур’є
. Тоді їх можна розкласти в ряди Фур’є (13) де
(13) де

 (14)
(14)


