Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні елементарні функції та їх графіки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вивчаючи те чи інше явище, ми часто змушені мати справу з величинами, які пов’язані між собою так, що зміна деяких з них приводить до зміни інших. Такий взаємозв’язок у математиці виражається за допомогою поняття функції. Наприклад площа круга радіуса
Дамо тепер означення функції. Означення. Якщо кожному числу Змінна Множина Розглянуті у попередніх параграфах послідовності теж можна розглядати як функції, область визначення яких є множина
Функцію можна задавати різними способами. 1. Аналітичний спосіб. Це спосіб задання функції за допомогою формули (аналітичного виразу):
Наприклад, формула Аналітичний спосіб має як свої переваги, так і свої недоліки. До переваг відносяться компактність, зручність при проведенні теоретичних досліджень та ін. До недоліків – відсутність наочності, необхідність проводити обчислення для знаходження значень функції та ін. 2. Табличний спосіб. Це спосіб задання функції за допомогою таблиці, яка містить значення функції при деяких обраних значеннях аргументу:
Тут Наприклад, для функції
Цей спосіб часто використовують при проведенні експериментів, коли задають певну сукупність Цей спосіб також має переваги та недоліки. До переваг відноситься те, що не треба обчислювати значення функції (вони вже є у таблиці) До недоліків громіздкість (таблиці займають багато місця), відсутність наочності, а також те, що принципово неможливо без додаткової інформації знайти значення функції для тих значень аргументу, які не входять до таблиці (а іноді це треба робити). Правда, якщо є деяка додаткова інформація про властивості функції, то можна наближено знайти ці значення за допомогою так званої інтерполяції. 3. Графічний спосіб. Це спосіб задання функції за допомогою графіка, тобто множини точок на координатній площині, прямокутні координати
Графічним способом широко користуються при дослідженнях, пов’язаних з використанням таких засобів, як барограф (для запису змін атмосферного тиску), осцилограф (для запису змін електричного струму, чи напруги), електрокардіографа (для запису електричних явищ, пов’язаних з діяльністю серця), термографа (для запису температури повітря) тощо. Криві (відповідно барограма, осцилограма, електрокардіограма, термограма), які виписують ці прилади, задають певну функцію, властивості якої характеризують перебіг того, чи іншого процесу.
До переваг графічного способу відноситься, перш за все, наочність (те, чого не мають аналітичний та табличний способи). Маючи графік, можна наочно уявити собі характер процесу, який цим графіком описується. Разом з цим графічний спосіб має і недоліки: громіздкість, лише наближене уявлення про значення функції при конкретних значеннях аргументу. 4. Словесний спосіб. Існують функції, які складно, або взагалі неможливо задати формулою, а також неможливо побудувати графік. Деякі з таких функцій можна описати просто за допомогою слів. Класичним прикладом такої функції є так звана функція Діріхле:
Графік цієї функції практично зобразити не можна, оскільки він складається з точок прямої Функції, з якими ми у подальшому будемо мати справу, складаються з порівняно невеликого числа функцій, які називаються основними елементарними функціями. До них відносяться наступні функції. 1. Сталі функції, або константи. Це функції виду
Рис. 17.
2. Степеневі функції. Це функції вигляду 1)
Рис. 18.
2) 3)
4)
Рис. 20.
5)
Рис. 21.
6)
Рис. 22.
3. Показникові функції:
1)
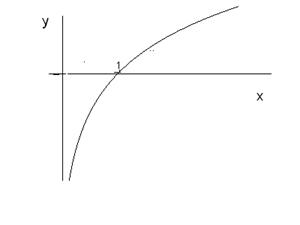
Зокрема, до таких функцій належить й славнозвісна експонента, про яку вже згадувалося, але детальніше буде йтися у подальшому. 4. Логарифмічні функції:
1)
Рис. 24 (а). Рис. 24 (б).
5. Тригонометричні функції:
1)
Рис. 25 (а).
2)
Рис. 25 (б).
3)
Рис. 26 (а).
4)
Рис. 26 (б).
6. Обернені тригонометричні функції.
1)
2)
Рис. 27 (б).
3)
Рис. 28 (а).
4)
Рис. 28 (б).
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1836; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.254.189 (0.009 с.) |

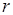 виражається формулою:
виражається формулою: 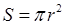 . Змінюючи радіус
. Змінюючи радіус  є функцією його радіуса
є функцією його радіуса 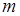 та
та 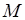 взаємодіють між собою, виражається формулою:
взаємодіють між собою, виражається формулою: , де
, де  – відстань між центрами тіл,
– відстань між центрами тіл, 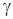 – універсальна гравітаційна стала. Залишаючи
– універсальна гравітаційна стала. Залишаючи  та
та  незмінними, ми можемо змінювати відстань
незмінними, ми можемо змінювати відстань  , тобто ми можемо сказати, що
, тобто ми можемо сказати, що  з деякої числової множини
з деякої числової множини  за певним законом поставлено у відповідність одне і тільки одне число
за певним законом поставлено у відповідність одне і тільки одне число  з числової множини
з числової множини 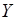 , то кажуть, що на множині
, то кажуть, що на множині  .
. ми розуміємо як раз той самий закон, за яким встановлюється відповідність, тобто ті операції, які треба виконати над аргументом
ми розуміємо як раз той самий закон, за яким встановлюється відповідність, тобто ті операції, які треба виконати над аргументом  . Множина
. Множина  . Наприклад, для функції
. Наприклад, для функції  областю визначення є відрізок
областю визначення є відрізок 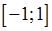 , а множиною значень відрізок
, а множиною значень відрізок  . Декільком різним значенням аргументу
. Декільком різним значенням аргументу 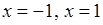 відповідає одне й те ж значення функції
відповідає одне й те ж значення функції 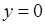 . Але наведене означення функції забороняє ситуацію, коли одному й тому ж значенню аргументу відповідає декілька різних значення функції. Хоча в інших розділах математичного аналізу, наприклад теорії функцій комплексної змінної, розглядаються і такі (так звані багатозначні) функції.
. Але наведене означення функції забороняє ситуацію, коли одному й тому ж значенню аргументу відповідає декілька різних значення функції. Хоча в інших розділах математичного аналізу, наприклад теорії функцій комплексної змінної, розглядаються і такі (так звані багатозначні) функції.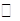 :
:
 .
. – це аналітичний спосіб задання функції, яка кожному дійсному значенню аргументу
– це аналітичний спосіб задання функції, яка кожному дійсному значенню аргументу  .
.



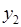
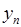
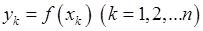 .
. ця таблиця може мати такий вигляд:
ця таблиця може мати такий вигляд: значень аргументу і дослідним шляхом знаходять відповідні значення функції
значень аргументу і дослідним шляхом знаходять відповідні значення функції  . Крім того, табличний спосіб широко застосовується при розв’язанні математичних задач за допомогою комп’ютерів, коли вихідну інформацію комп’ютер видає у вигляді числових масивів (таблиць). Зі школи вам знайомі відомі «Чотиризначні математичні таблиці» В.М.Брадіса.
. Крім того, табличний спосіб широко застосовується при розв’язанні математичних задач за допомогою комп’ютерів, коли вихідну інформацію комп’ютер видає у вигляді числових масивів (таблиць). Зі школи вам знайомі відомі «Чотиризначні математичні таблиці» В.М.Брадіса. яких задовольняють рівність
яких задовольняють рівність  Рис. 16.
Рис. 16.
 , які мають раціональні абсциси, і точок прямої
, які мають раціональні абсциси, і точок прямої  (тобто у кожній точці така функція приймає одне й те ж значення). Областю визначення
(тобто у кожній точці така функція приймає одне й те ж значення). Областю визначення  , а множиною значень
, а множиною значень  . Графіком такої функції є пряма лінія, яка паралельна осі абсцис і проходить через точку
. Графіком такої функції є пряма лінія, яка паралельна осі абсцис і проходить через точку 
 , де
, де  . Область визначення і множина значень такої функції залежить від
. Область визначення і множина значень такої функції залежить від  . Наведемо деякі приклади таких функцій та їх графіків.
. Наведемо деякі приклади таких функцій та їх графіків. ;
;  .
.
 . Графік наведено на рис. 16.
. Графік наведено на рис. 16. . Графіком є так звана кубічна парабола:
. Графіком є так звана кубічна парабола: Рис. 19.
Рис. 19. .
.
 . Графіком такої функції є гіпербола:
. Графіком такої функції є гіпербола:
 .
.
 . Характер графіка функції залежить від числа
. Характер графіка функції залежить від числа  :
: 2)
2) 
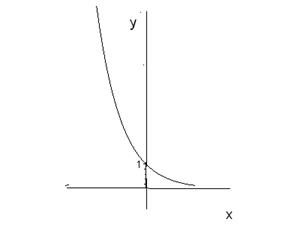
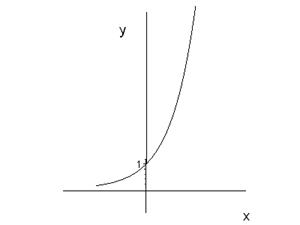 Рис. 23 (а). Рис. 23 (б).
Рис. 23 (а). Рис. 23 (б). . Характер графіка також залежить від числа
. Характер графіка також залежить від числа 
 .
.



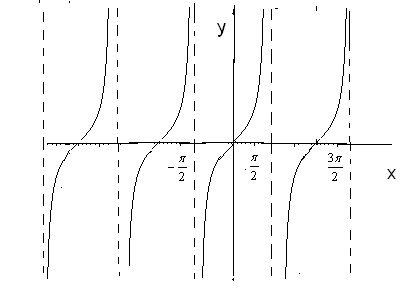



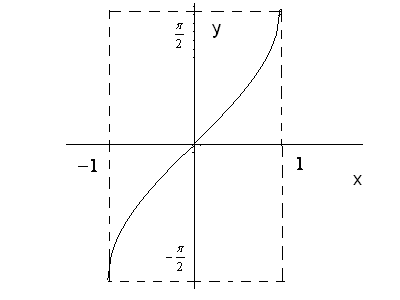 Рис. 27 (а).
Рис. 27 (а).
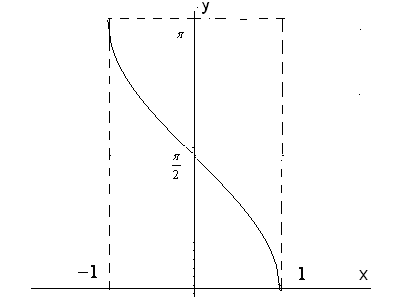
 .
.