
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементарні функції та їх класифікація.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Деякі важливі типи функцій. Означення. Елементарною функцією називається така функція, яка утворюється з основних елементарних функцій за допомогою скінченного числа операцій додавання, віднімання, множення і ділення, а також операції суперпозиції. Зауважимо, що тут термін «елементарна» не означає проста. Неелементарні функції можуть бути набагато простішими, ніж елементарні. Наприклад функція
Елементарні функції розділяються на наступні основні класи. 1. Многочлени (або поліноми). Многочленом (поліномом) степеня
Дійсні числа 2. Раціональні функції. Це функції, які є відношенням двох многочленів (не обов’язково однакового степеня):
Наприклад:
Зокрема, многочлени являються частинним випадком раціональних функцій ( 3. Ірраціональні функції Це функції, які утворюються за допомогою скінченого числа арифметичних дій та операцій суперпозиції з раціональних функцій та степеневих з раціональними показниками. Наприклад:
Раціональні та ірраціональні функції називаються алгебраїчними. Графіки цих функцій відповідно називаються алгебраїчними кривими. До них, зокрема, відносяться вже відомі вам еліпс, гіпербола і парабола (див. «Аналітична геометрія на площині»). 4. Трансцендентні функції. До цих функцій відносяться ті елементарні функції, які не являються алгебраїчними. Це, зокрема, всі тригонометричні та обернені тригонометричні функції, а також показникові та логарифмічні. Виділимо деякі важливі типи функцій (вони стосуються не лише елементарних функцій), з якими у подальшому нам доведеться мати справу. 1. Обмежені функції. Означення. Функція Іншими словами значення обмеженої функції не виходять за межі відрізку
Рис. 35.
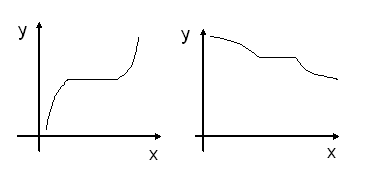
Одна й та ж функція на одній множині може бути обмеженою, а на іншій ні. Наприклад, функція 2. Монотонні функції. Означення. Функція Тобто для зростаючої функції більшому значенню аргумента відповідає і більше значення функції, а для спадної більшому значенню аргумента відповідає менше значення функції. Означення. Функція Тобто для неспадної функції більшому значенню аргумента відповідає не менше значення функції, а для незростаючої більшому значенню аогумента відповідає не більше значення функції. Схематичні графіки цих функцій зображено на рис. 36 (а – зростаюча, б – спадна, в – неспадна, г – незростаюча).
Рис. 36 (а). Рис. 36 (б).
Рис. 36 (в). Рис. 36 (г).
Одна й та ж функція на одних ділянках числової прямої може бути зростаючою, а на інших спадною. Наприклад, функція Зростаючі, спадні, неспадні та незростаючі функції називаються монотонними функціями. При цьому зростаючі та спадні функції називаються строго монотонними. Як відмічалося в п. 16, функція 3. Парні та непарні функції. Означення. Функція З означення випливає, що область визначення парної чи непарної функції обов’язково симетрична відносно точки
Рис. 37 (а). Рис. 37 (б).
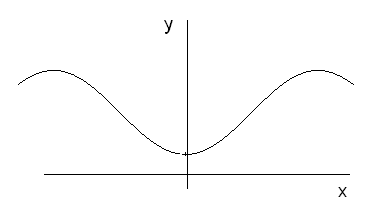
З основних елементарних функцій парними є, наприклад, Не слід вважати, що, якщо функція не є парною, то вона непарна. Існує скільки завгодно функцій, які не являються ні парними, ні непарними. Наприклад Для побудови графіка парної чи непарної функції достатньо побудувати її графік тільки у правій півплощині, а потім відобразити симетрично відносно осі 4. Періодичні функції. Означення. Функція Число З основних елементарних функцій періодичними є тільки тригонометричні функції. Основний період функцій Для побудови графіка функції, періодичної з періодом
18.Границя функції у точці та у нескінченності. Однобічні границі. Спробуємо тепер означення границі послідовності, яке було дано у п.9, узагальнити на випадок функції Означення. Число У цьому випадку ми пишемо:
Наведене означення називається означенням функції на мові послідовностей, або означенням Гейне. * Існує ще одне означення границі функції, яке полягає у наступному. В п.8 ми інтуїтивно ввели поняття границі функції, як деякого числа
Означення. Число У цьому випадку пишемо: У символьній формі запису це означення має такий вигляд:
Саме таку форму ми будемо використовувати у подальшому. Наведене означення називається означенням границі функції на мові «
Рис. 38.
Теорема. Означення границі функції за Гейне та за Коші еквівалентні. Доведення. Нехай Нехай тепер
В той же час:
Якщо у якості Теорему доведено. Приклади. 1. Доведемо, що
Нехай тепер 2. Довести, що Знову використаємо означення Коші. Задамо довільне
Якщо 3. Доведемо, що функція Тепер розглянемо іншу послідовність Отже, для двох різних послідовностей значень аргумента, прямуючих до нуля, відповідні послідовності значень функції мають різні границі – 0 і 1. І тоді, згідно з означенням Гейне, наша функція не має границі при Вище ми вже відмічали, що не слід змішувати поняття границі функції
Доведемо, що
Може бути і така ситуація, коли функція визначена у точці
Ця функція визначена у точці В наведених означеннях границі функції значення аргументу Означення. Число Тоді пишемо:
Це означення за змістом близько до означення границі послідовності, тому особливих пояснень не вимагає. Сама границя функції теж може бути нескінченною. Означення. Кажуть, що границя функції Тоді пишемо: Тобто за рахунок достатньої близькості аргументу У цьому випадку функція Приклад. Довести, що функція Задамо довільне
Якщо Границя функції може дорівнювати не просто нескінченності, а нескінченності з певним знаком. Означення. Кажуть, що Наприклад: Завдання. Самостійно сформулюйте означення того що функція Введемо поняття однобічних границь функції. Означення. Число У цьому випадку пишемо: Означення. Число У цьому випадку пишемо: Тобто у першому означенні Приклади. 1. Покажемо, що 2. Покажемо, що Нехай спочатку Той факт, що
Рис. 39.
Доведення. Нехай спочатку Нехай тепер
|
||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 1884; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

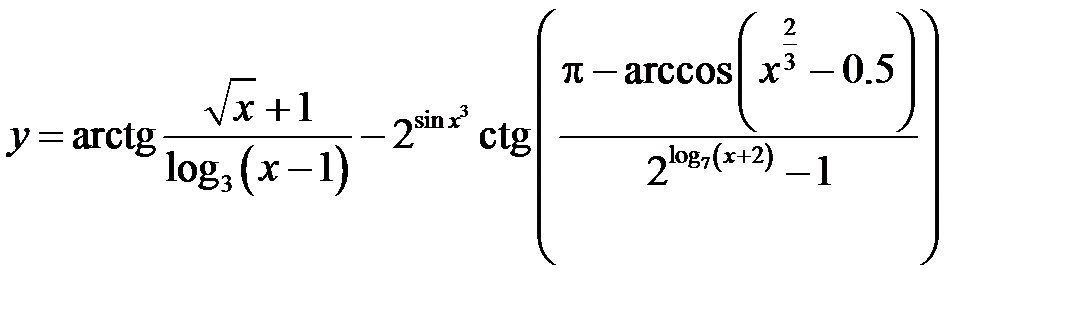 є елементарною (всі потрібні умови виконано). А функція
є елементарною (всі потрібні умови виконано). А функція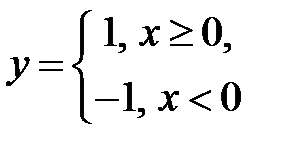 елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції
елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції 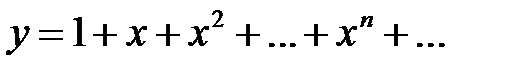 (нескінченна кількість арифметичних дій),
(нескінченна кількість арифметичних дій),  (відповідно ціла і дробова частина
(відповідно ціла і дробова частина 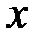 ), розглянута вище функція Діріхле та ін. До неелементарних відносяться також так звані спеціальні функції, які відіграють дуже важливу роль у природознавстві. Завдяки фізикам, в математику увійшли й функції більш складної природи – так звані узагальнені функції.
), розглянута вище функція Діріхле та ін. До неелементарних відносяться також так звані спеціальні функції, які відіграють дуже важливу роль у природознавстві. Завдяки фізикам, в математику увійшли й функції більш складної природи – так звані узагальнені функції.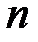 називається функція вигляду:
називається функція вигляду: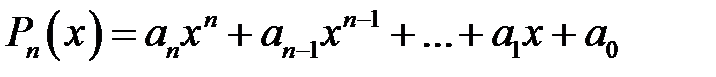 .
.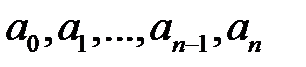 називаються коефіцієнтами многочлена. Зокрема, якщо
називаються коефіцієнтами многочлена. Зокрема, якщо  , то
, то  . Якщо
. Якщо  , то
, то 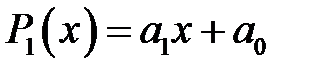 – лінійна функція. Якщо
– лінійна функція. Якщо 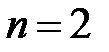 , то
, то 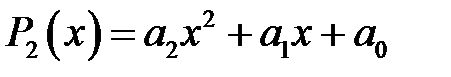 – квадратний тричлен.
– квадратний тричлен. .
.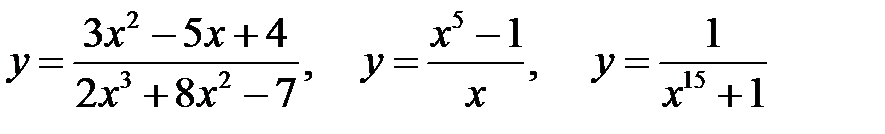 .
. ).
). .
. називається обмеженою на множині
називається обмеженою на множині  , якщо
, якщо  таке, що
таке, що  .
.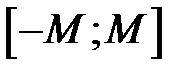 . З геометричної точки зору це означає, що її графік цілком лежить між прямими
. З геометричної точки зору це означає, що її графік цілком лежить між прямими 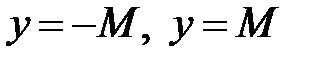 (рис. 35).
(рис. 35).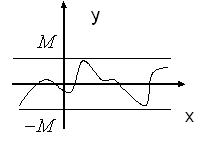
 обмежена на відрізку
обмежена на відрізку 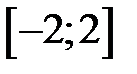 (на ньому
(на ньому 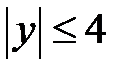 ) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція
) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція  обмежена на відрізку
обмежена на відрізку 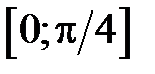 (тут
(тут  ), але не обмежена на півінтервалі
), але не обмежена на півінтервалі 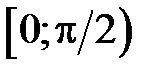 . Функція
. Функція 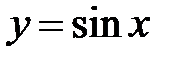 обмежена на всій числовій прямій (
обмежена на всій числовій прямій (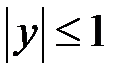 ).
).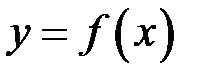 називається зростаючою (спадною) на множині
називається зростаючою (спадною) на множині 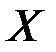 , якщо
, якщо 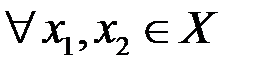 таких, що
таких, що 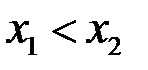 , виконана нерівність
, виконана нерівність 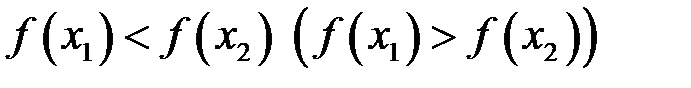 .
.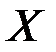 , якщо
, якщо 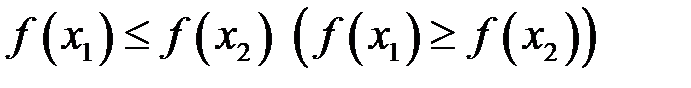 .
.
 спадна на
спадна на  і зростаюча на
і зростаюча на 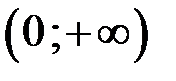 .
.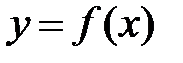
 має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами
має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами 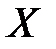 та
та  . Таку властивість мають, зокрема, строго монотонні функці. Дійсно, для зростаючої функції з нерівності
. Таку властивість мають, зокрема, строго монотонні функці. Дійсно, для зростаючої функції з нерівності 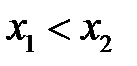 випливає нерівність
випливає нерівність  , а для спадної з нерівності
, а для спадної з нерівності 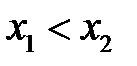 випливає нерівність
випливає нерівність 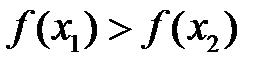 . Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція
. Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція 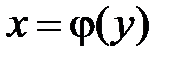 також зростає (спадає).
також зростає (спадає).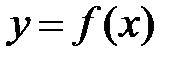 називається парною (непарною), якщо.
називається парною (непарною), якщо. 
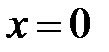 . Графік парної функції симетричний відносно осі
. Графік парної функції симетричний відносно осі  (рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)).
(рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)).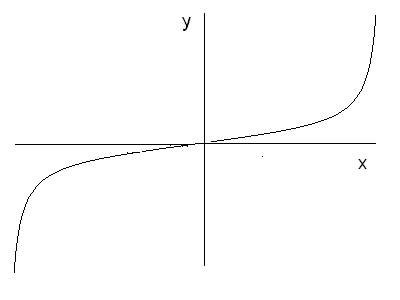
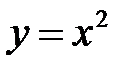 ,
, 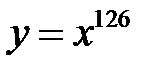 ,
, 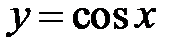 , а непарними
, а непарними 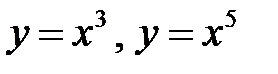 ,
, 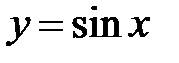 ,
,  ,
, 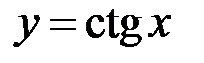 ,
,  .
.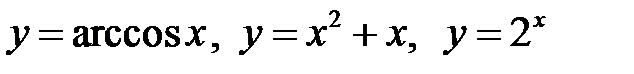 тощо.
тощо. (для парної функції), або відносно початку координат (для непарної функції).
(для парної функції), або відносно початку координат (для непарної функції). називається періодичною, якщо існує таке
називається періодичною, якщо існує таке 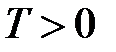 , що
, що 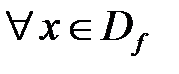 виконано:
виконано: 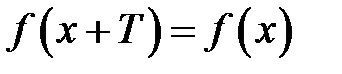 .
.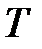 називається періодом функції. Очевидно, що періодом буде також будь яке число виду
називається періодом функції. Очевидно, що періодом буде також будь яке число виду 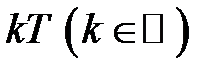 . Найменший з додатних періодів називається основним періодом функції.
. Найменший з додатних періодів називається основним періодом функції. дорівнює
дорівнює  , а функцій
, а функцій 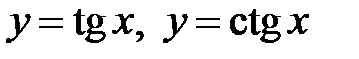 дорівнює
дорівнює  .
.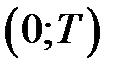 ), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини
), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини 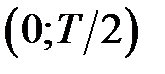 .
.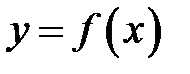 . Візьмемо деяку послідовність
. Візьмемо деяку послідовність 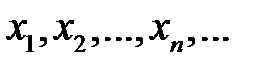 значень аргумента
значень аргумента  , яка збігається до числа
, яка збігається до числа 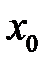 , тобто
, тобто 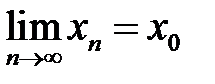 . Тоді відповідно значення функції
. Тоді відповідно значення функції  також будуть утворювати деяку послідовність
також будуть утворювати деяку послідовність 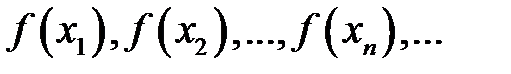
 називається границею функції
називається границею функції 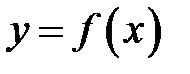 при
при 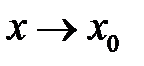 (або у точці
(або у точці  ), якщо для будь якої послідовності
), якщо для будь якої послідовності 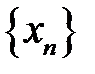 значень аргумента
значень аргумента 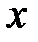 , такої, що
, такої, що 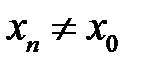 , і
, і 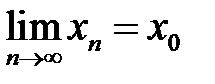 , відповідна послідовність значень функції
, відповідна послідовність значень функції 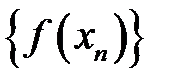 збігається до числа
збігається до числа  .
.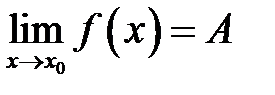 .
.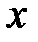 «наближаються» (прямують) до числа
«наближаються» (прямують) до числа  . Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргументу
. Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргументу  . Це буде означати, що
. Це буде означати, що , (18.1) тобто значення аргументу
, (18.1) тобто значення аргументу 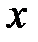 потрапляють в
потрапляють в 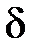 -окіл точки
-окіл точки 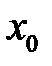 . Другу з цих мір позначимо як
. Другу з цих мір позначимо як 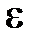 . Це буде означати, що
. Це буде означати, що , (18.2) тобто значення функції
, (18.2) тобто значення функції 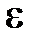 -окіл точки
-окіл точки  . За рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості
. За рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості 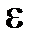 . Іншими словами за заданим числом
. Іншими словами за заданим числом  ми повинні знайти число
ми повинні знайти число 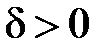 , яке залежить від
, яке залежить від 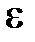 , таке, що виконання нерівності (18.1) забезпечує і виконання нерівності (18.2). Саме цей факт виражає наступне означення.
, таке, що виконання нерівності (18.1) забезпечує і виконання нерівності (18.2). Саме цей факт виражає наступне означення.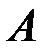 називається границею функції
називається границею функції 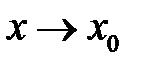 (або у точці
(або у точці 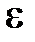 існує таке додатне число
існує таке додатне число 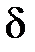 , яке залежить від
, яке залежить від 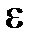 , що для будь яких значень
, що для будь яких значень 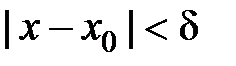 , а також
, а також 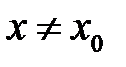 , виконано нерівність
, виконано нерівність 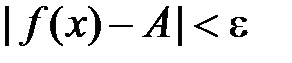 .
.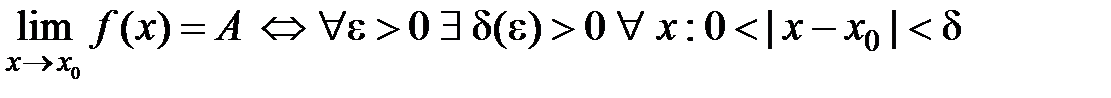
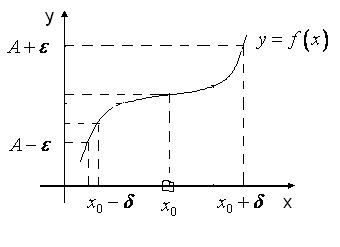
 .
.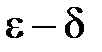 », або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу
», або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу 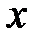 належать множині
належать множині 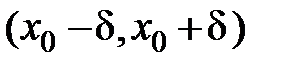 , тобто
, тобто 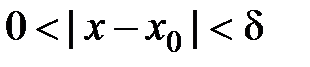 , то значення функції
, то значення функції  належать проміжку
належать проміжку  , тобто
, тобто 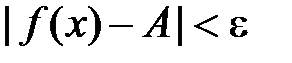 .
.
 у сенсі Коші. Тоді
у сенсі Коші. Тоді 
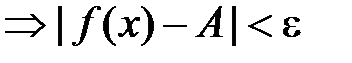 . Оберемо довільне
. Оберемо довільне  і розглянемо довільну послідовність
і розглянемо довільну послідовність  значень аргументу
значень аргументу  таку, що
таку, що  . Тоді для цього
. Тоді для цього 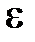 знайдеться номер
знайдеться номер 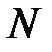 такий, що
такий, що 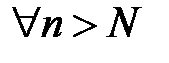 виконано
виконано 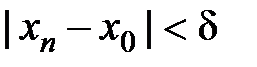 . А тоді
. А тоді 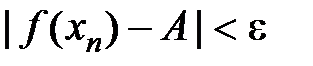 . Таким чином вийшло, що
. Таким чином вийшло, що 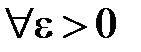
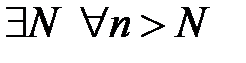 виконано:
виконано:  . Це означає, що
. Це означає, що  , тобто
, тобто  є границею функції
є границею функції 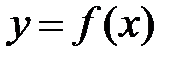 в сенсі Коші. Припустимо, що це не так. Тоді
в сенсі Коші. Припустимо, що це не так. Тоді 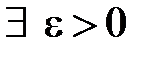
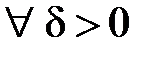 :
: 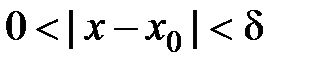
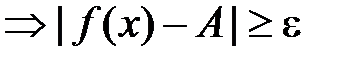 . Побудуємо послідовність
. Побудуємо послідовність  ,
,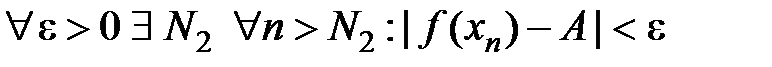 .
.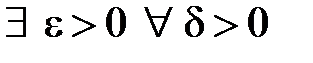 :
:  взяти
взяти  , то отримуємо протиріччя. Отже
, то отримуємо протиріччя. Отже 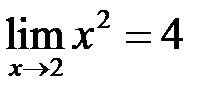 . Використаємо означення Коші. Задамо довільне
. Використаємо означення Коші. Задамо довільне 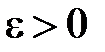 і розглянемо:
і розглянемо: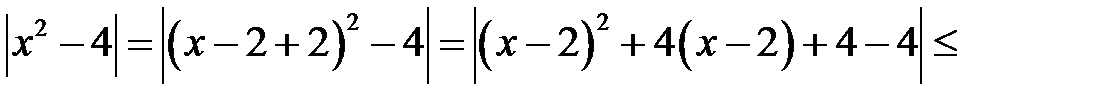
 .
. . Тоді
. Тоді 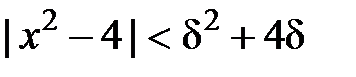 . Вимагатимемо, щоб останній вираз був менше, ніж
. Вимагатимемо, щоб останній вираз був менше, ніж 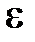 (тоді
(тоді 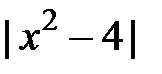 тим більш буде менше, ніж
тим більш буде менше, ніж  ), тобто
), тобто 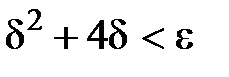 . Розв’язком цієї квадратної нерівності (враховуючи, що
. Розв’язком цієї квадратної нерівності (враховуючи, що 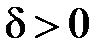 ) є інтервал
) є інтервал  . Таким чином, якщо ми оберемо
. Таким чином, якщо ми оберемо 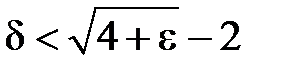 (тобто за заданим
(тобто за заданим  знайшли
знайшли 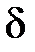 ), то забезпечимо виконання нерівності
), то забезпечимо виконання нерівності 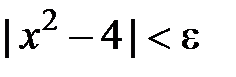 . У якості
. У якості 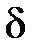 можна взяти будь яке число з інтервалу
можна взяти будь яке число з інтервалу 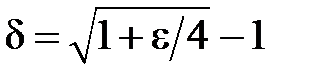 .
.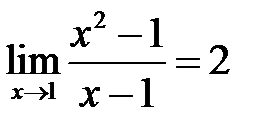 .
.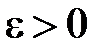 і розглянемо
і розглянемо  :
: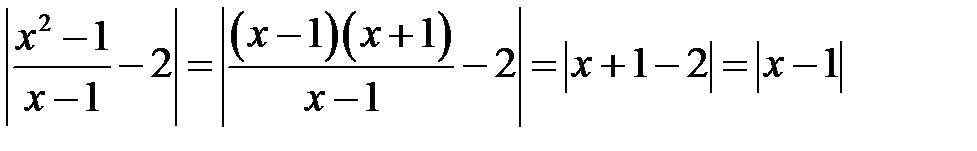 .
.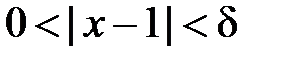 , то, обираючи
, то, обираючи  (наприклад
(наприклад 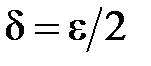 ), забезпечуємо виконання нерівності
), забезпечуємо виконання нерівності  , що й треба було встановити.
, що й треба було встановити. не має ніякої границі при
не має ніякої границі при 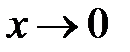 . Скористаємось тепер означенням Гейне. Розглянемо послідовність
. Скористаємось тепер означенням Гейне. Розглянемо послідовність  , де
, де 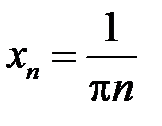 . Очевидно, що
. Очевидно, що 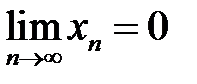 . В той же час:
. В той же час:  .
.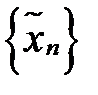 , де
, де  . Знову
. Знову  . Але цього разу
. Але цього разу  .
.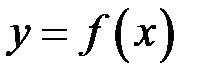 у точці
у точці 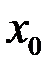 і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було
і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було 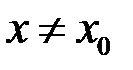 ; або, що те ж саме,
; або, що те ж саме, 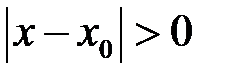 . Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці
. Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці 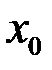 , Але, навіть у тому випадку, коли функція визначена у точці
, Але, навіть у тому випадку, коли функція визначена у точці  , її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з п.8.
, її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з п.8.
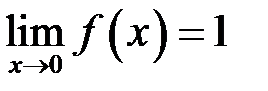 . Задамо
. Задамо 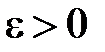 і розглянемо для будь яких
і розглянемо для будь яких 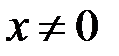 :
: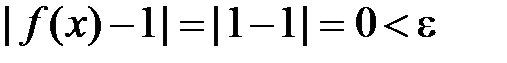 тобто у якості
тобто у якості  можна взяти будь яке додатне число. Разом з цим
можна взяти будь яке додатне число. Разом з цим  .
.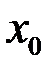 , а границі функції у цій точці не існує. Розглянемо, наприклад, функцію:
, а границі функції у цій точці не існує. Розглянемо, наприклад, функцію: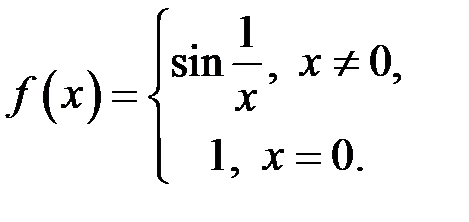
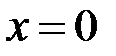 , а границі у цій точці не існує (див. приклад 3).
, а границі у цій точці не існує (див. приклад 3).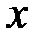 прямувало до скінченого числа
прямувало до скінченого числа 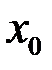 . Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид:
. Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид: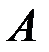 називається границею функції
називається границею функції 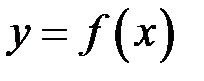 при
при 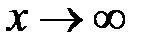 , якщо для будь якого числа
, якщо для будь якого числа 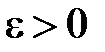 існує таке число
існує таке число 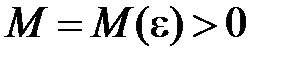 , що з нерівності
, що з нерівності 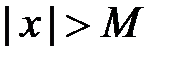 випливає нерівність
випливає нерівність 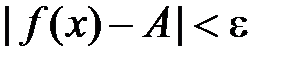 .
.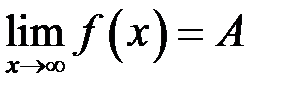 .
. при
при 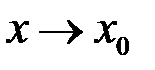 дорівнює нескінченності, якщо для будь якого додатного числа
дорівнює нескінченності, якщо для будь якого додатного числа  існує таке додатне число
існує таке додатне число 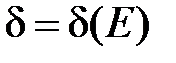 , що виконання з нерівності
, що виконання з нерівності 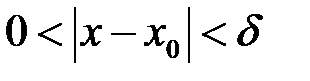 випливає нерівність
випливає нерівність 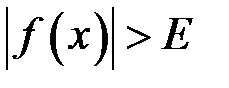 .
.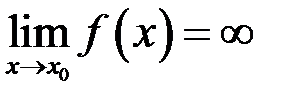 .
.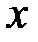 до числа
до числа 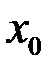 значення функції
значення функції 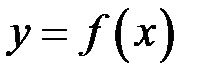 може бути зроблено за модулем більшим, ніж будь яке наперед задане число
може бути зроблено за модулем більшим, ніж будь яке наперед задане число 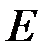 .
.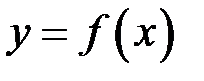 називається нескінченно великою у точці
називається нескінченно великою у точці 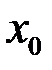 .
. є нескінченно великою у точці
є нескінченно великою у точці  .
.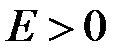 і розглянемо:
і розглянемо: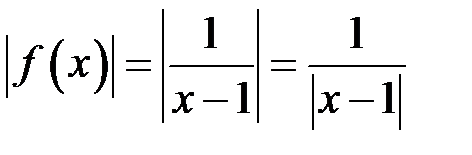 .
. , то
, то  . Вимагатимемо, щоб
. Вимагатимемо, щоб 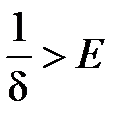 , тобто
, тобто 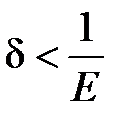 . Наприклад, можна взяти
. Наприклад, можна взяти  . Тоді за даним
. Тоді за даним 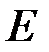 ми знайшли
ми знайшли 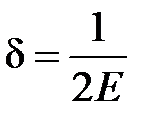 таке, що з нерівності
таке, що з нерівності 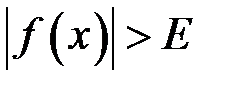 , тобто
, тобто 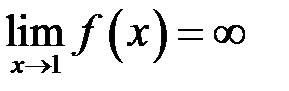 .
.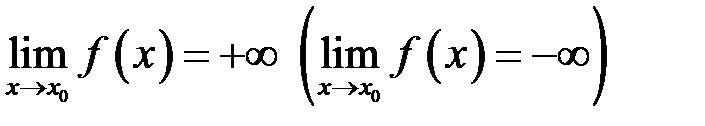 , якщо
, якщо 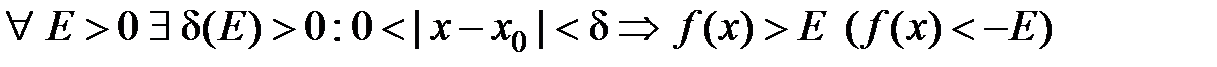 .
. .
. має нескінченну границю при
має нескінченну границю при 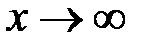 , тобто
, тобто  .
. називається границею зліва функції
називається границею зліва функції 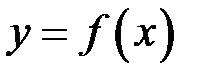 при
при 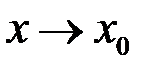 , якщо
, якщо 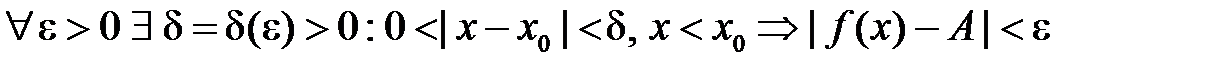 .
.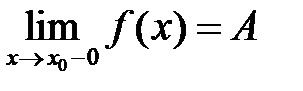 .
. називається границею справа функції
називається границею справа функції 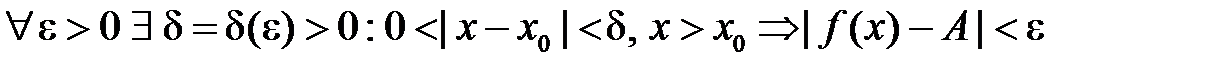 .
. .
.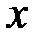 прямує до
прямує до 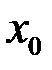 , залишаючись весь час меншим, ніж
, залишаючись весь час меншим, ніж  , а у другому означенні – залишаючись весь час більшим, ніж
, а у другому означенні – залишаючись весь час більшим, ніж 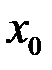 . Границі справа і зліва функції
. Границі справа і зліва функції  у точці
у точці 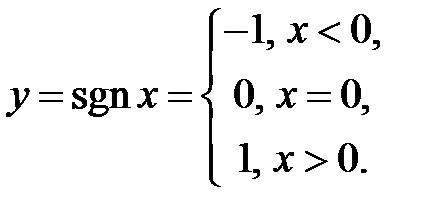
 . Спочатку розглянемо випадок
. Спочатку розглянемо випадок 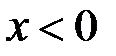 . Задамо довільне
. Задамо довільне 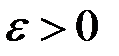 і за цим
і за цим 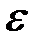 знайдемо
знайдемо 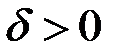 таке, що з нерівності
таке, що з нерівності 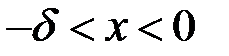 буде випливати нерівність
буде випливати нерівність 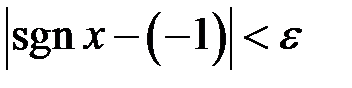 . Дійсно, якщо
. Дійсно, якщо 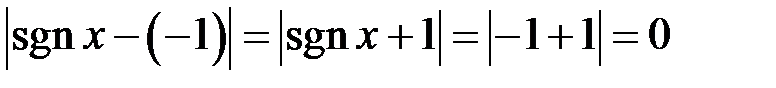 , тобто у якості
, тобто у якості 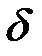 можна взяти будь яке додатне число. Таким чином
можна взяти будь яке додатне число. Таким чином 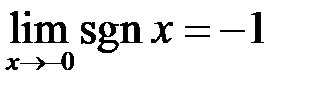 . Аналогічно показуємо, що
. Аналогічно показуємо, що 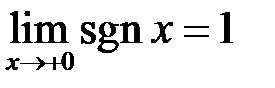 .
.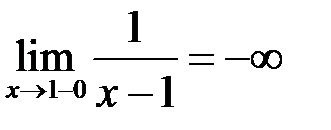 , а
, а 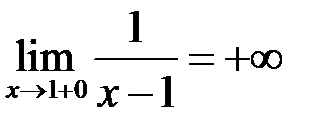 .
. . Задамо довільне
. Задамо довільне  і покажемо, що існує таке
і покажемо, що існує таке  , що з нерівності
, що з нерівності  буде випливати
буде випливати 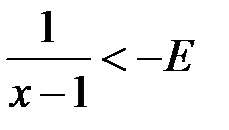 . Дійсно, оскільки
. Дійсно, оскільки 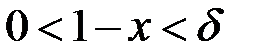 , то
, то 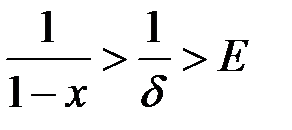 , якщо тільки
, якщо тільки 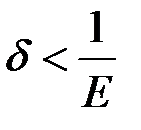 . А звідси випливає, що
. А звідси випливає, що  , що й треба було встановити. Аналогічно доводиться, що
, що й треба було встановити. Аналогічно доводиться, що  .
.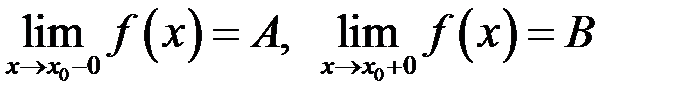 , геометрично ілюструється на рис. 39.
, геометрично ілюструється на рис. 39.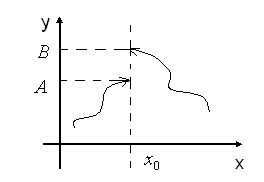
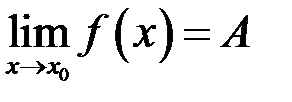 має місце тоді і тільки тоді, коли у точці
має місце тоді і тільки тоді, коли у точці  існують однобічні границі, і вони дорівнюють
існують однобічні границі, і вони дорівнюють 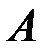 .
.

 . Це означає, що нерівність
. Це означає, що нерівність 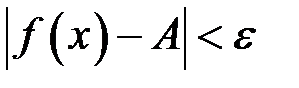 справджується як для
справджується як для 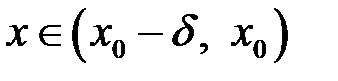 , так і для
, так і для 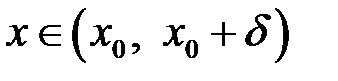 . А це згідно означенню однобічних границь означає, що
. А це згідно означенню однобічних границь означає, що 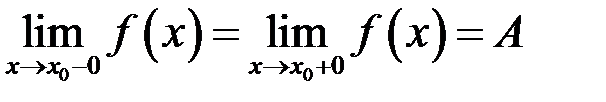 .
.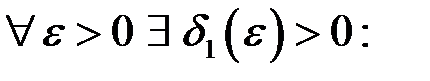
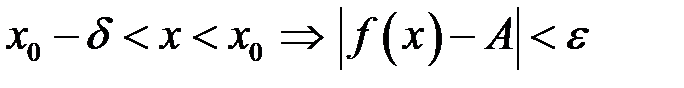 . А також
. А також 
 . Візьмемо
. Візьмемо 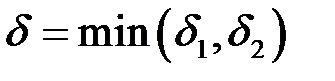 . Тоді якщо
. Тоді якщо 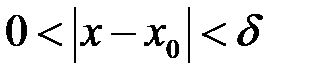 , то буде виконана нерівність
, то буде виконана нерівність 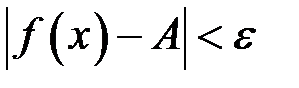 , що й означає, що
, що й означає, що 


