
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометричні функції подвійного аргументуСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Синус подвійного аргументу:
Косинус подвійного аргументу:
Наслідки: 1)
2)
Тангенс подвійного аргументу:
Формулами зведення називають формули, що виражають тригонометричні функції від аргументів ( Правила написання формул зведення: 1) а) для аргументів б) для аргументів 2) перед отриманою функцією стоїть той знак, який має вихідна функція. Приклад: 1) 2) 3) 4)
14. Найпростіші тригонометричні рівняння. Розв’язання рівняння
15. Найпростіші тригонометричні рівняння. Розв’язання рівняння
16. Найпростіші тригонометричні рівняння. Розв’язання рівняння
Поняття похідної, її геометричний та фізичний зміст
Фізичний зміст похідної.
Сприймання і усвідомлення поняття дотичної до кривої. Для введення означення дотичної до кривої розглянемо функцію y=f(x) і її графік криву лінію. Нехай точки А і М належать графіку функції y=f(x), проведемо січну АМ.
Означення: Дотичною АТ до графіка функції y=f(x) в точці А називається граничне положення січної АМ, коли точка М, рухаючись по кривій, наближається до точки А Дотична –це пряма, а положення прямої
Отже, провести дотичну до графіка означає знайти число к. Нехай в точці А(x 1) Надамо аргументу x 2) Знайдемо відповідний приріст функції: 3) Складемо відношення Із трикутника АМК маємо: 4) Якщо Отже, Знаходження кута Рівняння дотичної:
Поняття похідної. Правила диференціювання. Похідні основних елементарних функцій
Правила диференціювання. 1) Теорема: Якщо функції f(x) і g(x) диференційовані в точці х, то їхня сума диференційована в цій точці і (f(x)+g(x))'=f '(x)+g'(x) або коротко говорять: похідна суми дорівнює сумі похідних. Доведення: Розглянемо функцію у = f(x) + g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки а) Похідна різниці дорівнює різниці похідних. Нехай у(х) = f(x) - g(x), тоді f(x) = y(x) + g(x) і f'(x) = у`(х) + g'(x), звідси у`(х) = f '(x) - g'(x). б) Похідна суми декількох функцій дорівнює сумі похідних цих функцій, тобто
Приклад. Знайдіть похідні функцій
2) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х, то їхній добуток також — диференційована функція в цій точці і (f(x) • g(x))' = f ' (x) • g(x) + f(x) • g'(x), або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції. Доведення: Розглянемо функцію у = f(x)g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки | а) Постійний множник можна винести за знак похідної:
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
Приклад. Знайдіть похідні функцій:
3) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і
Доведення: Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Похідна елементарних функції:
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |











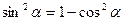





 13. Формули зведення
13. Формули зведення


 ) через функції від аргументу a.
) через функції від аргументу a. назва функції вихідної не змінюється
назва функції вихідної не змінюється назву вихідної функції змінюється на ко-функцію
назву вихідної функції змінюється на ко-функцію



 та окремі випадки.
та окремі випадки.
 та окремі випадки.
та окремі випадки.
 та окремі випадки.
та окремі випадки.



 Зафіксуємо точку А. Нехай точка М, рухаючись по кривій, наближається до точки А. При цьому січна АМ буде повертатись навколо точки А і в граничному положенні при наближенні точки М до точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А.
Зафіксуємо точку А. Нехай точка М, рухаючись по кривій, наближається до точки А. При цьому січна АМ буде повертатись навколо точки А і в граничному положенні при наближенні точки М до точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А. , яка проходить через точку A(x
, яка проходить через точку A(x  ;y
;y  , де
, де  - кут між прямою і додатнім напрямом осі ОХ.
- кут між прямою і додатнім напрямом осі ОХ.
 одержимо нове значення аргументу
одержимо нове значення аргументу 


 . Так як
. Так як  - куту нахилу січної АМ з додатним напрямом осі ОХ, то
- куту нахилу січної АМ з додатним напрямом осі ОХ, то  .
. , то
, то  і точка М буде переміщуватись по кривій, наближуючись до точки А. При цьому січна АМ буде повертатись навколо точки А, а величина кута
і точка М буде переміщуватись по кривій, наближуючись до точки А. При цьому січна АМ буде повертатись навколо точки А, а величина кута  буде змінюватись зі зміною
буде змінюватись зі зміною  - кутовий коефіцієнт дотичної.
- кутовий коефіцієнт дотичної. дотичної до графіка функції в точці з абсцисою
дотичної до графіка функції в точці з абсцисою  і кутовому коефіцієнту дотичної.
і кутовому коефіцієнту дотичної.

 х. Тоді
х. Тоді
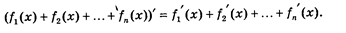







 Нехай у(х)=
Нехай у(х)=  , тоді f(x) = у(х) • g(x). Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, f'(x) = у'(х) • g(x) + у(х) • g'(x). Виразимо з цією формули у'(х):
, тоді f(x) = у(х) • g(x). Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, f'(x) = у'(х) • g(x) + у(х) • g'(x). Виразимо з цією формули у'(х):





