
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Границя послідовності. Границя функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нагадаємо, що закон, за яким кожному натуральному числу Означення 1. Число
або скорочено:
Якщо число Наприклад, послідовність Справді, розглянемо різницю
Тепер для як завгодно малого
Оскільки Означення границі для послідовності, як для функції натурального (дискретного) аргумента, легко перенести і на функцію неперервного аргумента. Означення 2. Число
Ця границя Границю функції можна означити безпосередньо, не користуючись границею послідовності. Означення 3. Число
тобто
Означення 3 границі функції можна замінити більш спрощеним, яке на перших порах легше запам’ятовується. Означення 4. Число
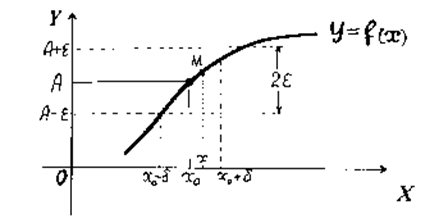
Вияснимо геометричний зміст означення 3, скориставшись графіком функції (див. рис.21)
Рис. 21
Припустимо, що при Можна довести, що означення 2 і 3 є еквівалентними. Означення 2 зручно застосовувати для функцій, границя яких в даному процесі не існує. Розглянемо, наприклад, функцію а) б) в) Отже, для наведених збіжних до нуля послідовностей функція
Рис. 22
Графік функції Означення 5. Число
Таким чином співвідношення
залишається правильним і в тому випадку, коли
Властивості границь
Теорема 1. Якщо функцію
то
Навпаки, якщо
Дійсно, нехай Навпаки, нехай виконується рівність (2). А це означає, що для
Наслідок. Якщо Дійсно, за теоремою 1 маємо Теорема 2. Нехай існують скінченні границі
Доведемо, наприклад, другу рівність. За теоремою 1(формула 1) з того, що Рівності перша і третя теореми 2 доводяться аналогічно. Наслідок. Сталий множник можна виносити за знак границі, тобто якщо
оскільки Означення 1. Функція Означення 2. Функція Теорема 3. Якщо границя Доведення дамо, коли
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.142.218 (0.01 с.) |

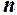 ставиться у відповідність число
ставиться у відповідність число 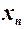 , визначає функцію натурального аргумента
, визначає функцію натурального аргумента 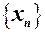 .
.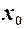 називається границею послідовності
називається границею послідовності  (позначається
(позначається  ), якщо для довільного
), якщо для довільного  існує номер
існує номер 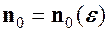 , що залежить від
, що залежить від 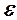 , такий, що для всіх наступних номерів
, такий, що для всіх наступних номерів 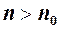 виконується нерівність
виконується нерівність ,
, (14)
(14)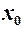 є границею послідовнсті
є границею послідовнсті  , то ще прийнято говорити, що послідовність
, то ще прийнято говорити, що послідовність 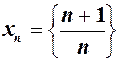 має своєю границею число
має своєю границею число 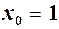 , тобто
, тобто 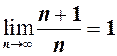 .
.
 , наприклад,
, наприклад, 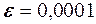 , можна підібрати номер
, можна підібрати номер 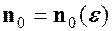 , що залежить від
, що залежить від  . Отже, якщо взяти
. Отже, якщо взяти 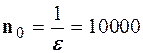 , то тепер для всіх номерів
, то тепер для всіх номерів  маємо
маємо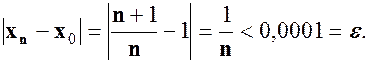
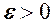 можна вибирати як завгодно малим, то число
можна вибирати як завгодно малим, то число 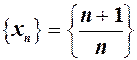 при
при  при
при 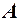 називається границею функції
називається границею функції  в точці
в точці  існує і дорівнює
існує і дорівнює 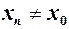 для всіх
для всіх  .
.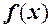 .
.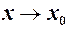 , якщо
, якщо  , що залежить від
, що залежить від 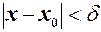 випливає нерівність
випливає нерівність  , позначається
, позначається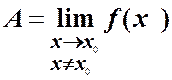 ,
, (15)
(15) називається границею функції
називається границею функції  при
при 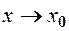 , якщо
, якщо 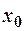 , за винятком, можливо, самої точки
, за винятком, можливо, самої точки 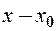 нескінченно мала випливає, що різниця
нескінченно мала випливає, що різниця  теж нескінченно мала, тобто
теж нескінченно мала, тобто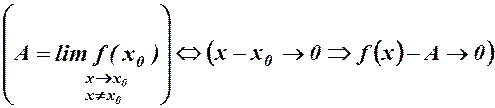 (16)
(16)
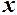 прямуючому до
прямуючому до 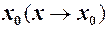 , функція
, функція 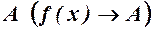 , тобто
, тобто 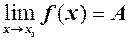 . Згідно означення 3 це значить, що для як завгодно малого
. Згідно означення 3 це значить, що для як завгодно малого 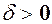 таке, що із нерівності
таке, що із нерівності  нерівність
нерівність 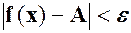 . Це означає, що для всіх
. Це означає, що для всіх 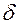 , відповідні точки
, відповідні точки 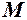 графіка функції
графіка функції  , обмежену прямими
, обмежену прямими 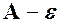 і
і 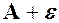 .
. при
при 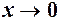 . Ця функція визначена для всіх значень
. Ця функція визначена для всіх значень  , є парною, її графік симетричний відносно осі
, є парною, її графік симетричний відносно осі  . Вияснимо поведінку функції
. Вияснимо поведінку функції 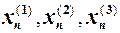 збіжних до
збіжних до 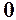 при
при  тоді
тоді 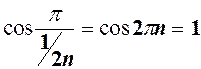 для
для 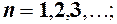
 тоді
тоді 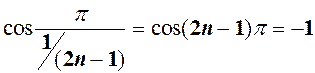 для
для  тоді
тоді  для
для 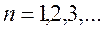 .
. не існує (див. частину графіка на рис. 22)
не існує (див. частину графіка на рис. 22)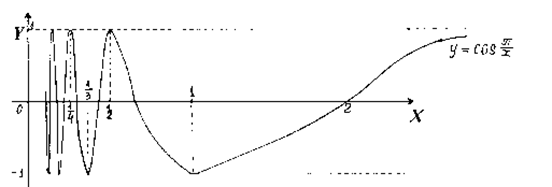
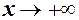 або
або  , якщо для як завгодно малого
, якщо для як завгодно малого 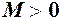 таке, що із нерівності
таке, що із нерівності 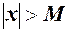 випливає нерівність
випливає нерівність 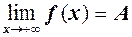 , або
, або 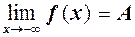 , або
, або  .
.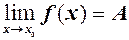
 або
або  .
. , тобто
, тобто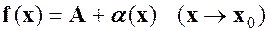 , (1)
, (1)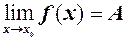 (
(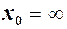 ). (2)
). (2)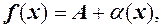 де
де  н.м. при
н.м. при  де
де 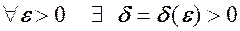 таке, що із нерівності
таке, що із нерівності  нерівність
нерівність 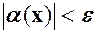 , або
, або 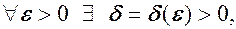 таке, що із
таке, що із 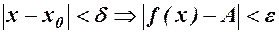 Позначимо
Позначимо 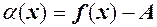 , тоді остання нерівність означає, що
, тоді остання нерівність означає, що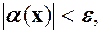 тобто н.м.
тобто н.м.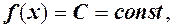 то
то 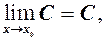 тобто границя сталої величини дорівнює цій сталій.
тобто границя сталої величини дорівнює цій сталій.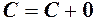 або
або 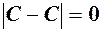 буде меншою
буде меншою 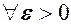 .
.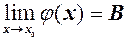 .Тоді
.Тоді 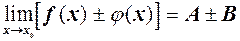 ,
, 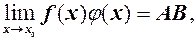
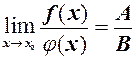 за умови, що
за умови, що 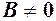 .
.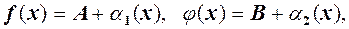 де
де 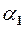 і
і 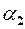 – н.м. при
– н.м. при  н.м. За теоремою 1 маємо, що число
н.м. За теоремою 1 маємо, що число 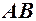 є границею функції
є границею функції 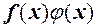 при
при 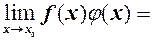

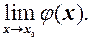
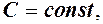 то
то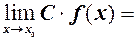

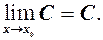
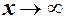 , якщо існує число
, якщо існує число 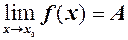 є скінченною, то функція
є скінченною, то функція 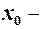 скінченне. Із рівності
скінченне. Із рівності 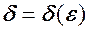 таке, що із
таке, що із 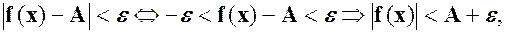 тобто
тобто 


