
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова довірчих границь і інтервалів.Содержание книги
Поиск на нашем сайте
Для побудови довірчого інтервалу (чи границі) необхідно знати закон розподілу статистики z=z (x1,...,xn), по якій оцінюється невідомий параметр (такою статистикою може бути оцінка z = â (x1,...,xn)). Один зі способів побудови полягає в наступному. Припустимо, що деяка випадкова величина j = j(z, a), що залежить від статистики z і невідомого параметра a така, що 1) закон розподілу 2) j(z, a) є неперервною та монотонною по Виберемо діапазон для P{ f1 £ j(z, a) £ f2 } ³ PД, (3.1) для чого досить у якості P{ g(z, f1) £ a £ g(z, f2) } ³ PД. Це співвідношення вірне при будь-якім значенні параметра a (оскільки це так для (1)), і тому, відповідно до визначення, випадковий інтервал (g (z, f1), g (z, f2)) є довірчим для a з рівнем довіри РД. Якщо Для побудови однобічної границі для a виберемо значення P{ j(z, a) ³ f1 }³ PД, f1=Q (1 - PД) чи P{ j(z, a) £ f2 }³ PД , f2 = Q (PД), де Приклад 3.3. Довірчий інтервал з рівнем довіри РД для середнього a нормальної сукупності при відомій дисперсії s 2. Нехай x Введемо її нумерацію, утворивши випадкову величину
яка розподілена нормально N (0, 1)при будь-якім значенні а. По заданому рівні довіри РД визначимо для j відрізок [- fp, fp ] так, щоб
тобто fp - квантиль порядку (1+ РД)/2 розподілу N (0,1); помітимо, що j залежить від а, але (3.3) вірно при будь-якім значенні а. Підставимо в (3.3) виразу для j з(3.2) і розв’язуючи нерівність під знаком ймовірності в (3.3) відносно а; одержимо співвідношення
виконується при будь-якім значенні а. Під знаком імовірності дві функції спостережень
визначають випадковий інтервал I (x1,..., xn) =(a1 (x1,..., xn), a2 (x1,..., xn)), (3.5a) який у силу (3.4) накриває невідоме значення параметра а з великою імовірністю РД при будь-якому значенні а, і тому, по визначенню довірчого інтервалу, він є довірчим з рівнем довіри РД.
У загальному випадку випадкову величину j у (1) можна побудувати таким чином. Визначимо функцію розподілу F (z / a)статистики z (F, звичайно, залежить від а). Для неперервної z випадкова величина j (z, а) º F(z / a),як неважко бачити, розподілена рівномірно на відрізку [0, 1] при будь-якім значенні а; прийнявши f1= (1- PД)/ 2, f2 = (1+PД)/ 2, будемо мати (3.4) у вигляді P{f1 £ F (z / a) £ f 2} = PД. Для дискретної z ситуація аналогічна. Можна міркувати інакше: при будь-якому фіксованому значенні а визначимо відрізок [ z 1(a), z 2(a)] так, що P{ z1 (a)£ z £ z2 (a)} ³ РД; (3.6) ясно, що в якості z1 і z2 можна взяти квантилі, тобто визначити з умов F (z !/ a)=(1- РД)/ 2, F (z 2/ a)=(1+ РД)/ 2. Якщо z1 (a) і z2 (a) монотонно зростають по а, то, розв’язуючи дві нерівності під знаком Р в (3.6) і беручи до уваги те, що z 1(a) < z 2(a),одержимо: P{ z 2-1(z) £ a £ z1-1(z) } ³ РД , є вірним при будь-якому а; ясно, що інтервал (z2-1 (z), z1-1 (z)), обумовлений двома функціями від z, є довірчим з рівнем довіри Р Д. Рівень довіри. Рівень довіри РД означає, що правило визначення інтервалу дає вірний результат з імовірністю РД, що звичайно вибирається близькою до 1, однак, 1 не дорівнює. Переконаємося статистично на прикладі в тім, що довірчий інтервал з рівнем довіри РД може не містити (з малою імовірністю 1- РД) істинне значення параметру. Приклад 3.4. Розглянемо наведений у (3.5) випадковий інтервал I(x1,..., xn), що при будь-якім значенні а накриває це значення з великою імовірністю РД: Р { I (x1,...,xn) є a } = Р Д, і тому, якщо знехтувати можливістю здійснення події a Ï I, що має малу імовірність (1- РД), можна вважати подія a Î I(x1,...,xn) є практично достовірною, тобто можна вірити тому, що обчислений за конкретними спостереженнями x1,...,xn інтервал I містить невідоме значення параметра а. Проведемо випробування інтервалу (3.5) на 50 вибірках обсягу n= 10 для трьох рівнів довіри Р Д: 0.9, 0.99, 0.999 (відповідно, три значення fp). При Р Д = 0.9 число невірних з k =50 результатів виявиться в околиці 5, тому що середнє число невірних k (1- Р Д) = 5. При Р Д =0.99 поява хоча б одна невірного з k =50 досить ймовірна: імовірність цієї події 1- Р Д k=1-0.9950» 0.61. При Р Д =0.999 поява хоча б одна невірного є сумнівною: імовірність цієї події 1- Р Д k=1-0.99950» 0.05.
3.3. Завдання для самостійної роботи 1. Визначити, скільки разів з k =50 довірчий інтервал виявився невірним; Це зробимо для трьох значень Р Д. Графіки для Р Д =0.9 і Р Д =0.99 роздрукувати. 2. Провести аналогічно 50 випробувань довірчого інтервалу (3.7) - (3.9) для випадку невідомої дисперсії. Інтервали для параметрів нормального розподілу. Нехай х1, …,хn - вибірка з нормального N(a,s2) розподілу; значення середнього а і дисперсії s2 невідомі. Оцінки для а і s2 мають вигляд:
Як відомо, довірчим інтервалом для середнього а з рівнем довіри Р Д при невідомій дисперсії є інтервал I (x) = (a1 (х), a2 (х)), (3.8) де tp - квантиль порядку (1+ Р Д)/2 розподілу Стьюдента з n-1 ступенями волі. Довірчим інтервалом для стандартного відхилення s з рівнем довіри Р Д є інтервал I (x) = (s1 (х), s2 (х)), (3.10) де тут t1 і t2 - квантилі порядків відповідно (1+ Р Д)/2 і (1- РД)/2 розподілу хі-квадрат з n-1 ступенями волі. Читачеві пропонується самостійно згенерувати вибірку обсягу n=20 з нормального розподілу з параметрами a = 10, s2= 22=4 і визначити довірчі інтервали для a і s з рівнем довіри Р Д: 0.8, 0.9, 0.95, 0.98, 0.99, 0.995, 0.998, 0.999. Результати виписати у вигляді таблиці. Зі зростанням Р Д інтервал розширюється, зі зростанням n - зменшується. Якщо нас цікавлять не інтервали, а верхні чи нижні довірчі границі, то, як відомо, вони визначаються тими ж формулами (3.9) та (3.11), однак значення порогових значень t змінюються. Наприклад, нижньою довірчою границею для a з рівнем довіри Р Д є значення
де tp - квантиль порядку Р Д розподілу Стьюдента з n-1 ступенями волі, а верхньою границею для s з рівнем довіри Р Д є
де t2 - квантиль порядку 1- Р Д розподілу хі-квадрат з n-1 ступенями волі. Завдання: визначити верхні довірчі границі для а і s з рівнем довіри Р Д = 0.95. 1) для заданої задачі побудувати оцінку заданим методом (варіанти завдань див. нижче); 2) побудувати довірчий інтервал, заснований на цій оцінці; 3) згенерувати вибірку заданого обсягу; 4) обчислити довірчий інтервал.
Звіт по роботі повинен містити: постановки питань, формули, графіки випробування довірчого інтервалу для двох випадків: з відомою і невідомою дисперсією (по п. 1.2), таблицю довірчих інтервалів для різних РД (по п. 1.3), вивод формул для оцінок і інтервалів, згенеровану вибірку й обчислений інтервал (по п. 1.4). Варіанти. Задача 1. Відстань а до деякого об'єкта вимірялася n1 раз одним приладом і n2- другим; результати х1,…,хn1; y1,…,yn2... Обидва прилади при кожнім вимірі дають незалежні випадкові похибки, нормально розподілені із середнім 0 і стандартними відхиленнями s1 і s2 відповідно. Методом максимальної правдоподібності побудувати оцінку â для а і довірчий інтервал з рівнем довіри РД. Варіанти вихідних даних
Дані вимірювання одержати шляхом генерації випадкових величин з заданими параметрами. Розв’язок (без висновку). Оцінка
довірчий інтервал I=( де
Задача 2. Виготовлено велику партію з N =10000 приладів. Відомо, що час безвідмовної роботи випадково і розподілено за експоненційним законом з щільністю
З метою визначення значення параметра а цієї партії були поставлені на іспити n приладів; часи безвідмовної роботи виявилися рівними х1,…,хn. Методом моментів побудувати оцінку для а і довірчий інтервал з рівнем довіри РД. Крім того, побудувати довірчий інтервал для числа М приладів, що мають час безвідмовної роботи менш 50 годин. Варіанти вихідних даних
Дані вимірювання одержати шляхом генерації випадкових величин з заданими параметрами. Розв’язок(без висновку). Оцінка
довірчий інтервал для а Ia = ( де t1=Q (2n, (1- РД)/ 2), t2=Q (2n, (1+РД)/ 2) - квантилі розподілу хі-квадрат з 2n ступенями волі; довірчий інтервал для М IM = (N (1- exp (- Приклад 3.5. Деяка невідома відстань а вимірялося з адитивною випадковою помилкою e, розподіленої за законом Коші з щільністю p e (x) = За результатами х1,…,хn незалежних вимірів методом порядкових статистик побудувати оцінку для а і наближений довірчий інтервал з коефіцієнтом довіри РД. Варіанти вихідних даних
Дані вимірювання одержати шляхом генерації випадкових величин з заданими параметрами. Розв’язок(без висновку). Оцінкою для а є вибіркова медіана - порядкова статистика з номером[ n/2 ] + 1
або (у цих статистик асимптотичні властивості однакові). Наближений довірчий інтервал, заснований на асимптотичному розподілі вибіркової р-квантилі I =( де tp=Q((1+РД)/2) - квантиль порядку (1+ РД)/2 розподілу N(0,1).
Задача 4. У водоймі живе деяка біологічна популяція, що складається із суміші істот двох віків. Довжина істоти - випадкова величина, розподілена по нормальному законі N(ai, si2 ), де i=1,2 - індекс, що відноситься до віку. З метою визначення частки q істот 1-го віку проведений вилов n істот і обмірюваний їхня довжина. За результатами х1,…,хn методом моментів побудувати оцінку Варіанти вихідних даних
Прийняти s1=1див, s2=1див. Виміру одержати моделюванням із заданим значенням q. Розв’язок(без висновку): I = (q1, q2 ),
an º tp - квантиль порядку (1+ РД)/ 2 для N (0,1).
В Варіаційним рядом називається така послідовність елементів вибірки
Випадкова величина X має розподіл Пуассона, якщоїї можливізначення 0, 1, 2, …m складають нескінченну, але лічильну множину, а відповідні ймовірності задаються наступною формулою з параметром а, який має зміст інтенсивності потоку, …. Який з перелічених виразів правильно закінчує означення?
Випадкова величина X має експоненціальний розподіл, якщоїї Д Дана вибірка X 1, X 2, …, Xn об’єму n з параметричного сімейства розподілів ℱq, qÎQ. Яка з перелічених формул не підходить для визначення оцінки параметра q* за k- ммоментом?
Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з функцій
Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з оцінок
Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з оцінок
Для одної з вибірок отримані чотири різних незміщених оцінки невідомого параметру 1,12; 1.08; 1.23; 1.11, які представляють собою випадкові величини з відповідними дисперсіями 0,28; 0.30; 0.32; 0.26. Яка з оцінок є найбільш достовірною? 1,23 Для кожної з чотирьох різних вибірок отримані оцінки, що мають наступні дисперсії 0,28; 0.30; 0.32; 0.26 і відповідні зміщення 0,5; 0,3; 0,3; 0,4. Знайти середній квадрат помилки для кожної з оцінок. Оцінка з яким порядковим номером є найкращою? 2 Для вибірки з рівномірного розподілу U0,θ об’ємом n обчислені середні квадрати помилок Eθ (q* - θ)2 і Eθ (
Для визначення квантілі розподілу застосовується його …. Яке з перелічених тверджень правильно продовжує речення?
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
Для нормального розподілу з математичним очікуванням а і дисперсією
З За вибіркою Xi, i= 1, …, n з розподілу ℱ, яка має безперервну функцію розподілу f,створена гістограма, що має k інтервалів, на яких побудовані прямокутники довжиною lj та висотою fj. Кожен з інтервалів Аj містить vj елементів вибірки. При п
Н Нехай Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу ℱ з функцією розподілу F. Нехай Fn* - емпіричнафункція розподілу, що побудована за цією вибіркою. Тоді для будь-якого yÎ R …
Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу ℱ з функцією розподілу F. Нехай Fn* - емпіричнафункція розподілу, що побудована за цією вибіркою. Тоді для будь-якого yÎ R …
Нижче подано доведення незміщенності оцінки для першого моменту вибірки X 1, X 2, …, Xn (Лема 1). Який з шості знаків рівності, якщо рахувати їх зліва направо, є хибним в цьому доведенні? Нижче подано доведення відомої формули для дисперсії: «дисперсія рівна середньому квадрату мінус квадрат середнього». Який з чотирьох знаків рівності, якщо рахувати їх зліва направо, є хибним в цьому доведенні? На автоматичну телефонну станцію поступає простішій потік викликів з інтенсивністю 0,8 викл/хв. Знайти ймовірність того, що на протязі 2-х хвилин на станцію не поступить жодного виклику. До якого з перелічених чисел найбільш наближена визначена ймовірність? 0,6 Нехай 0.123, 0.248, 0.366, 0.63, 0.207 є вибіркою об’єму 5 з рівномірного розподілу U0,θ Знайти оцінку верхньої межі розподілу θ* за першим моментом. До якого з перелічених нижче чисел найбільш наближена визначена оцінка?
Нехай 0.123, 0.248, 0.366, 0.63, 0.207 є вибіркою об’єму 5 з рівномірного розподілу U0,θ Знайти оцінку верхньої межі розподілу θ* за першим моментом. Чи є знайдена оцінка незміщеною? Так Нехай 0.123, 0.248, 0.366, 0.63, 0.207 є вибіркою об’єму 5 з рівномірного розподілу U0,θ Знайти оцінку верхньої межі розподілу θ* за першим моментом. Чи є знайдена оцінка змістовною? Так Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти оцінку математичного очікування a* розподілу за першим моментом. До якого з перелічених нижче чисел найбільш наближена визначена оцінка?
Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти оцінку математичного очікування a* розподілу за першим моментом. Чи є знайдена оцінка незміщеною? Так Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти оцінку математичного очікування a* розподілу за першим моментом. Чи є знайдена оцінка змістовною? Так Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти зміщену оцінку дисперсії
Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти зміщену оцінку дисперсії Так Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти незміщену оцінку дисперсії S02 розподілу за першим моментом. До якого з перелічених нижче чисел найбільш наближена визначена оцінка?
Нехай 2.083, 1.992, 1.914, 2.234, 2.256 є вибіркою об’єму 5 з нормального розподілу Na,2 Знайти незміщену оцінку дисперсії S02 розподілу за першим моментом. Чи є знайдена оцінка змістовною? Так Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу ℱq, qÎQ з функцією щільності розподілу fq. Метод максимальної правдоподібності полягає у знаходженні такого значення q*, яке відповідає екстремуму … Яким з перелічених варіантів не можна закінчити означення?
Нехай 0, 0, 0, 1, 1 – вибірка об’єму 5 з розподілу Пуассона Нехай 0.969, 0.59, 0.129, 0.863, 0.033 – вибірка об’єму 5 з рівномірного розподілу U0,θ. Знайти оцінку максимальної правдоподібності верхньої межі
Нехай випадкові величини
Нехай X 1, X 2, …, Xn – вибірка об’єму п з розподілу Na,
Нехай 0<p<1, q=1-p, m=0, 1,…, n – цілі невід’ємні числа, а С – біноміальний коефіцієнт. Дискретна випадкова величина Х має біноміальний розподіл, якщо ймовірність отримання нею значення т складає ….Який з перелічених виразів правильно закінчує означення?
Нехай ξ0, ξ1, …, ξk незалежні та мають стандартний нормальний розподіл. Розподіл якої з перелічених випадкових величин називається розподілом Ст’юдента з k ступенями вільності і позначається Tk?
П При λ=1 гама-розподіл
При цілому λ>0 гама-розподіл У Укажіть, яке формулювання леми для вибіркового першого моменту є правильним?
Укажіть, яке формулювання леми для вибіркової дисперсії є правильним?
Укажіть, яке формулювання леми для вибіркового k- го моменту є правильним?
Ф Функція I(Xi < y) = Індикатор події Функція, яка називається індикатором подій, є випадковою функцією, що розподілена …
Функція розподілу для N0,1 є …. Яке з перелічених тверджень правильно продовжує речення?
Я Яка з перелічених задач вирішується за допомогою математичної статистики?
Яка з перелічених властивостей емпіричної функції розподілу Fn* є хибною?
Яка з перелічених властивостей гістограми, побудованої за вибіркою
Який з перелічених варіантів формули Стерджесса, що задає залежність кількості інтервалів k від об’єму вибірки n при побудові гістограми,є хибним?
Яка таблиця з наведеного переліку не містить помилок? Таблиця 1 – Теоретичні та емпіричні моменти Яка з перелічених величин не може бути застосована для порівняння оцінок?
Які з перелічених виразів відповідають означенню точного довірчого інтервалу (θ -, θ+) для параметра θ рівня довіри 1-
Який з перелічених виразів описує щільність нормального розподілу f(x) з математичним очікуванням а і середнім квадратичним відхиленням σ? Яка з перелічених функцій а f(x) називається функцією Лапласа? Яка з перелічених нижче функцій щільності ймовірностей задає гама-розподіл?
Який з перелічених нижче виразів задає гама-функцію?
Яка з наступних формул застосовна для обчислення гама-функції натурального аргументу k?
Якщо ξ? N0,1. то ….Який з наведений виразів правильно закінчує твердження Леми 7?
Якому з перелічених гама-розподілів належить випадкова величина, яка складає суму квадратів k незалежнихвеличин, розподілених за стандартним нормальним законом?
Який з перелічених розподілів називається розподілом χ2 ступеня вільності k і позначається Нk?
Який з розподілів для вибірки об’єму k
1. Яка з перелічених задач вирішується за допомогою математичної статистики? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 відомий і не залежить від a;
відомий і не залежить від a; .
. - інтервал
- інтервал  так, щоб влучення в нього було практично вірогідно:
так, щоб влучення в нього було практично вірогідно: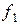 і
і 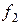 взяти квантилі розподілу
взяти квантилі розподілу  - квантиль рівня
- квантиль рівня  . Після розв’язання нерівності під знаком
. Після розв’язання нерівності під знаком  ,..., xn - вибірка з нормальної N (a, s
,..., xn - вибірка з нормальної N (a, s 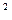 )сукупності. Спроможною оцінкою для а є â = â (x
)сукупності. Спроможною оцінкою для а є â = â (x  ,...,xn) =
,...,xn) =  , розподілена за законом N (a,
, розподілена за законом N (a,  ).
). , (3.2)
, (3.2) , (3.3)
, (3.3) , (3.4)
, (3.4)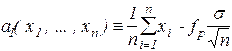 ,
,  (3.5)
(3.5) ,
,  . (3.7)
. (3.7) ,
,  , (3.9)
, (3.9) ,
,  , (3.11)
, (3.11) ,
, ,
,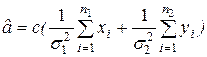 , де з =
, де з =  ;
; ,
,  ),
), - квантиль порядку (1+ РД)/2 розподілу N(0,1).
- квантиль порядку (1+ РД)/2 розподілу N(0,1). , x ³ 0
, x ³ 0 ;
; ,
,  ),
), )), N (1- exp (-
)), N (1- exp (-  ))).
))). , - ¥ < x < ¥.
, - ¥ < x < ¥. ,
,
 ),
),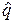 для q і наближений довірчий інтервал з рівнем довіри РД. Побудувати гістограму спостережень.
для q і наближений довірчий інтервал з рівнем довіри РД. Побудувати гістограму спостережень. ,
, ,
,


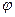 для оцінки параметра
для оцінки параметра  може бути названа статистикою?
може бути названа статистикою?
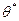 невідомого параметра
невідомого параметра 

 - θ)2 дляоцінок за методом моментів q* та за методом максимальної правдоподібності
- θ)2 дляоцінок за методом моментів q* та за методом максимальної правдоподібності 
 вибірка об’єму п маєвибіркове середнє
вибірка об’єму п маєвибіркове середнє  , вибіркову дисперсію
, вибіркову дисперсію  і незміщену вибіркову дисперсію S02. Яка з перелічених випадкових величин належить до нормального стандартного розподілу?
і незміщену вибіркову дисперсію S02. Яка з перелічених випадкових величин належить до нормального стандартного розподілу?


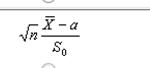
 ?
?


 для будь-якого j= 1,..., k мають місце тільки три з перелічених чотирьох властивостей гістограми. Яка з властивостей є хибною?
для будь-якого j= 1,..., k мають місце тільки три з перелічених чотирьох властивостей гістограми. Яка з властивостей є хибною?
 - випадкова величина, що спостерігається у випадковому експерименті. Нехай після п -разового проведення експерименту в однакових умовах отримані значення випадкової величини X 1, X 2, …, Xn у 1-му, 2-му і т.д. експериментах. Нехай випадкова величина
- випадкова величина, що спостерігається у випадковому експерименті. Нехай після п -разового проведення експерименту в однакових умовах отримані значення випадкової величини X 1, X 2, …, Xn у 1-му, 2-му і т.д. експериментах. Нехай випадкова величина 

 розподілу за першим моментом. До якого з перелічених нижче чисел найбільш наближена визначена оцінка?
розподілу за першим моментом. До якого з перелічених нижче чисел найбільш наближена визначена оцінка?

 . Знайти оцінку максимальної правдоподібності інтенсивності потоку
. Знайти оцінку максимальної правдоподібності інтенсивності потоку  . До якого з перелічених чисел найбільш наближена знайдена інтенсивність? 0,4
. До якого з перелічених чисел найбільш наближена знайдена інтенсивність? 0,4
 і
і  розподілені нормально з математичними очікуваннями a1 і a2 та дисперсіями σ12 і σ22 відповідно. Нехай також g – детермінована змінна величина. Яке з перелічених тверджень є хибним у розумінні стійкості за сумуванням?
розподілені нормально з математичними очікуваннями a1 і a2 та дисперсіями σ12 і σ22 відповідно. Нехай також g – детермінована змінна величина. Яке з перелічених тверджень є хибним у розумінні стійкості за сумуванням?



 перетворюється в …
перетворюється в …



 називається …
називається …


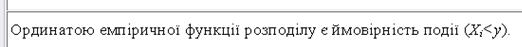


 ?
?






 20 практично співпадає з нормальним?
20 практично співпадає з нормальним?



