Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монету підкидають 10 разів. Знайти ймовірність з’явлення точно 5 гербів. Яке з перелічених чисел найбільш наближається до шуканої ймовірності.Содержание книги
Поиск на нашем сайте
56.1. 0,3
57. Дана наступна вибірка з нормального розподілу: 57.1. 1,0 57.2. 1,5 57.3. 2,0 57.4. 2,5 57.5. 3,0 57.6. 3,5
58. Дана наступна вибірка з нормального розподілу: 64.1 1,0 64.2 1,5 64.3 2,0 64.4 2,5 64.5 3,0 64.6 3,5
59. Дана наступна вибірка з нормального розподілу: 65.1 1,0 65.2 1,5 65.3 2,0 65.4 2,5 65.5 3,0 65.6 3,5
60. Дана наступна вибірка з нормального розподілу: 66.1 1,0 66.2 1,5 66.3 2,0 66.4 2,5 66.5 3,0 66.6 3,5
61. Нехай 0.950, 0.231, 0.606, 0.486, 0.891 є вибіркою об’єму 5 з рівномірного розподілу U0,θ . Знайти оцінку верхньої межі розподілу θ* за першим моментом. 24.1 0,4 24.2 0,5 24.3 0,6 24.4 0,7
62. Нехай 1.1349, -1.3312, 2.2507, 2.5754, -0.2929 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти оцінку математичного очікування a* розподілу за першим моментом. 25.1 1,0 25.2 1.5 25.3 2,0 25.4 2.5
63. Нехай 4.3818, 4.3783, 1.9247, 2.6546, 2.3493 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти зміщену оцінку дисперсії 26.1 0,01 26.2 0,02 26.3 0,03 26.4 0,04
64. Нехай 1.6266, 3.4516, 0.8234, 6.3664, 1.7272 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти незміщену оцінку дисперсії S20 розподілу за першим моментом. 27.1 0,01 27.2 0,02 27.3 0,03 27.4 0,04
65. Нехай 2, 1, 0, 2, 1 – вибірка об’єму 5 з розподілу Пуассона 29.1 0,1 29.2 0,2 29.3 0,3 29.4 0,4
66. Нехай 0.9355, 0.9169, 0.4103, 0.8936, 0.0579 – вибірка об’єму 5 з рівномірного розподілу U0,θ. Знайти оцінку максимальної правдоподібності верхньої межі 30.1 0,6 30.2 0,8 30.3 1,0 30.4 1,2
58. Яка з перелічених задач вирішується за допомогою математичної статистики?
58.1. Відомі результати п’яті вимірювань в однакових умовах одної і тої самої величини, що розподілена нормально. Яким буде найбільш ймовірне значення цієї величини?
59. Нехай 59.1. … якщо X 1, X 2, …, Xn є набором чисел, що є значеннями випадкової величини 59.2. … якщо X 1, X 2, …, Xn є набором з п незалежних і однаково розподілених випадкових величин, що мають, як и 59.3. … якщо розподіл F є повністю невідомим. 59.4. … якщо розподіл F є повністю відомим.
60. Функція називається … 60.1. … індикатором події
61. Функція, яка називається індикатором подій, є випадковою функцією, що розподілена … 61.1. … за законом Бернуллі.
62. Варіаційним рядом називається така послідовність елементів вибірки X 1, X 2, …, Xn, для якої виконується умова … 62.1. … X 1≤ X 2≤ …≤ Xn.
63. Яка з перелічених властивостей емпіричної функції розподілу Fn* є хибною? 63.1. Ординатою емпіричної функції розподілу є ймовірність події (Хі<y).
64. Яка з перелічених властивостей гістограми, побудованої за вибіркою 64.1. Висота прямокутника на Aj складає vj / lj, де lj – довжина інтервалу Aj. 65. Який з перелічених варіантів формули Стерджесса, що задає залежність кількості інтервалів k від об’єму вибірки n при побудові гістограми,є хибним? 65.1. k = 1 + lg2*lg n
66. Яка таблиця з наведеного переліку не містить помилок?
66.1. Таблиця 1 – Теоретичні та емпіричні моменти
66.2. Таблиця 2 – Теоретичні та емпіричні моменти
66.3. Таблиця 3 – Теоретичні та емпіричні моменти
66.4. Таблиця 4
67. Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу F з функцією розподілу F. Нехай Fn* - емпіричнафункція розподілу, що побудована за цією вибіркою. Тоді для будь-якого yÎ R … 67.1. … 68. Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу F з функцією розподілу F. Нехай Fn* - емпіричнафункція розподілу, що побудована за цією вибіркою. Тоді для будь-якого yÎ R … 68.1. …
69. Монету підкидають 10 разів. Знайти ймовірність з’явлення точно 5 гербів. Яке з перелічених чисел найбільш наближається до шуканої ймовірності? 69.1. 0,2 69.2. 0,25 69.3. 0,3 69.4. 0,35 70. За вибіркою Xi, i= 1, …, n з розподілу F, яка має безперервну функцію розподілу f,створена гістограма, що має k інтервалів, на яких побудовані прямокутники довжиною lj та висотою fj. Кожен з інтервалів Аj містить vj елементів вибірки. При п 70.1. ljfj 70.2. ljfj 70.3. vj /n 70.4. ljfj 71. Нижче подано доведення незміщенності оцінки для першого моменту вибірки X 1, X 2, …, Xn (Лема 1). Який з шості знаків рівності, якщо рахувати їх зліва направо, є хибним в цьому доведенні? E = E( 72. Нижче подано доведення відомої формули для дисперсії: «дисперсія рівна середньому квадрату мінус квадрат середнього». Який з чотирьох знаків рівності, якщо рахувати їх зліва направо, є хибним в цьому доведенні? 73. Укажіть, яке формулювання леми для вибіркового першого моменту є правильним? 73.1. EX = E 1 = a; X 73.2. E = EX 1 = a; 73.3. EX = E 1 = a; 73.4. E = EX1 = a; X 74. Укажіть, яке формулювання леми для вибіркової дисперсії є правильним? 74.1. E 74.2. E 74.3. E 74.4. E 75. Укажіть, яке формулювання леми для вибіркового k- го моменту є правильним? 75.1. 75.2. E 75.3. E 75.4. 76. На автоматичну телефонну станцію поступає простішій потік викликів з інтенсивністю 0,8 викл/хв. Знайти ймовірність того, що на протязі 2-х хвилин на станцію не поступить жодного виклику. До якого з перелічених чисел найбільш наближена визначена ймовірність?
76.1. 0,2 76.2. 0,4 76.3. 0,6 76.4. 0,8 77. Дана вибірка X 1, X 2, …, Xn об’єму n з параметричного сімейства розподілів Fq, qÎQ. Яка з перелічених формул не підходить для визначення оцінки параметра q* за k- ммоментом? 77.1. 77.2. 77.3. 77.4. 78. Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з функцій 78.1. 78.2. 78.3. 78.4. 79. Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з оцінок 79.1. 79.2. 79.3. 79.4. 80. Дана вибірка X 1, X 2, …, Xn об’єму n. Яка з оцінок 80.1. 80.2. 80.3. 80.4. 24. Нехай 0.950, 0.231, 0.606, 0.486, 0.891 є вибіркою об’єму 5 з рівномірного розподілу U0,θ . Знайти оцінку верхньої межі розподілу θ* за першим моментом. 24.5 0,4 24.6 0,5 24.7 0,6 24.8 0,7 25. Нехай 1.1349, -1.3312, 2.2507, 2.5754, -0.2929 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти оцінку математичного очікування a* розподілу за першим моментом. 25.1 1,0 25.2 1.5 25.3 2,0 25.4 2.5 26. Нехай 4.3818, 4.3783, 1.9247, 2.6546, 2.3493 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти зміщену оцінку дисперсії 26.1 0,01 26.2 0,02 26.3 0,03 26.4 0,04 27. Нехай 1.6266, 3.4516, 0.8234, 6.3664, 1.7272 є вибіркою об’єму 5 з нормального розподілу Na,2. Знайти незміщену оцінку дисперсії S20 розподілу за першим моментом. 27.1 0,01 27.2 0,02 27.3 0,03 27.4 0,04 28. Нехай X 1, X 2, …, Xn – вибірка об’єму п з невідомого розподілу Fq, qÎQ з функцією щільності розподілу fq. Метод максимальної правдоподібності полягає у знаходженні такого значення q*, яке відповідає екстремуму … Яким з перелічених варіантів не можна закінчити означення? 28.2 … функції 28.3 … функції 28.4 … функції 28.5 … ймовірності отримати задану вибірку X 1, X 2, …, Xn 29. Нехай 2, 1, 0, 2, 1 – вибірка об’єму 5 з розподілу Пуассона 29.5 0,1 29.6 0,2 29.7 0,3 29.8 0,4 30. Нехай 0.9355, 0.9169, 0.4103, 0.8936, 0.0579 – вибірка об’єму 5 з рівномірного розподілу U0,θ. Знайти оцінку максимальної правдоподібності верхньої межі 30.5 0,6 30.6 0,8 30.7 1,0 30.8 1,2 31. Яка з перелічених величин не може бути застосована для порівняння оцінок? (1) 31.2 | 31.3 E 31.4 E 31.5 E 32. Для одної з вибірок отримані чотири різних незміщених оцінки невідомого параметру 1,12; 1.08; 1.23; 1.11, які представляють собою випадкові величини з відповідними дисперсіями 0,28; 0.30; 0.32; 0.26. Яка з оцінок є найбільш достовірною?
32.2 1,12 32.3 1,08 32.4 1,23 32.5 1,11 33. Для кожної з чотирьох різних вибірок отримані оцінки, що мають наступні дисперсії 0,28; 0.30; 0.32; 0.26 і відповідні зміщення 0,5; 0,3; 0,3; 0,4. Знайти середній квадрат помилки для кожної з оцінок. (0,53; 0,39; 0,41; 0,42) Оцінка з яким порядковим номером є найкращою? 34. Для вибірки з рівномірного розподілу U0,θ об’ємом n обчислені середні квадрати помилок Eθ (q* - θ)2 і Eθ (
35. Нехай випадкові величини 35.1. Сума c 35.2. Сума d 35.3. Сума d 35.4. Сума c 36. Нехай X 1, X 2, …, Xn – вибірка об’єму п з розподілу Na, 36.1. 36.2. 36.3. 36.4. 37. Які з перелічених виразів відповідають означенню точного довірчого інтервалу (θ -, θ+) для параметра θ рівня довіри 1- 37.1. P(θ - < θ < θ+) 37.2. P((θ -, θ+) э θ) 37.3. P(θ - < θ < θ+) 37.4. P((θ -, θ+) э θ) 38. Який з перелічених виразів описує щільність нормального розподілу f(x) з математичним очікуванням а і середнім квадратичним відхиленням σ? 38.1. f(x) = (1/ 38.2. f(x) = (1/ 38.3. f(x) = (1/ 38.4. f(x) = (1/ 39. Нехай 0<p<1, q=1-p, m=0, 1,…, n – цілі невід’ємні числа, а С – біноміальний коефіцієнт. Дискретна випадкова величина Х має біноміальний розподіл, якщо ймовірність отримання нею значення т складає … 39.1. … Pm = Cnmpn qm 39.2. … Pm = Cmn pnqn-m 39.3. … Pm = Cnmpn-mqn 39.4. … Pm = Cnmpmqn-m 40. Випадкова величина X має розподіл Пуссона, якщоїї можливізначення 0, 1, 2, …m… складають нескінченну, але лічильну множину, а відповідні ймовірності задаються наступною формулою з параметром а, який має зміст інтенсивності потоку, … 40.1. …Pm = (am/m!) exp(-a) 40.2. …Pm = (am/m!) exp(-aт) 40.3. …Pm = (am/m!) exp(-a/m) 40.4. …Pm = (am/m!) exp(-т/а) 41. Випадкова величина X має експоненціальний розподіл, якщоїї 41.1. …f(x) = a exp(-ax) 41.2. …f(x) = a exp(-x) 41.3. …f(x) = x exp(-x) 41.4. …f(x) = x exp(-ax) 42. Яка з перелічених функцій а f(x) називається функцією Лапласа? 42.1. f(x) = 42.2. f(x) = 42.3. f(x) = 42.4. f(x) = 43. Функція розподілу для N0,1 є …
43.1. … Гама-функцією 43.2. … функцією Гевісайда 43.3. … функцією Лапласа 43.4. … одиничною функцією 44. Для визначення квантілі розподілу застосовується його … 44.1. … функція розподілу 44.2. … щільність ймовірності 44.3. … функція, обернена до функції розподілу 44.4. … функція, обернена до щільності ймовірності 45. Яка з перелічених нижче функцій щільності ймовірностей задає гама-розподіл? 45.1. 45.2. 45.3. 45.4. 46. Який з перелічених нижче виразів задає гама-функцію? 46.1. 46.2. 46.3. 46.4. 47. При λ=1 гама-розподіл 47.1. … розподіл Пуассона. 47.2. … розподіл Ерланга. 47.3.... розподіл Ст’юдента. 47.4. … експоненціальний розподіл. 48. При цілому λ>0 гама-розподіл 48.1. … розподіл Пуассона. 48.2. … розподіл Ерланга. 48.3. … розподіл Ст’юдента. 48.4. … експоненціальний розподіл. 49. Яка з наступних формул застосовна для обчислення гама-функції натурального аргументу k? 49.1. 49.2. 49.3. 49.4. 50. Якщо ξ? N0,1. то … 50.1. … ξ2 ? Γ1/2, 1/2 50.2. … ξ2 ? Γ1/2, 1 50.3. … ξ1/2 ? Γ1/2, 1/2 50.4. … ξ1/2 ? Γ1/2, 1 51. Якому з перелічених гама-розподілів належить випадкова величина, яка складає суму квадратів k незалежнихвеличин, розподілених за стандартним нормальним законом? 51.1. … Γ1/2, k 51.2. … Γ1/2, k/2 51.3. … Γ1, k 51.4. … Γ1, k/2 52. Який з перелічених розподілів називається розподілом χ2 ступеня вільності k і позначається Нk? 52.1. розподіл Γ1/2, k/2 52.2. розподіл Γ1/2, k 52.3. розподіл Г1,k/2 52.4. розподіл Г 1, k 53. Нехай ξ0, ξ1, …, ξk незалежні та мають стандартний нормальний розподіл. Розподіл якої з перелічених випадкових величин називається розподілом Ст’юдента з k ступями вільності і позначається Tk? 53.1. 53.2. 53.3. 53.4. 54. Який з розподілів для вибірки об’єму k 54.1. експоненціальний розподіл 54.2. розподіл Пуассона 54.3. розподіл Ерланга 54.4. розподіл Ст’юдента 55. Для нормального розподілу з математичним очікуванням а і дисперсією 55.1. 55.2. 55.3. 55.4. 56. Для нормального розподілу з математичним очікуванням а і дисперсією 56.1. 56.2. 56.3. 56.4. 57. Для нормального розподілу з математичним очікуванням а і дисперсією 57.1. 57.2. 57.3. 57.4. 58. Для нормального розподілу з математичним очікуванням а і дисперсією 58.1. 58.2. 58.3. 58.4. 59. Для нормального розподілу з математичним очікуванням а і дисперсією 59.1. 59.2. 59.3. 59.4. 60. Для нормального розподілу з математичним очікуванням а і дисперсією | ||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , якщо математичного очікування а =10. Визначити ширину довірчого інтервалу.
, якщо математичного очікування а =10. Визначити ширину довірчого інтервалу. . Визначити ширину довірчого інтервалу.
. Визначити ширину довірчого інтервалу. розподілу за першим моментом.
розподілу за першим моментом. . Знайти оцінку максимальної правдоподібності інтенсивності потоку
. Знайти оцінку максимальної правдоподібності інтенсивності потоку  .
. щільності розподілу.
щільності розподілу. - випадкова величина, що спостерігається у випадковому експерименті. Нехай після п -разового проведення експерименту в однакових умовах отримані значення випадкової величини X 1, X 2, …, Xn у 1-му, 2-му і т.д. експериментах. Нехай випадкова величина
- випадкова величина, що спостерігається у випадковому експерименті. Нехай після п -разового проведення експерименту в однакових умовах отримані значення випадкової величини X 1, X 2, …, Xn у 1-му, 2-му і т.д. експериментах. Нехай випадкова величина 
 E
E 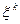 = EX 1 k = mk
= EX 1 k = mk

 )2
– зміщена дисперсія
S02 =
)2
– зміщена дисперсія
S02 =  )2
– незміщена дисперсія
)2
– незміщена дисперсія
 =
= 
 * =
* =  =
=  – Теоретичні та емпіричні моменти
– Теоретичні та емпіричні моменти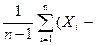 )2
– зміщена дисперсія
S02 =
)2
– зміщена дисперсія
S02 = 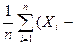 )2
– незміщена дисперсія
)2
– незміщена дисперсія
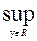 | Fn*(y)- F(y)|
| Fn*(y)- F(y)|  0 при п
0 при п 
 .
.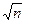
 при п
при п 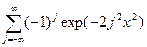 .
.
 ) =
) =  =
=  =
=  EX 1 = EX1 = a.
EX 1 = EX1 = a. =
=  - 2 E
- 2 E  +
+  =
=  - 3 E
- 3 E 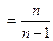 DX 1 =
DX 1 = 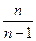
 DX 1
DX 1  = EX 1 k = mk;
= EX 1 k = mk; 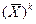

 (
( )
)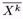 = h(
= h( )
) (
(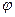 для оцінки параметра
для оцінки параметра  може бути названа статистикою?
може бути названа статистикою?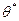 =
= 





 при п®¥
при п®¥ при п®¥
при п®¥ при п®¥
при п®¥ розподілу за першим моментом.
розподілу за першим моментом. fq (Xi)
fq (Xi)
 q* -q)2
q* -q)2 . Знайти оцінку максимальної правдоподібності інтенсивності потоку
. Знайти оцінку максимальної правдоподібності інтенсивності потоку  .
. щільності розподілу.
щільності розподілу. |
| (
(  і
і  розподілені нормально з математичними очікуваннями a1 і a2 та дисперсіями σ12 і σ22 відповідно. Нехай також g – детермінована змінна величина. Яке з перелічених тверджень є хибним у розумінні стійкості за сумуванням?
розподілені нормально з математичними очікуваннями a1 і a2 та дисперсіями σ12 і σ22 відповідно. Нехай також g – детермінована змінна величина. Яке з перелічених тверджень є хибним у розумінні стійкості за сумуванням?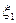 + d
+ d 



 ?
? 1-
1-  1-
1-  ) exp(-(x-a)2/(2σ2))
) exp(-(x-a)2/(2σ2)) ) exp(-(x-a)2/(2σ2))
) exp(-(x-a)2/(2σ2)) ) exp(-(x-a)2/(2σ))
) exp(-(x-a)2/(2σ))











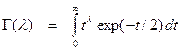
 перетворюється в …
перетворюється в …

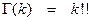




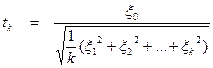
 , вибіркову дисперсію
, вибіркову дисперсію  і незміщену вибіркову дисперсію S02. Яка з перелічених випадкових величин належить до нормального стандартного розподілу?
і незміщену вибіркову дисперсію S02. Яка з перелічених випадкових величин належить до нормального стандартного розподілу?