
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похідна векторної функції за скалярним аргументомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЧАСТИНА II. КІНЕМАТИКА РОЗДІЛ 8. КІНЕМАТИКА ТОЧКИ Вступ до кінематики Кінематикою називається розділ теоретичної механіки, в якому вивчаються властивості руху тіл без врахування їх інертності (маси) і діючих на них сил. Цей розділ механіки спирається на ті основні положення геометрії, які визначають просторові співвідношення, необхідні при вивченні механічного руху. На відміну від геометрії, тут приймається до уваги ще і час руху. Таким чином, механічні рухи, що вивчаються в механіці, змінюються в просторі і часі. Нагадаємо, що в теоретичній механіці рух реальних фізичних тіл вивчається з допомогою таких абстракцій: матеріальної точки, абсолютно твердого тіла (твердого тіла), системи матеріальних точок; в розділі кінематики вони вивчаються з геометричної точки зору. Іншими словами, реальні фізичні тіла в кінематиці розглядаються як їх геометричні образи (досліджується фактично не матеріальна точка, а геометрична). Положення такого геометричного образу в просторі визначається відносно довільно вибраного другого тіла, що називається тілом відліку. Сукупність тіла відліку і зв'язаних з ним систем координатних осей та часу називається системою відліку. Системи відліку можуть бути або нерухомими, відносно деякої так званої абсолютної систем відліку (вона вважається нерухомою), або рухомими відносно останньої будь-яким чином. У множині систем відліку, в яких можна постулювати простір та час як абсолютні, виділяються так звані інерціальні системи відліку. Саме в них ізольована матеріальна точка може необмежене довго перебувати у стані спокою або рівномірного прямолінійного руху. Усі інші системи, на які не поширюються вказані властивості, називаються неінерціальними. Рух геометричного образу відносно обраної системи відліку вважається відомим, якщо можна визначити його положення в будь-який довільний момент часу. Час в механіці вважається універсальним, тобто таким, який протікає однаково у всіх системах відліку, що розглядаються. Одиниця часу - секунда. Час являється скалярною неперервною змінною величиною. В задачах кінематики час t приймають за незалежну змінну (аргумент). Всі інші змінні величини (відстані, швидкості, прискорення і т.д.) розглядають як змінні з часом, тобто як функції t. Відлік проводиться від початкового моменту (t = 0), про вибір якого в кожному випадку обумовлюється.
Рух геометричного образу відносно обраної системи відліку вважається відомим, якщо можна визначити його положення у будь-який довільний момент часу. Положення геометричного образу відносно даної системи відліку визначається відповідними параметрами, а його рух - рівняннями, що виражають ці параметри як функції часу. Встановлення способів, за допомогою яких можна задати рух геометричного образу відносно вибраної системи відліку, є однією із задач кінематики. Основна задача кінематики полягає в тому, щоб за кінематичними залежностями руху даного геометричного образу визначити всі кінематичні характеристики цього руху (траєкторії точок, їхні лінійні швидкості та прискорення; кутові швидкість та прискорення тіла). Неперервну криву, яку описує точка в своєму русі, називають траєкторією точки. Якщо траєкторія є прямою лінією, то рух називається прямолінійним, а якщо кривою - криволінійним. При русі тіла всі його точки, в загальному випадку, здійснюють різні рухи. Тому вивченню руху тіла повинно передувати вивчення руху точки.
Способи опису руху точки
Рівняння, що дозволяють визначити положення точки у вибраній системі відліку в будь-який момент часу, називається кінематичними залежностями руху точки. Ці рівняння мають різний вигляд, залежно від способу визначення руху точки. Для опису криволінійного руху точки можна застосувати один з трьох способів: векторний, координатний та натуральний. При векторному способі опису руху положення точки у вибраній системі відліку в довільний момент часу визначається радіус-вектором, відносно деякої фіксованої точки О - полюса (рис. 8.1), тобто,
 (8.1) (8.1)
Якщо будувати функцію
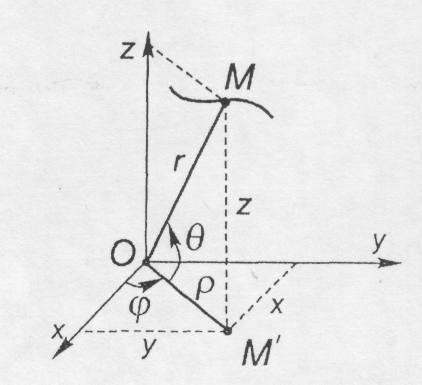
При координатному способі опису руху положення точки М в довільний момент часу визначається її координатами у вибраній системі координат (декартовій, циліндричній, сферичній тощо), незмінно пов'язаній з тілом відліку. У прямокутній декартовій системі координат положення точки М визначається координатами x,y,z (рис. 8.3) як функціями часу.
Співвідношення (8.2) називаються кінематичними рівняннями руху точки у координатній декартовій формі, їх можна розглядати як рівняння траєкторії точки у параметричній формі (параметром є час t). Зв'язок між векторним та координатним декартовим способами опису руху точки задається співвідношенням:
Рис. 8.3 Рис. 8.4
де У сферичній системі координат, положення точки визначається полярним радіусом r, полярним кутом φ між віссю Ох і напрямом ОМ’ (М’ - проекція точки М на площину Оху, кутом θ між ОМ' і ОМ (рис. 8.4). В процесі руху точки величини r,φ,θзмінюються - вони є функціями часу:
Співвідношення (8.4) називають кінематичними рівняннями руху точки у координатній сферичній формі. Зв'язок між координатним декартовим і координатним сферичним способами опису руху точки задається співвідношеннями:
У циліндричній системі координат (рис. 8.4) положення точки визначається радіусом р, кутом φ між віссю Ох та ОМ' (азимутом), координатою z = MM'. В процесі руху ці величини змінюються як функції часу:
Співвідношення (8.6) називають кінематичними рівняннями руху точки у координатній циліндричній формі. Зв'язок між координатним декартовим і координатним циліндричним способами опису руху точки такий:
функціями часу:
Співвідношення (8.8) називається кінематичними рівняннями руху точки у координатній полярній формі.
Рівняння руху точки (8.2) є одночасно і рівняннями траєкторії точки в параметричній формі, де роль параметра відіграє час t. Для того, щоб одержати рівняння траєкторії у координатній формі, необхідно з рівнянь руху виключити час t. Нехай, наприклад, рух точки в площині ху описаний рівняннями:
де а,b,с - постійні величини.
де а,b,ω - постійні величини.
Зведемо до квадрата ліву і праву частини рівнянь і складемо:
Рис. 8.7 Рис. 8.8 Це рівняння еліпса з напівосями а і b (рис. 8.7). Натуральний спосіб опису руху точки застосовується тоді, коли траєкторія точки заздалегідь відома. Положення точки у вибраній системі відліку визначають такі елементи (рис. 8.8): а) просторова крива АВ (траєкторія точки). б) початок відліку О дугової координати σ. в) додатний напрям відліку дугової координати; г) дугова координата σ на кривій. В процесі руху точки М дугова координата σ змінюється за часом:
Співвідношення (8.10) називається кінематичним рівнянням руху точки у натуральній формі. Не можна змішувати кінематичні рівняння з рівнянням траєкторії. Крива, побудована на площині (σ, t) та виражає залежність
Встановимо зв'язок між координатами, декартовим і натуральним способами опису руху точки. Нехай рух точки описаний рівняннями (8.2). Виключаючи з цих рівнянь час t. одержимо рівняння траєкторії. Знайдемо тепер закон руху З курсу диференціальної геометрії відомо, що елемент дуги траєкторії d σвизначається виразом:
де dx,dy,dz - диференціали координат точки.
тоді формулу (1.12) можна записати у вигляді:
Інтегруючи цей вираз в інтервалі від t = О (початок руху) до будь-якого моменту t, одержимо закон руху:
Знак „+" перед інтегралом слід вибирати в тому випадку, коли рух проходить в бік додатного відліку дугової координати, та „-" при русі точки в бік від'ємного відліку дугової координати.
Рис. 8.9 На годографі (рис. 8.9) вектор Вектор
Отже, похідна вектора за скалярним аргументом являє собою вектор, проекції якого на нерухомі осі дорівнюють похідним за тим самим аргументом від проекцій диференційованого вектора.
Модуль похідної визначається з рівності
Подамо без доведення властивості похідної вектора за скалярним аргументом: 1. Похідна від постійного за величиною і напрямом вектора дорівнює нулю. 2. Похідна від суми векторів дорівнює сумі похідних, тобто,
3. Похідні від скалярного і векторного добутків векторів відповідно визначаються виразами:
Перейдемо тепер до визначення поняття швидкості руху точки і методу її знаходження.
Швидкість точки Рис. 8.10
Рис. 8.11
Розглянемо вектори швидкостей Рис. 8.14
Оскільки границя відношення дуги до стягуючої її хорди дорівнює за модулем одиниці, а граничне положення січної ММ1 співпадає з напрямком до дотичної до кривої в точці М, то
де Направлений одиничний вектор дотичної Приймаючи до уваги, що
Проектуючи вектор швидкості
Очевидно, що v𝜏 = v, якщо рух точки проходить в бік додатного відліку дуги і v𝜏 = -v, якщо рух точки проходить в протилежну сторону, отже Так як шлях, що проходить точка, завжди додатний, то елемент шляху і, отже, модуль швидкості можна визначити за формулою:
Прискорення точки Рис. 8.15
Рис. 8.16
Беручи до уваги формули (8.26) та (8.27), отримаємо:
Цей вираз являє собою розклад вектора прискорення точки на радіальний і трансверсальний напрями (рис. 8.16). Відповідні складові прискорення позначимо через Тоді,
Де Модуль та напрям вектора прискорення точки у полярних координатах визначаються за формулами:
Рис. 8.17 Розглянемо просторову криву. Нехай
Рис. 8.18
Візьмемо на кривій точку М1, близьку до точки М і проведемо одиничний вектор дотичний цій точці
Таким чином, у кожній площині кривої можна вказати три взаємно перпендикулярні напрямки, за якими можна провести дотичну у бік зростання дугової координати (орт Зауважимо, що плоска крива повністю лежить у стичній площині, а головна нормаль буде нормаллю до кривої у цій площині. Введемо поняття кривизни кривої. Позначимо через Цей кут називається кутом суміжності. Кривиною кривої в точці М називають границю відношення кута суміжності до абсолютного значення дуги ММ1 = ∆σ.
Величину, обернену кривині в точці М, називають радіусом кривини:
Зауважимо, що кривина прямої дорівнює нулю, а радіус дорівнює безкінечності. Кривина кола в усіх його точках однакова і дорівнює оберненій величині радіуса Рис. 8.19, а
Рис. 8.19, б
Вектор Отже, вектор Таким чином, вектор Знайдемо тепер величину
Враховуючи, що
З цієї формули випливає, що вектор прискорення лежить в стичній площині. Складові прискорення за напрямами
Проекція прискорення на напрямок
називається дотичним прискоренням. Проекція прискорення на головну нормаль
називається нормальним прискоренням. Нормальне прискорення Дотичне прискорення характеризує зміну швидкості за величиною, а нормальне прискорення - зміну швидкості за напрямком. Модуль вектора прискорення.
Дотичне прискорення Якщо Якщо ж
а) Рис 8.20 б) При Нормальне прискорення дорівнює нулю при прямолінійному русі ( Радіус кривини траєкторії можна визначити за формулою:
Зазначимо, що для обчислення дотичного прискорення Якщо рух точки задано координатним способом, у випадку опису руху в декартових координатах
Для полярних координат одержимо:
Рівнозмінний рух точки
Якщо Встановимо закон зміни швидкості і закон руху точки по траєкторії при рівнозмінному русі. Оскільки.
Сталу інтегрування С1, знайдемо, виходячи з початкових умов. Нехай, наприклад, при t = О,
Так як Звідки, інтегруючи, одержимо:
Нехай, наприклад, при t = 0
Прямолінійний рух точки
Якщо траєкторія точки є прямою лінією, то направляючи одну з координат осей, наприклад, вісь х, вздовж цієї прямої, ми повністю визначимо положення точки заданням її абсциси як функції часу, тобто х = x(t). Проекції швидкості і прискорення точки на вісь х згідно формул (8.20) і (8.33) будуть
Модулі швидкості і прискорення відповідно рівні:
Якщо
де α,ω,ε - постійні величини. Рух точки за таким законом називають гармонійним. Величина α, що дорівнює максимальному відхиленню точки від положення х = 0, називається амплітудою коливань; Швидкість і прискорення точки, що здійснює гармонійне коливання, відповідно будуть
З формули для Рух за гармонійним законом буде періодичним рухом, тобто через рівні проміжки часу буде повністю повторюватись. Найменший проміжок часу, після закінчення якого рух повторюється, називається періодом коливань. Якщо позначити через Т період коливань, то буде справедлива рівність:
звідки
Кількість коливань за одиницю часу називається частотою коливань і дорівнює Питання для самоконтролю
1. Що означає рух точки? 2. Як визначається рівняння траєкторії при координатному способі опису руху? 3. Яка існує залежність між елементом дугової координати і елементом шляху? 4. Чи можна, знаючи закон руху точки по траєкторії, визначити траєкторією? 5. Коли перед інтегралом для визначення дугової координати необхідно брати "+" і коли "-"? 6. Що називається годографом вектора? 7. Як направлена похідна вектора за скалярним аргументом? 8. Яка існує залежність між радіусом-вектором точки, що рухається. і вектором швидкості цієї точки? 9. Чому дорівнюють проекції швидкостей на декартові осі координат? 10. Рух точки описаний полярними координатами. Як виражаються проекції швидкості на радіальний і поперечний напрямок? 11. Як виражається модуль вектора швидкості точки при натуральному способі опису руху? 12. Яка існує залежність між радіусом-вектором і прискоренням точки? 13. Чому дорівнюють проекції прискорення на осі декартової системи координат? 14. Які осі називаються натуральними? Що таке стична площина? 15. Чому дорівнюють проекції прискорення на дотичну, головну нормаль і бінормаль? 16. Який напрямок має вектор 17. Яку зміну швидкості характеризують нормальне і дотичне прискорення? 18. Як визначається кінематичний радіус кривини?
Задача 8.1 Рух точки задано рівняннями:
де a і b - постійні додатні числа (x, у в см, t в с). Визначити траєкторію руху точки і закон руху точки по траєкторії, вважаючи відстань від початкового положення точки. Розв'язання 1) Визначення траєкторії руху точки. Для одержання рівняння траєкторії в координатній формі необхідно з її параметричних рівнянь виключити параметр t. Оскільки Це рівняння прямої лінії у відрізках на осях (рис. 8.21).
Рис. 8.21 З рівнянь руху точки виходить, що
тобто траєкторією точки є не вся пряма, а її відрізок M0M1. Точка здійснює коливальний рух на цьому відрізку. В моменти 2) Визначення закону руху по траєкторії. Закон pуxy по траєкторії визначається формулою:
При русі від М0 до М1 рухома координата σзростає і перед законом інтегрування необхідно поставити знак "+". Оскільки при цьому sin 2t > О, то "+" під знаком інтегрування можна відкинути. При русі точки від М 1 до М0 рухома координата зменшується і перед знаком інтеграла слід поставити знак "-". При цьому sin 2t < О, то можна відкинути одночасно знак мінус перед інтегралом і знак "-" під інтегралом. Таким чином, для будь-якого моменту часу t маємо
Задача 8.2 Визначити траєкторію точки М середини шатуна кривошипно-шатунного механізму (рис. 8.22), якщо ОА = АВ = а см, а кут
Рис. 8.22
1) Визначення траєкторії точки. Для визначення траєкторії точки М знайдемо спочатку рівняння її руху, тобто визначимо координати точки М через параметр t. Положення механізму слід показати в поточний момент часу. Згідно рис. 8.22 маємо
Для визначення траєкторії точки М необхідно з рівнянь руху (СІ) виключити параметр t:
Піднісши рівняння (б) до квадрата і додаючи їх, одержимо:
Траєкторією точки М є еліпс з на півосями 2) Визначення швидкості повзуна: В. Рівняння руху повзуна
Проекція швидкості повзуна на вісь Ох
а величина швидкості
Проекція і величина швидкості повзуна в момент
Так як проекція швидкості повзуна на вісь від'ємна величина, то вектор швидкості повзуна при 3) Визначення швидкості точки М. Проекції швидкості точки М на осі координат
а величина швидкості
4) Визначення прискорення повзуна В. Проекція прискорення повзуна на вісь
а величина прискорення
Величина прискорення повзуна і його проекція на вісь Ох при 5) Визначення прискорення точки М. Проекції прискорення точки М на осі координат
а величина прискорення точки М
|

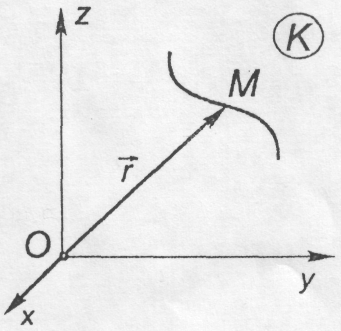
 в різні моменти часу t1, t2,..., tn, то геометричним місцем кінців М1, М2,..., Мі,..., Мn, буде крива, яка називається траєкторією рухомої точки (рис. 8.2). Отже, співвідношення (1.1) можна розглядати як рівняння траєкторії точки. Задати вектор, як функцію часу - це означає вміти находити його величину і напрям в будь-який момент часу. Це можна зробити, якщо вибрана будь-яка система координат. Тобто, завдання радіуса-вектора як функції часу, обов'язково передбачає наявність системи координат, але в той самий час не зв'язує нас із конкретною системою координат. Ця обставина дозволяє широко використовувати завдання радіуса-вектора як функції часу для одержання основних кінематичних характеристик руху.
в різні моменти часу t1, t2,..., tn, то геометричним місцем кінців М1, М2,..., Мі,..., Мn, буде крива, яка називається траєкторією рухомої точки (рис. 8.2). Отже, співвідношення (1.1) можна розглядати як рівняння траєкторії точки. Задати вектор, як функцію часу - це означає вміти находити його величину і напрям в будь-який момент часу. Це можна зробити, якщо вибрана будь-яка система координат. Тобто, завдання радіуса-вектора як функції часу, обов'язково передбачає наявність системи координат, але в той самий час не зв'язує нас із конкретною системою координат. Ця обставина дозволяє широко використовувати завдання радіуса-вектора як функції часу для одержання основних кінематичних характеристик руху. Для розв'язування конкретних задач, зазвичай, переходять від векторного способу до координатного або натурального способів завдання руху.
Для розв'язування конкретних задач, зазвичай, переходять від векторного способу до координатного або натурального способів завдання руху. (8.2)
(8.2)
 (8.3)
(8.3)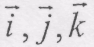 - орти (одиничні вектори) системи координат Oxyz (рис. 8.3).
- орти (одиничні вектори) системи координат Oxyz (рис. 8.3). (8.4)
(8.4) (8.5)
(8.5) (8.6)
(8.6) (8.7)
(8.7)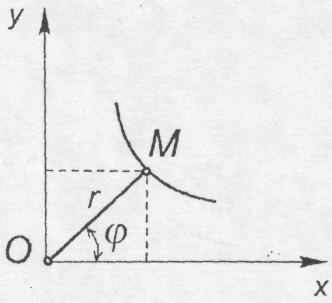 При дослідженні руху точки на площині використовується також полярна система координат (рис. 8.5). Полярними координатами точки є радіус r і кут φ є процесі руху точки вони є
При дослідженні руху точки на площині використовується також полярна система координат (рис. 8.5). Полярними координатами точки є радіус r і кут φ є процесі руху точки вони є (8.8)
(8.8) (8.9)
(8.9)
 З першого рівняння визначаємо
З першого рівняння визначаємо  і підставляємо його в друге рівняння
і підставляємо його в друге рівняння  . Це рівняння параболи. Однак траєкторією буде не вся парабола, а тільки її права гілка (при t = 0; х = 0; у = с), оскільки час додатний і безперервно зростає (рис. 8.6). Такий метод виключення часу не єдиний. Існують й інші способи. Наприклад, рух точки описаний рівняннями:
. Це рівняння параболи. Однак траєкторією буде не вся парабола, а тільки її права гілка (при t = 0; х = 0; у = с), оскільки час додатний і безперервно зростає (рис. 8.6). Такий метод виключення часу не єдиний. Існують й інші способи. Наприклад, рух точки описаний рівняннями:
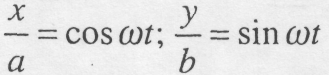


 (8.10)
(8.10) називається графіком руху. Якщо рух точки проходить в сторону зростання дуги σ, то диференціал дуги
називається графіком руху. Якщо рух точки проходить в сторону зростання дуги σ, то диференціал дуги  буде додатним, якщо рух проходить в бік зменшення дуги, то d σбуде від'ємним. Відзначимо, що шлях S, який проходить точка, весь час буде зростати і, отже, додатний, тобто,
буде додатним, якщо рух проходить в бік зменшення дуги, то d σбуде від'ємним. Відзначимо, що шлях S, який проходить точка, весь час буде зростати і, отже, додатний, тобто,
 .
. (8.11)
(8.11)
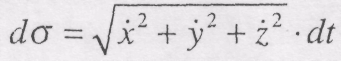 (8.11а)
(8.11а) (8.12)
(8.12)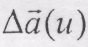 спрямований по хорді, тобто по січній MM1, граничне положення якої при ∆u → 0 (точка прямує до точки М) збігається з дотичною
спрямований по хорді, тобто по січній MM1, граничне положення якої при ∆u → 0 (точка прямує до точки М) збігається з дотичною  до годографа вектора
до годографа вектора  у точці М.
у точці М. характеризує швидкість зміни вектора
характеризує швидкість зміни вектора  при зміні його аргументу і спрямований по дотичній до годографа, яка проведена у бік зростання значення скалярного аргументу. Якщо вектор
при зміні його аргументу і спрямований по дотичній до годографа, яка проведена у бік зростання значення скалярного аргументу. Якщо вектор  виразити через його проекції аx,аy, аz, на нерухомі осі Ox,Oy,Oz, тобто
виразити через його проекції аx,аy, аz, на нерухомі осі Ox,Oy,Oz, тобто  , то враховуючи, що орти
, то враховуючи, що орти  є сталими величинами, дістаємо
є сталими величинами, дістаємо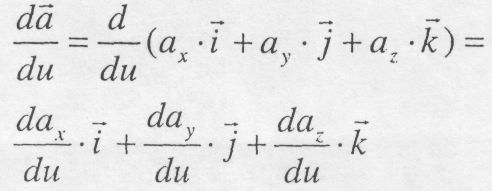 (8.14)
(8.14) (8.5)
(8.5)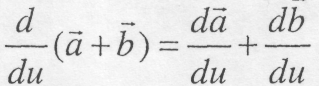 (8.16)
(8.16) (8.17)
(8.17)
 (рис. 8.11, а) руху точки М по траєкторії. Виберемо довільну нерухому точку О’ (рис. 8.11) та перенесемо всі вектори швидкості паралельно так, щоб їхні початки збігалися з точкою О’. Оскільки вектор
(рис. 8.11, а) руху точки М по траєкторії. Виберемо довільну нерухому точку О’ (рис. 8.11) та перенесемо всі вектори швидкості паралельно так, щоб їхні початки збігалися з точкою О’. Оскільки вектор 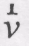 змінюється за часом, то кінці перенесених векторів
змінюється за часом, то кінці перенесених векторів  утворюють неперервну криву, яка називається годографом вектора швидкості.
утворюють неперервну криву, яка називається годографом вектора швидкості.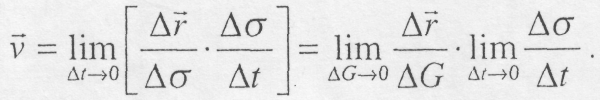

 - одиничний вектор, направлений по дотичній до кривої.
- одиничний вектор, направлений по дотичній до кривої. завжди в сторону додатного відліку дуги σ. Дійсно, якщо
завжди в сторону додатного відліку дуги σ. Дійсно, якщо  то вектор
то вектор  направлений в сторону
направлений в сторону  (рис. 8.14.а), а при
(рис. 8.14.а), а при 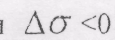 вектор направлений в сторону, протилежну
вектор направлений в сторону, протилежну  (рис. 8.14,6). В обох випадках цей вектор, а отже і його границя
(рис. 8.14,6). В обох випадках цей вектор, а отже і його границя 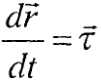 , направлений в сторону зростання дуги σ.
, направлений в сторону зростання дуги σ.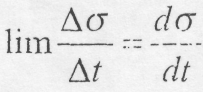 маємо
маємо
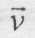 на напрям
на напрям  , одержимо
, одержимо , отже
, отже (8.29)
(8.29)
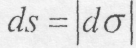

 (8.36)
(8.36) (8.37)
(8.37) і
і  .
. (8.38)
(8.38) (8.39)
(8.39) (8.40)
(8.40) (8.41)
(8.41) буде одиничним вектором дотичної, проведеної в деякій точці М кривої (рис. 8.17).
буде одиничним вектором дотичної, проведеної в деякій точці М кривої (рис. 8.17).
 . Перенесемо вектор
. Перенесемо вектор  в точку М і проведемо площину через вектори
в точку М і проведемо площину через вектори  і
і  , прикладені в точці М. При наближенні точки М1 до точки М ця площина буде повертатись навколо
, прикладені в точці М. При наближенні точки М1 до точки М ця площина буде повертатись навколо  і в границі займе певне положення. Одержану таким чином площину називають стичною. Через точку М проведемо площину, перпендикулярну до дотичної
і в границі займе певне положення. Одержану таким чином площину називають стичною. Через точку М проведемо площину, перпендикулярну до дотичної  ; вона називається нормальною площиною (рис. 8.18). Очевидно, що будь-яка пряма у цій площині, яка проходить через точку М, буде перпендикулярна до
; вона називається нормальною площиною (рис. 8.18). Очевидно, що будь-яка пряма у цій площині, яка проходить через точку М, буде перпендикулярна до  тобто буде нормаллю до кривої. Отже, головна нормаль - це одна з нескінченної множини нормалей до кривої в точці М, яка лежить в стичній площині. Площина, що проходить через точку М перпендикулярно до головної нормалі, називається спрямною. Лінія перетину спрямляючої та нормальної площин визначає бінормаль кривої. Очевидно, що бінормаль перпендикулярна до головної нормалі.
тобто буде нормаллю до кривої. Отже, головна нормаль - це одна з нескінченної множини нормалей до кривої в точці М, яка лежить в стичній площині. Площина, що проходить через точку М перпендикулярно до головної нормалі, називається спрямною. Лінія перетину спрямляючої та нормальної площин визначає бінормаль кривої. Очевидно, що бінормаль перпендикулярна до головної нормалі. ), головну нормаль в бік ввігнутості кривої (відповідний орт
), головну нормаль в бік ввігнутості кривої (відповідний орт  ), бінормаль з відповідним ортом
), бінормаль з відповідним ортом  спрямовану так, що орти
спрямовану так, що орти  ,
,  та
та  утворюють праву ортогональну трійку векторів. Прямокутна система координатних осей за ортами
утворюють праву ортогональну трійку векторів. Прямокутна система координатних осей за ортами  ,
,  ,
,  з початком в точці М утворюють праву ортогональну трійку векторів. Прямокутна система координатних осей за ортами
з початком в точці М утворюють праву ортогональну трійку векторів. Прямокутна система координатних осей за ортами  ,
,  ,
,  величину кута між векторами
величину кута між векторами  і
і  , проведену в точці М (рис. 8.17).
, проведену в точці М (рис. 8.17). (8.42)
(8.42) (8.43)
(8.43) ; радіус кривини дорівнює радіусу кола
; радіус кривини дорівнює радіусу кола  .
.
 буде завжди направлений в бік ввігнутості траєкторії (рис. 1.19, а і б), тому що при
буде завжди направлений в бік ввігнутості траєкторії (рис. 1.19, а і б), тому що при 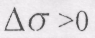 вектор
вектор  направлений протилежно вектору
направлений протилежно вектору  , при
, при  він направлений в той самий бік, що і вектор
він направлений в той самий бік, що і вектор  . Вектор
. Вектор  і
і  (площина МАВ).
(площина МАВ). лежить в стичній площині, оскільки при
лежить в стичній площині, оскільки при  площина МАВ збігається з стичною площиною в точці М.
площина МАВ збігається з стичною площиною в точці М. лежить в стичній площині, направлений в бік ввігнутості траєкторії, перпендикулярний до
лежить в стичній площині, направлений в бік ввігнутості траєкторії, перпендикулярний до  , отже, він направлений по головній нормалі до центра кривини.
, отже, він направлений по головній нормалі до центра кривини. . Трикутник АМВ рівнобічний (рис. 8.19,а), отже,
. Трикутник АМВ рівнобічний (рис. 8.19,а), отже, або користуючись рівняннями (8.43) і (1.44). одержимо:
або користуючись рівняннями (8.43) і (1.44). одержимо:
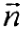 одиничний вектор головної нормалі, будемо мати:
одиничний вектор головної нормалі, будемо мати: і, отже
і, отже (8.47)
(8.47) і
і 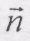 відповідно будуть:
відповідно будуть: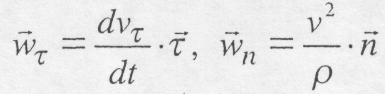

 (8.48)
(8.48)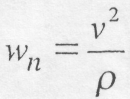 (8.49)
(8.49) . Проекція прискорення на бінормаль дорівнює нулю.
. Проекція прискорення на бінормаль дорівнює нулю.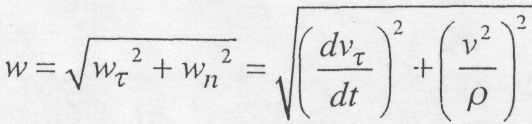 (8.50)
(8.50) дорівнює нулю при русі точки з постійною за модулем швидкістю і в момент часу, в якій швидкість
дорівнює нулю при русі точки з постійною за модулем швидкістю і в момент часу, в якій швидкість 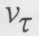 досягає екстремальних значень.
досягає екстремальних значень.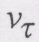 і
і  одного знака, то модуль швидкості
одного знака, то модуль швидкості  точки зростає і рух в цьому випадку називається прискореним (рис. 8.20а).
точки зростає і рух в цьому випадку називається прискореним (рис. 8.20а). спадає і рух буде сповільненим (рис. 8.20 б).
спадає і рух буде сповільненим (рис. 8.20 б).

 модуль швидкості залишається постійним і рух буде рівномірним.
модуль швидкості залишається постійним і рух буде рівномірним. J, а також в точках перегину криволінійної траєкторії і в моменти часу, при якому швидкість точки дорівнює нулю.
J, а також в точках перегину криволінійної траєкторії і в моменти часу, при якому швидкість точки дорівнює нулю. (8.51)
(8.51)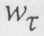 можна використати рівність
можна використати рівність  , оскільки
, оскільки 
 то будемо мати:
то будемо мати: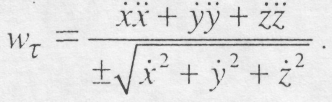

 - постійна величина, то рух точки називається рівнозмінним.
- постійна величина, то рух точки називається рівнозмінним. , то
, то  і
і 
 , тоді
, тоді  . Закон зміни швидкості прийме вигляд:
. Закон зміни швидкості прийме вигляд: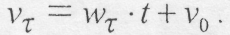 (8.52)
(8.52)

 , тоді
, тоді  і закон руху точки по заданій траєкторії буде мати вигляд:
і закон руху точки по заданій траєкторії буде мати вигляд: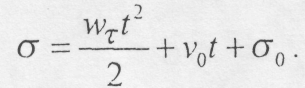 (8.53)
(8.53)

 , точки проходить в бік додатнього напрямку осі x. Якщо при цьому
, точки проходить в бік додатнього напрямку осі x. Якщо при цьому  , то рух буде прискорений, якщо ж
, то рух буде прискорений, якщо ж  то рух сповільнений. При
то рух сповільнений. При  точка рухається в напрямку протилежному додатному напрямку осі x. Якщо при цьому
точка рухається в напрямку протилежному додатному напрямку осі x. Якщо при цьому  , то рух сповільнений, якщо ж
, то рух сповільнений, якщо ж 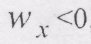 , то рух прискорений. Як приклад, розглянемо прямолінійний рух точки. За законом
, то рух прискорений. Як приклад, розглянемо прямолінійний рух точки. За законом ,
,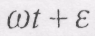 називається фазою і ε - початковою фазою коливань.
називається фазою і ε - початковою фазою коливань.
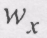 випливає, що прискорення точки завжди направлено до початку координат і за модулем пропорційне відхиленню точки від початку координат.
випливає, що прискорення точки завжди направлено до початку координат і за модулем пропорційне відхиленню точки від початку координат. ,
,
 . Якщо час вимірюється в секундах, то частота вимірюється в герцах. Кругова частота дорівнює кількості коливань за
. Якщо час вимірюється в секундах, то частота вимірюється в герцах. Кругова частота дорівнює кількості коливань за  одиниць часу.
одиниць часу. ?
?
 , то
, то 


 точка перебуває в точці M0, в моментів
точка перебуває в точці M0, в моментів 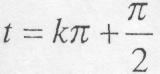 точці M1 (k = 0,1,2...)
точці M1 (k = 0,1,2...)



 радіан. Визначити також швидкість і прискорення точки М і повзуна В в момент
радіан. Визначити також швидкість і прискорення точки М і повзуна В в момент 


 (a)
(a) (б)
(б)

 і
і  . В початковий момент координати точки М дорівнюють
. В початковий момент координати точки М дорівнюють  і 0.
і 0.

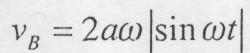
 будуть:
будуть:
 направлений в протилежний бік осі Ох.
направлений в протилежний бік осі Ох.




 від'ємна величина, то
від'ємна величина, то  направлено в протилежну сторону Ох, тобто від В до О.
направлено в протилежну сторону Ох, тобто від В до О.



