
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методичні вказівки до розв'язання задачСодержание книги Поиск на нашем сайте
При розв'язанні задач на складання рівнянь руху точки необхідно виразити координати точки, що рухається, відносно вибраної системи координат через час. При цьому положення точки необхідно показати в поточний момент часу. Якщо рівняння руху точки відомі, то для одержання кривої, по якій рухається точка, необхідно з рівнянь її руху виключити час. Якщо рух точки описано в декартовій системі координат, а необхідно перейти до натурального способу опису руху точки, то траєкторію точки визначають за вищевказаним правилом, вибирають на ній початок і направлення відліку дугової координати, а закон руху точки по визначеній траєкторії визначають за формулою:
Знак "+" вибирають в тому випадку, коли точка рухається в бік зростання дугової координати, а “-“ коли точка рухається в зворотному напрямку. Визначення швидкості, дотичного, нормального і повного прискорення, а також радіуса кривизни кривої проводиться за відповідними формулами кінематики точки. Для того, щоб правильно показати на рисунку вектори швидкості, дотичного, нормального і повного прискорень точки, слід враховувати знаки проекцій цих векторів на відповідні координатні осі.
Задача 8.1 Рух точки задано рівняннями:
де a і b - постійні додатні числа (x, у в см, t в с). Визначити траєкторію руху точки і закон руху точки по траєкторії, вважаючи відстань від початкового положення точки. Розв'язання 1) Визначення траєкторії руху точки. Для одержання рівняння траєкторії в координатній формі необхідно з її параметричних рівнянь виключити параметр t. Оскільки Це рівняння прямої лінії у відрізках на осях (рис. 8.21).
Рис. 8.21 З рівнянь руху точки виходить, що
тобто траєкторією точки є не вся пряма, а її відрізок M0M1. Точка здійснює коливальний рух на цьому відрізку. В моменти 2) Визначення закону руху по траєкторії. Закон pуxy по траєкторії визначається формулою:
При русі від М0 до М1 рухома координата σзростає і перед законом інтегрування необхідно поставити знак "+". Оскільки при цьому sin 2t > О, то "+" під знаком інтегрування можна відкинути. При русі точки від М 1 до М0 рухома координата зменшується і перед знаком інтеграла слід поставити знак "-". При цьому sin 2t < О, то можна відкинути одночасно знак мінус перед інтегралом і знак "-" під інтегралом. Таким чином, для будь-якого моменту часу t маємо
Задача 8.2 Визначити траєкторію точки М середини шатуна кривошипно-шатунного механізму (рис. 8.22), якщо ОА = АВ = а см, а кут
Рис. 8.22
1) Визначення траєкторії точки. Для визначення траєкторії точки М знайдемо спочатку рівняння її руху, тобто визначимо координати точки М через параметр t. Положення механізму слід показати в поточний момент часу. Згідно рис. 8.22 маємо
Для визначення траєкторії точки М необхідно з рівнянь руху (СІ) виключити параметр t:
Піднісши рівняння (б) до квадрата і додаючи їх, одержимо:
Траєкторією точки М є еліпс з на півосями 2) Визначення швидкості повзуна: В. Рівняння руху повзуна
Проекція швидкості повзуна на вісь Ох
а величина швидкості
Проекція і величина швидкості повзуна в момент
Так як проекція швидкості повзуна на вісь від'ємна величина, то вектор швидкості повзуна при 3) Визначення швидкості точки М. Проекції швидкості точки М на осі координат
а величина швидкості
4) Визначення прискорення повзуна В. Проекція прискорення повзуна на вісь
а величина прискорення
Величина прискорення повзуна і його проекція на вісь Ох при 5) Визначення прискорення точки М. Проекції прискорення точки М на осі координат
а величина прискорення точки М
оскільки то
Напрямні косинуси вектора
Напрямляючі конуси вектора WМ мають протилежні знаки з напрямляючими косинусами вектора
Задача 8.3 Рух точки заданий рівняннями
де а, b, c — постійні додатні числа (x, у в м, t в с). Визначити рівняння траєкторії, а також швидкість, дотичне, нормальне і повне прискорення точки, радіус кривини в довільний і початковий моменти часу. Визначити висоту траєкторії і дальність польоту точки. Вісь Ох направлена горизонтально, вісь Оу - вертикально вгору. Розв'язання 1) Визначення траєкторії точки. З рівнянь руху виключаємо параметр t. Для цього з першого рівняння знаходимо
Траєкторією точки є парабола (рис. 8.23).
Рис. 8.23 2) Визначення швидкості точки. Проекції швидкості на осі координат
Величина швидкості точки
а в момент t = О
2) Визначення дотичного прискорення. Так як рух точки проходить в бік зростання, то вектори
а в початковий момент
В початковий момент вектор дотичного прискорення направлений в протилежну сторону швидкості, оскільки при t = 0 велична 4) Визначення повного прискорення точки. Проекції прискорення на осі координат:
а повне прискорення 5) Визначення нормального прискорення точки. Нормальне прискорення точки в момент t
а в початковий момент Нормальне прискорення завжди направлене по головній нормалі в бік ввігнутості кривої. б) Визначення радіуса кривини.
а в початковий момент 7) Визначення висоти траєкторії. В момент t1, коли точка досягне найвищого положення
Підставивши значення t1 в вираз для у, одержимо 8) Визначення дальності польоту точки. В момент зустрічі точки з Землею
Звідки одержуємо t1=0 (початкове положення точки) і
На рис. 8.23 показані швидкості і прискорення точки в різних місцях траєкторії.
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.56.125 (0.011 с.) |



 , то
, то 


 точка перебуває в точці M0, в моментів
точка перебуває в точці M0, в моментів 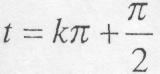 точці M1 (k = 0,1,2...)
точці M1 (k = 0,1,2...)



 радіан. Визначити також швидкість і прискорення точки М і повзуна В в момент
радіан. Визначити також швидкість і прискорення точки М і повзуна В в момент 


 (a)
(a) (б)
(б)

 і
і  . В початковий момент координати точки М дорівнюють
. В початковий момент координати точки М дорівнюють  і 0.
і 0.

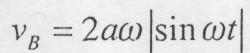
 будуть:
будуть:
 направлений в протилежний бік осі Ох.
направлений в протилежний бік осі Ох.




 від'ємна величина, то
від'ємна величина, то  направлено в протилежну сторону Ох, тобто від В до О.
направлено в протилежну сторону Ох, тобто від В до О.





 , тому вектор
, тому вектор  має направлення, протилежне вектору
має направлення, протилежне вектору 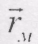 , тобто він направлений від М до О.
, тобто він направлений від М до О.
 ,
,



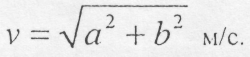
 направлені в одну сторону і, отже, маємо
направлені в одну сторону і, отже, маємо 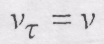 Тому
Тому

 від'ємна (рис.8.23).
від'ємна (рис.8.23).
 . Повне прискорення залежить від часу. Вектор направлений в протилежний бік додатного напрямку осі Оу, так як
. Повне прискорення залежить від часу. Вектор направлений в протилежний бік додатного напрямку осі Оу, так як  , а
, а  - від'ємна величина.
- від'ємна величина.



 , звідки
, звідки  .
.
 c, а дальність польоту точки
c, а дальність польоту точки м.
м.


