
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розкладання вектора прискорення точки за осями натурального тригранника (нормальна і дотична складові прискорення)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вектор швидкості може бути представленим у вигляді
де На основі виразу (8.32) маємо:
Подамо похідну
Підставивши (8.45) в (8.44), одержимо:
оскільки Визначимо величину і напрямок вектора Нехай в момент часу t точка перебуває в положенні М на траєкторії, а в момент Вектор
Рис. 8.19, а
Рис. 8.19, б
Вектор Отже, вектор Таким чином, вектор Знайдемо тепер величину
Враховуючи, що
З цієї формули випливає, що вектор прискорення лежить в стичній площині. Складові прискорення за напрямами
Проекція прискорення на напрямок
називається дотичним прискоренням. Проекція прискорення на головну нормаль
називається нормальним прискоренням. Нормальне прискорення Дотичне прискорення характеризує зміну швидкості за величиною, а нормальне прискорення - зміну швидкості за напрямком. Модуль вектора прискорення.
Дотичне прискорення Якщо Якщо ж
а) Рис 8.20 б) При Нормальне прискорення дорівнює нулю при прямолінійному русі ( Радіус кривини траєкторії можна визначити за формулою:
Зазначимо, що для обчислення дотичного прискорення Якщо рух точки задано координатним способом, у випадку опису руху в декартових координатах
Для полярних координат одержимо:
Окремі випадки руху точки при натуральному способі опису руху
Рівнозмінний рух точки
Якщо Встановимо закон зміни швидкості і закон руху точки по траєкторії при рівнозмінному русі. Оскільки.
Сталу інтегрування С1, знайдемо, виходячи з початкових умов. Нехай, наприклад, при t = О,
Так як Звідки, інтегруючи, одержимо:
Нехай, наприклад, при t = 0
Прямолінійний рух точки
Якщо траєкторія точки є прямою лінією, то направляючи одну з координат осей, наприклад, вісь х, вздовж цієї прямої, ми повністю визначимо положення точки заданням її абсциси як функції часу, тобто х = x(t). Проекції швидкості і прискорення точки на вісь х згідно формул (8.20) і (8.33) будуть
Модулі швидкості і прискорення відповідно рівні:
Якщо
де α,ω,ε - постійні величини. Рух точки за таким законом називають гармонійним. Величина α, що дорівнює максимальному відхиленню точки від положення х = 0, називається амплітудою коливань; Швидкість і прискорення точки, що здійснює гармонійне коливання, відповідно будуть
З формули для Рух за гармонійним законом буде періодичним рухом, тобто через рівні проміжки часу буде повністю повторюватись. Найменший проміжок часу, після закінчення якого рух повторюється, називається періодом коливань. Якщо позначити через Т період коливань, то буде справедлива рівність:
звідки
Кількість коливань за одиницю часу називається частотою коливань і дорівнює Питання для самоконтролю
1. Що означає рух точки? 2. Як визначається рівняння траєкторії при координатному способі опису руху? 3. Яка існує залежність між елементом дугової координати і елементом шляху? 4. Чи можна, знаючи закон руху точки по траєкторії, визначити траєкторією? 5. Коли перед інтегралом для визначення дугової координати необхідно брати "+" і коли "-"? 6. Що називається годографом вектора? 7. Як направлена похідна вектора за скалярним аргументом? 8. Яка існує залежність між радіусом-вектором точки, що рухається. і вектором швидкості цієї точки? 9. Чому дорівнюють проекції швидкостей на декартові осі координат? 10. Рух точки описаний полярними координатами. Як виражаються проекції швидкості на радіальний і поперечний напрямок? 11. Як виражається модуль вектора швидкості точки при натуральному способі опису руху? 12. Яка існує залежність між радіусом-вектором і прискоренням точки? 13. Чому дорівнюють проекції прискорення на осі декартової системи координат? 14. Які осі називаються натуральними? Що таке стична площина? 15. Чому дорівнюють проекції прискорення на дотичну, головну нормаль і бінормаль? 16. Який напрямок має вектор 17. Яку зміну швидкості характеризують нормальне і дотичне прискорення? 18. Як визначається кінематичний радіус кривини?
|
||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.195.180 (0.011 с.) |

 ,
, - одиничний вектор дотичної, направлений в сторону додатного відліку дуги;
- одиничний вектор дотичної, направлений в сторону додатного відліку дуги;  - проекція швидкості на напрям
- проекція швидкості на напрям 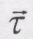 .
. (8.44)
(8.44) у вигляді:
у вигляді: (8.45)
(8.45)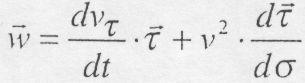 (8.46)
(8.46)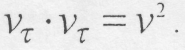
 . Вектор
. Вектор 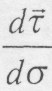 перпендикулярний вектору
перпендикулярний вектору  . Оскільки похідна вектора постійної довжини перпендикулярна вектору. Отже, вектор
. Оскільки похідна вектора постійної довжини перпендикулярна вектору. Отже, вектор  направлений по якійсь нормалі.
направлений по якійсь нормалі. - в положенні М1, переносячи вектор
- в положенні М1, переносячи вектор  в точку М. знайдемо зміну вектора
в точку М. знайдемо зміну вектора 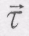 за проміжок часу
за проміжок часу 

 при русі точки в напрямку додатного відліку дуги направлений в бік ввігнутості траєкторії (рис. 8.19,а), а при русі точки в бік від'ємного відліку дуги - направлений в бік випуклості траєкторії (рис. 8.19,6).
при русі точки в напрямку додатного відліку дуги направлений в бік ввігнутості траєкторії (рис. 8.19,а), а при русі точки в бік від'ємного відліку дуги - направлений в бік випуклості траєкторії (рис. 8.19,6).

 буде завжди направлений в бік ввігнутості траєкторії (рис. 1.19, а і б), тому що при
буде завжди направлений в бік ввігнутості траєкторії (рис. 1.19, а і б), тому що при 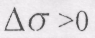 вектор
вектор  направлений протилежно вектору
направлений протилежно вектору  , при
, при  він направлений в той самий бік, що і вектор
він направлений в той самий бік, що і вектор  . Вектор
. Вектор  і
і  (площина МАВ).
(площина МАВ). лежить в стичній площині, оскільки при
лежить в стичній площині, оскільки при  площина МАВ збігається з стичною площиною в точці М.
площина МАВ збігається з стичною площиною в точці М. лежить в стичній площині, направлений в бік ввігнутості траєкторії, перпендикулярний до
лежить в стичній площині, направлений в бік ввігнутості траєкторії, перпендикулярний до  , отже, він направлений по головній нормалі до центра кривини.
, отже, він направлений по головній нормалі до центра кривини. . Трикутник АМВ рівнобічний (рис. 8.19,а), отже,
. Трикутник АМВ рівнобічний (рис. 8.19,а), отже, або користуючись рівняннями (8.43) і (1.44). одержимо:
або користуючись рівняннями (8.43) і (1.44). одержимо:
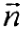 одиничний вектор головної нормалі, будемо мати:
одиничний вектор головної нормалі, будемо мати: і, отже
і, отже (8.47)
(8.47) і
і 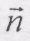 відповідно будуть:
відповідно будуть: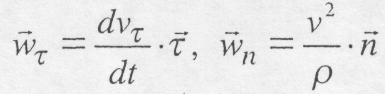

 (8.48)
(8.48)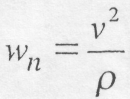 (8.49)
(8.49) . Проекція прискорення на бінормаль дорівнює нулю.
. Проекція прискорення на бінормаль дорівнює нулю.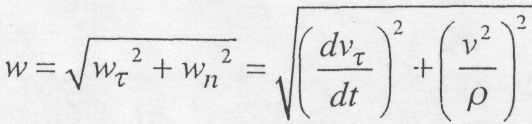 (8.50)
(8.50) дорівнює нулю при русі точки з постійною за модулем швидкістю і в момент часу, в якій швидкість
дорівнює нулю при русі точки з постійною за модулем швидкістю і в момент часу, в якій швидкість 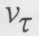 досягає екстремальних значень.
досягає екстремальних значень.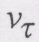 і
і  одного знака, то модуль швидкості
одного знака, то модуль швидкості  точки зростає і рух в цьому випадку називається прискореним (рис. 8.20а).
точки зростає і рух в цьому випадку називається прискореним (рис. 8.20а). спадає і рух буде сповільненим (рис. 8.20 б).
спадає і рух буде сповільненим (рис. 8.20 б).

 модуль швидкості залишається постійним і рух буде рівномірним.
модуль швидкості залишається постійним і рух буде рівномірним. J, а також в точках перегину криволінійної траєкторії і в моменти часу, при якому швидкість точки дорівнює нулю.
J, а також в точках перегину криволінійної траєкторії і в моменти часу, при якому швидкість точки дорівнює нулю. (8.51)
(8.51)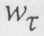 можна використати рівність
можна використати рівність  , оскільки
, оскільки 
 то будемо мати:
то будемо мати: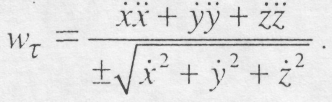

 - постійна величина, то рух точки називається рівнозмінним.
- постійна величина, то рух точки називається рівнозмінним. , то
, то  і
і 
 , тоді
, тоді  . Закон зміни швидкості прийме вигляд:
. Закон зміни швидкості прийме вигляд: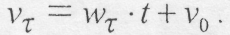 (8.52)
(8.52)

 , тоді
, тоді  і закон руху точки по заданій траєкторії буде мати вигляд:
і закон руху точки по заданій траєкторії буде мати вигляд: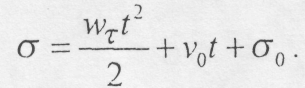 (8.53)
(8.53)

 , точки проходить в бік додатнього напрямку осі x. Якщо при цьому
, точки проходить в бік додатнього напрямку осі x. Якщо при цьому  , то рух буде прискорений, якщо ж
, то рух буде прискорений, якщо ж  то рух сповільнений. При
то рух сповільнений. При  точка рухається в напрямку протилежному додатному напрямку осі x. Якщо при цьому
точка рухається в напрямку протилежному додатному напрямку осі x. Якщо при цьому  , то рух сповільнений, якщо ж
, то рух сповільнений, якщо ж 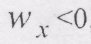 , то рух прискорений. Як приклад, розглянемо прямолінійний рух точки. За законом
, то рух прискорений. Як приклад, розглянемо прямолінійний рух точки. За законом ,
,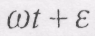 називається фазою і ε - початковою фазою коливань.
називається фазою і ε - початковою фазою коливань.
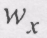 випливає, що прискорення точки завжди направлено до початку координат і за модулем пропорційне відхиленню точки від початку координат.
випливає, що прискорення точки завжди направлено до початку координат і за модулем пропорційне відхиленню точки від початку координат. ,
,
 . Якщо час вимірюється в секундах, то частота вимірюється в герцах. Кругова частота дорівнює кількості коливань за
. Якщо час вимірюється в секундах, то частота вимірюється в герцах. Кругова частота дорівнює кількості коливань за  одиниць часу.
одиниць часу. ?
?


