
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула моменту сили відносно точки в просторі.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
А). В). 23. Якщо кут між напрямком вісі та напрямком сили менше 900. А) Проекція вектора сили на вісь додатна. Б) Проекція вектора сили на вісь від’ємна. В) Момент сили відносно точки на площині додатний. Г) Момент сили відносно точки на площині від’ємний, Тема 2. КІНЕМАТИКА. Похідна за часом від радіуса-вектора точки дорівнює А) Швидкості точки. Б) Прискоренню точки. В) Кутовій швидкості тіла Г) Кутовому прискоренню тіла 25. Залежність координати точки від часу має вигляд: А) 26. Кутова швидкість обертання тіла-це: А) Осі, що переміщуються із рухомою точкою називаються А. координатними Б. векторними В. нормальними Г. натуральними 28. Вектор дотичного прискорення точки направлений: А. по головній нормалі до радіусу кривизни траєкторії Б. до початку відліку руху точки В. до кінцевого положення точки Г. по дотичній до траєкторії точки Нормальне прискорення спрямоване А. по дотичній до траєкторії Б. до початку відліку В. до початкового положення точки Г. по головній нормалі до центру кривизни Радіус кривизни при прямолінійному русі дорівнює А. нулю Б. дотичному прискоренню В. швидкості Г. нескінченності Лінійна швидкість точки, що рухається по колу дорівнює А. відношенню кутової швидкості до радіуса обертання Б. відношенню радіуса до кутової швидкості обертання В. кутовій швидкості Г. добутку кутової швидкості і радіуса обертання Величина, що характеризує швидкість зміни кутової швидкості називається А. нормальним прискоренням Б. дотичним прискоренням В. повним прискоренням Г. кутовим прискоренням При обертальному русі тіла, нормальне прискорення точки тіла дорівнює А. першій похідній зміни кутової швидкості за часом Б. першій похідній зміни кута повороту за часом В. добутку кутової швидкості і радіуса обертання Г. добутку радіуса обертання і квадрату кутової швидкості Дотичне прискорення точки тіла при обертальному русі тіла дорівнює А. першій похідній зміни кутової швидкості за часом Б. першій похідній зміни кута повороту за часом В. добутку радіуса обертання і квадрата кутової швидкості Г. добутку радіуса обертання і кутового прискорення Повне прискорення точки тіла при його обертальному русі дорівнює А. арифметичній сумі дотичного та нормального прискорень Б. сумі квадратів дотичного та нормального прискорень В. дотичному прискоренню Г. квадратному кореню з суми квадратів дотичного та нормального прискорень Якщо при русі будь-яка пряма, проведена в тілі переміщується паралельно сама собі, то такий рух називається А. прямолінійним Б. рівномірним В. обертовим Г. поступальним Рух тіла, при якому принаймі дві точки тіла нерухомі називається А. прямолінійним Б. паралельним В. рухом по колу Г. обертальним При плоскому русі тіла швидкості його точок А. визначаються добутком кутової швидкості на кут повороту тіла. Б. однакові по всьому тілу. В. визначаються за допомогою миттєвого центру швидкостей. Г. визначаються за теоремою про прискорення. Миттєвим центром швидкостей називається А. точка на плоскій фігурі, швидкість якої мінімальна Б. точка на плоскій фігурі, швидкість якої максимальна В. будь-яка точка плоскої фігури Г. точка плроскої фігури, швидкість якої дорівнює нулю Якщо на фігурі існує точка, швидкість якої дорівнює нулю, то вона називається А. опорою Б. реакцією В. проекцією Г. миттєвим центром швидкостей Миттєвий центр швидкостей двох точок знаходиться А. у точці, швидкість якої максимальна Б. у точці, швидкість якої мінімальна В. у будь-якій точці Г. у точці перетину перпендикулярів, відновлених до векторів швидкостей точок Миттеєвий центр швидкостей колеса, що котиться по твердій поверхні без просковзування знаходиться А. на осі колеса Б. у точці, протилежній точці контакту колеса з поверхнею В. у точці, що знаходиться у будь-якому місці по контуру Г. у точці контакту колеса з поверхнею
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 563; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.029 с.) |

 ; Б).
; Б). 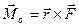 ;
; ; Г).
; Г). 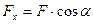 .
. . Записати рівняння залежності проекції вектора швидкості від часу.
. Записати рівняння залежності проекції вектора швидкості від часу.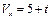 Б)
Б)  В)
В)  Г)
Г) 
 Б)
Б) 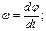 В)
В)  Г)
Г) 



