
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометричний та механічний зміст похідної. Дотична до кривої.Содержание книги
Поиск на нашем сайте
ГЕОМЕТРИЧНИЙ ТА МЕХАНІЧНИЙ ЗМІСТ ПОХІДНОЇ.ДОТИЧНА ДО КРИВОЇ. Механічний зміст похідної: похідна S`(t) є величиною миттєвої швидкості в момент t тіла, що рухається за законом S=S(t)/ Геометричний зміст похідної: похідна f`(x) дорівнює кутовому коефіцієнту дотичної до графіка функції у=f(x) в точці з абсцисою х. Рівняння дотичної до графіка функції у=f(x) у точці з абсцисою У=
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ
1.В якій точці дотична до графіка функції у=
2.При якому значенні а крива у=
3.Скласти рівняння дотичної до параболи у=
4.Два тіла рухаються прямолінійно: одне згідно закону ЗВ'ЯЗОК МІЖ НЕПЕРЕРВНІСТЮ ТА ДИФЕРЕНЦІЙОВНІСТЮ ФУНКЦІЙ.
ТЕОРЕМА. Якщо функція у=f(х) диференційовна в деякій точці неперервна.
НАСЛІДОК.З цієї теореми випливає, що неперервність функції є необхідною умовою Диференційовності функції. Це означає, що в точках розриву функція не має похідних, тобто вона не диференційовна. ОСНОВНІ ТЕОРЕМИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ. ПРАВИЛО ЛОПІТАЛЯ.
Теорема Лагранжа. Якщо функція у=f(x) неперервна на [a,b] і має похідну в усіх точках інтервала (а;b), то всередині цього інтервалу існує хоч би одна точка с (а <c<b) така,що виконується рівність
Теорема Ролля. Якщо функція у=f(x) неперервна на відрізку [a;b],диференційовна в усіх внутрішніх точках цього відрізка,а на його кінцях приймає рівні значен- ня.то похідна f`(x) дорівнює нулю хоч би в одній внутрішній точці с (a<c<b) цього відрізка. Правило Лопіталя. Нехай f(x) та g(x)-неперервні та мають похідні в усіх х ки х=а,а в точці а рівні нулю або нескінченності.Тоді границя відно- шення функцій дорівнює границі відношення їх похідних,якщо остання існує, тобто
Якщо відношення g`(x) задовільняють умовам правила Лопіталя, то для обчислення границі можна засто-совувати правило Лопіталя вдруге і т. д.
Приклад. Обчислити В данному випадку шення їх є невизначеністю вигляду одержуємо:
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ.
Обчислити границі:
1.
2.
3.
4.
Застосування диференціала до наближених обчислень
Головна частина приросту функції, яка лінійно залежить від приросту аргумента,називається диференціалом функції, позначається dy і обчислюється згідно формули dy=f`( Диференціал використовується для обчислення наближеного значення приросту функції
Приклад. Користуючись поняттям диференціала функції, знайти наближене значення приросту функції f(x)= Розв’язування.
Приклад. Знайти наближене значення функції у=
Розв’язування. f(x+ f(2)= dу=
Література. В.Т.Лисичкин, И.Л.Соловейчик. Математика. В.В.Барковський, Н.В.Барковська. Математика для економістів.
ІНДИВІДУАЛЬНІ СЕМЕСТРОВІ ЗАВДАННЯ
Знайти наближене значення приросту функції при заданій зміні аргументу
1. у= 2. у= 3.у= ln x при х=10 і 4.у= 5. у= 6. у= 7. у= 8. у= 9. у= 10. у=
Обчислити значення функцій
11. у= 12. у= 13. у= 14. у= 15. 16. 17. 18. 19. 20. 21. 22. 23.
ТЕМА 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ БАГАТЬОХ ЗМІННИХ.(10 ГОД.)
План.
1.Знаходження похідних вищих порядків функцій багатьох змінних. 2.Застосування повного диференціала функцій двох змінних для наближених обчислень. 3.Знаходження екстремумів функцій багатьох змінних. 4.Найбільше та найменше значення функції в замкнутій області. 5.Розв’язування завдань на знаходження умовного екстремуму функцій.
Література. В.В.Барковський, Н.В.Барковська.Математика для економістів. Ч.1. ст.238-257.
Застосування повного диференціала функцій двох змінних для наближених Обчислень.
Означення. Головна частина повного приросту функції двох змінних, яка лінійно залежить від z=f(x;y) і позначається dz або df(x;y). Отже, повний диференціал функції двох змінних можна знайти за допомогою формули dz= За допомогою диференціала можна знаходити наближене значення приросту функції
Приклад. Знайти наближене значення функції z=x
Розв'язування. z(1+0,03; 2-0,03) z(1;2)= 1
Z(1,03; 1,97)
ІНДИВІДУАЛЬНІ СЕМЕСТРОВІ ЗАВДАННЯ
Знайти наближене значення функцій в даній точці
1. z= х+3ху 2. z=x+x 3. z=x 4.z=x+2x 5.z=x 6.Z=2xy+y 7.z= x 8.z=x 9.z=4x 10.z=3x 11.z=x 12.z=x 13.z= x 14.z=x+3y 15.z=x 16. z=x 17. z=x 18. z= 2x+3y 19. z=x 20. z= x+2x 21.z=x+2x 22. z= 3x 23. z= 2x+x 24. z= x 25. z= 3x 26. z=x 27. z= 2x 28. z=x 29. z= x 30. z= 2x
Тема 4. РЯДИ. (14 ГОД.)
План. 1. Властивості збіжних рядів. 2. Ряд геометричноЇ прогресіЇ та гармонічний ряд. 3. Розв’язування завдань на знаходження області збіжності степеневих рядів. 4. Ряд Тейлора. Ряд Маклорена. 5. Розклад елементарних функцій у ряд Маклорена. 6. Застосування формули Тейлора для наближених обчислень.
Література. Барковський В.В.,Барковська Н. В. Математика для економістів. Вища математика.
ЗАВДАННЯ САМОСТІЙНОї РОБОТИ
Знайти область збіжності степеневих рядів
1. 2. ГЕОМЕТРИЧНИЙ ТА МЕХАНІЧНИЙ ЗМІСТ ПОХІДНОЇ.ДОТИЧНА ДО КРИВОЇ. Механічний зміст похідної: похідна S`(t) є величиною миттєвої швидкості в момент t тіла, що рухається за законом S=S(t)/ Геометричний зміст похідної: похідна f`(x) дорівнює кутовому коефіцієнту дотичної до графіка функції у=f(x) в точці з абсцисою х. Рівняння дотичної до графіка функції у=f(x) у точці з абсцисою У=
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ
1.В якій точці дотична до графіка функції у=
2.При якому значенні а крива у=
3.Скласти рівняння дотичної до параболи у=
4.Два тіла рухаються прямолінійно: одне згідно закону ЗВ'ЯЗОК МІЖ НЕПЕРЕРВНІСТЮ ТА ДИФЕРЕНЦІЙОВНІСТЮ ФУНКЦІЙ.
ТЕОРЕМА. Якщо функція у=f(х) диференційовна в деякій точці неперервна.
НАСЛІДОК.З цієї теореми випливає, що неперервність функції є необхідною умовою Диференційовності функції. Це означає, що в точках розриву функція не має похідних, тобто вона не диференційовна.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.77 (0.01 с.) |

 має вигляд
має вигляд
 паралельна осі абсцис.
паралельна осі абсцис.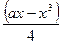 перетинає вісь Ох під кутом
перетинає вісь Ох під кутом  .
. в точці (3;4).
в точці (3;4). ,а друге – згідно закону
,а друге – згідно закону  .Знайти момент часу, коли швидкості цих тіл будуть рівними.
.Знайти момент часу, коли швидкості цих тіл будуть рівними. .
. а з околу точ-
а з околу точ- .
. знову є невизначеністю вигляду
знову є невизначеністю вигляду  або
або  і похідні f`(x) та
і похідні f`(x) та .
. та
та  задовольняють умовам правила Лопіталя.Відно-
задовольняють умовам правила Лопіталя.Відно-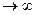 . Застосувавши правило Лопіталя,
. Застосувавши правило Лопіталя, .
.




 )
)  .
. та наближеного значення фукції f(x+
та наближеного значення фукції f(x+ 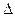 x)
x)  f(x)+dу.
f(x)+dу. при зміні аргумента х від 5 до 5,01.
при зміні аргумента х від 5 до 5,01.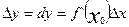 , f`(x)=
, f`(x)= 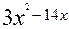 , f`(5)=
, f`(5)=  ,
,  .
.
 при х=2,004.
при х=2,004. =f(2,004)=f(2+0,004)
=f(2,004)=f(2+0,004) 
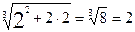
 , f`(2)=
, f`(2)= 
 0,004=0,002 f(2,004)=2+0,002=2,002.
0,004=0,002 f(2,004)=2+0,002=2,002. від 3 до 3.1
від 3 до 3.1 при х=3 і
при х=3 і 

 при х=2 і
при х=2 і 
 при х=3 і
при х=3 і  при х=1 і
при х=1 і  від 1 до 1.02
від 1 до 1.02 при х=2 і
при х=2 і 
 при х=3 і
при х=3 і 
 при х=2 і
при х=2 і  при х=10.03
при х=10.03 при х=3.002
при х=3.002 при х=24.99
при х=24.99 при х= 1.96
при х= 1.96
 24.
24. 
 25.
25. 
 26.
26. 
 27.
27. 
 28.
28. 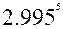
 29.
29. 
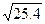 30.
30. 

 , називається повним диференціалом функції
, називається повним диференціалом функції .
.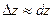 , а також знаходити наближене значення функції в заданій точці
, а також знаходити наближене значення функції в заданій точці .
. +2xy+y
+2xy+y  в точці М(1,03;1,97).
в точці М(1,03;1,97).
 =1+4+8=13
=1+4+8=13
 =
= 


 13+0,18-0,42= 12,76.
13+0,18-0,42= 12,76.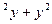 М(1,04; 1,96)
М(1,04; 1,96) М(1,06; 2,02)
М(1,06; 2,02) +2xy+y
+2xy+y  +xy М(2,03; 1,98)
+xy М(2,03; 1,98) x+y
x+y 




