
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знаходження умовного екстремуму методом Лагранжа .Содержание книги
Поиск на нашем сайте
Екстремум функціЇ Z=f(х;у) при виконанні умови екстремумом функціЇ. Умовні екстремуми часто використовуються при дослідженні опти, економічних та соціальних проблем. Для знаходження умовного екстремуму методом Лагранжа необхідно:
1.Записати функцію Лагранжа вигляду L(x,y, 2.знайти критичні точки М умови існування екстремуму:
3.перевірити в кожній критичній точці достатні умови існування екстремуму: а) якщо в точці М
Додатний, тоді точка Mk є точкою максимуму і
Б) якщо визначник
Приклад 9. Знайти екстремум функції Розв'язування. Будемо шукати умовний екстремум з використанням функції Лагранджа
Необхідні умови існування тепер мають вигляд
Виключаючи з цієї системи λ, одержимо:
Отже критичними точками будуть:
Для перевірки достатніх умов існування екстремуму запишемо визначник в довільній точці M(x,y), враховуючи
Тепер можна знайти значення цього визначника в кожній критичній точці і використати достатні умови:
ЗАВДАННЯ САМОСТІЙНОЇ РОБОТИ
Знайти умовні екстремуми функцій: 1) 2)
Тема 3. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ. (22 ГОД.)
План.
1. Первісна. Основна властивість первісноЇ. 2. Невизначений інтеграл. Властивості невизначеного інтегралу. Таблиця інтегралів. 3. Знаходження невизначених інтегралів різними методами. 4. Означення визначеного інтегралу та його геометричний зміст. 5. Властивості визначеного інтегралу. Формула Ньютона- Лейбніца. 6. Обчислення визначених інтегралів за допомогою формули прямокутників. 7. Обчислення визначених інтегралів за допомогою формули трапецій. 8. Обчислення площ фігур, обмежених даними лініями. 9. Розв’язування завдань на знаходження подвійних інтегралів.
Література. Барковський В.В., Барковська Н.В. Математика для економістів. Вища математика. Валуце І.І., Дилигул Г.Д. Математика для технікумів. Лисичкін В.В., Соловейчик І. Л. Математика.
Індивідуальні семестрові завдання Знайти інтеграли:
Обчислення визначених інтегралів за допомогою формул прямокутників
Нехай, наприклад, на кожному з відрізків
Отже,
Якщо ж значення ступінчатої функції на кожному з відрізків
Формули (1) і (2) називаються формулами прямокутників. Приклад: Обчисліть Розділимо відрізок
За формулою прямокутників (2) отримаємо:
Обчислення визначених інтегралів за допомогою формул трапецій При обчисленні інтегралу
В цьому випадку площа криволінійної трапеції
Отже,
Формула (3) називається формулою трапецій. Приклад: Обчисліть Розділимо відрізок
Завдання самостійної роботи 1. Обчисліть за формулами прямокутників наближене значення інтегралу:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.164 (0.008 с.) |

 (х;у)=0 називають умовним
(х;у)=0 називають умовним мізації багатьох
мізації багатьох (x,y)
(x,y) (х
(х  ) функції Лагранжа, використовуючи необхідні
) функції Лагранжа, використовуючи необхідні
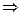

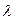
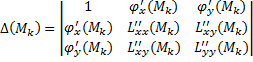

 , тоді точка Mk є точкою мінімуму і
, тоді точка Mk є точкою мінімуму і 
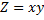 при умові, що
при умові, що 


 →
→  →
→ 
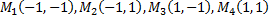
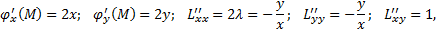

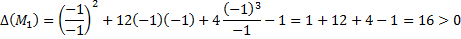



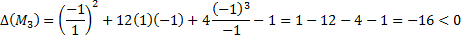


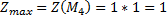
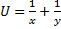 при
при 
 при
при 



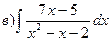

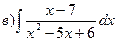

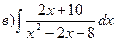















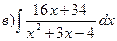










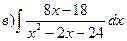


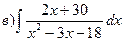



 При обчисленні інтегралу
При обчисленні інтегралу 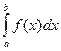 за формулами прямокутників підінтегральна функція
за формулами прямокутників підінтегральна функція  заміняється «ступінчатою функцією», яка на кожному з відрізків
заміняється «ступінчатою функцією», яка на кожному з відрізків  має стале значення, рівне значенню функції
має стале значення, рівне значенню функції 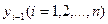 . Тоді площа криволінійної трапеції
. Тоді площа криволінійної трапеції 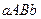 (а відповідно, і значення шуканого інтеграла) вважається наближено рівній сумі площ прямокутників з висотами
(а відповідно, і значення шуканого інтеграла) вважається наближено рівній сумі площ прямокутників з висотами  і основами
і основами  :
: .
. . (1)
. (1)
 . (2)
. (2) за формулами прямокутників.
за формулами прямокутників. на
на  частин. Тоді
частин. Тоді  . Складаємо таблицю значень підінтегральної функції.
. Складаємо таблицю значень підінтегральної функції.



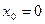
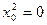


















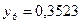


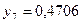









 За формулою прямокутників (1) отримаємо:
За формулою прямокутників (1) отримаємо:


 .
.
 і висотою
і висотою 
 (3)
(3) За формулою трапецій (3) отримаємо:
За формулою трапецій (3) отримаємо: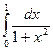 при
при  при
при 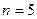 з чотирма десятковими знаками.
з чотирма десятковими знаками.


