
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціювання функції комплексної змінноїСодержание книги
Поиск на нашем сайте
1. Означення похідної. Умови Коші–Рімана. Похідною від функції комплексної змінної називається границя відношення приросту функції до приросту аргументу при прямуванні приросту аргументу до нуля:
Тут важливим є те, що ця величини не повинна залежати від способу прямування приросту аргументу Теорема 1.3. Якщо функція
Доведення: За умовами теореми існує границя (1.1), яка не залежить від способу прямування Припустимо, що
З існування границі даного комплексного співвідношення випливає, що існують і границі відповідно його дійсної і уявної частини. Тому в точці
Припускаючи, що
= Справедливими є обидві формули для Теорема 1.4. Якщо в точці Функція Для того, щоб перевірити функцію на аналітичність, потрібно переконатись що для її дійсної та уявної частини виконуються умови Коші – Рімана і частинні похідні від функцій 2. Властивості аналітичних функцій. 10 Нехай функції 20 Функція складена з аналітичних функцій є аналітичною. 30Якщо пряма функція є аналітичною при z є G, то обернена функція є теж аналітичною функцією, за винятком точок, в яких модуль похідної функції рівний нулю 40 Якщо відомою є дійсна частина аналітичної функції, то уявну частину цієї функції можна знайти з точністю до константи і, навпаки, якщо відома уявна частина цієї функції то її дійсну частину можна знайти з точністю до константи. 50 Якщо U і V є дійсною і уявною частинами аналітичної функції то
3. Геометричний зміст похідної. Нехай функція
Виберемо такий спосіб прямування
Рис. 3. Так, як похідна
З точністю до величин більш високого порядку малості має місце рівність Відображення околу точки
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 298; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.77 (0.006 с.) |


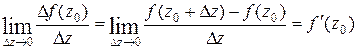 (1.1)
(1.1) до нуля.
до нуля. є диференційованою в точці
є диференційованою в точці  , то тоді в точці
, то тоді в точці  існують частинні похідні функцій
існують частинні похідні функцій 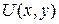 та
та  по змінних x, і y, причому мають місце наступні співвідношення:
по змінних x, і y, причому мають місце наступні співвідношення: ,
,  . (1.2)
. (1.2) (прямування здійснюється вздовж осі
(прямування здійснюється вздовж осі 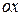 ), тоді:
), тоді: .
. , де
, де  ,
,  .
. (прямування
(прямування 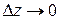 здійснюється вздовж осі
здійснюється вздовж осі  ), знаходимо:
), знаходимо: =
= .
. , отже переконуємось у справедливості співвідношень (1.2).
, отже переконуємось у справедливості співвідношень (1.2). є аналітичною в деякій області G, якщо в кожній точці цієї області функція
є аналітичною в деякій області G, якщо в кожній точці цієї області функція  і
і  є аналітичними в деяких областях z є G1, і z є G2, тоді
є аналітичними в деяких областях z є G1, і z є G2, тоді  ,
,  , є аналітичними в
, є аналітичними в  , а
, а  є теж аналітичною
є теж аналітичною 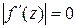 .
. .
.
 , де
, де 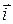 та
та  – одиничні вектори, тобто:
– одиничні вектори, тобто: .
.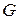 . Виберемо деяку точку
. Виберемо деяку точку  і проведемо через неї довільну криву
і проведемо через неї довільну криву  , яка повністю лежить в області
, яка повністю лежить в області  на деяку область
на деяку область  комплексної площини
комплексної площини  . Нехай точка
. Нехай точка 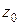 переходить в точку
переходить в точку  , а крива
, а крива 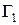 , що проходить через точку
, що проходить через точку  в точці
в точці  і представимо комплексне число
і представимо комплексне число  . (1.4)
. (1.4) лежать на кривій
лежать на кривій  лежать на кривій
лежать на кривій  відображаються векторами січних до кривих
відображаються векторами січних до кривих  і
і  мають геометричній зміст кутів відповідних векторів зі додатними напрямками осей
мають геометричній зміст кутів відповідних векторів зі додатними напрямками осей  та
та  , а
, а  і
і  представляють собою довжини цих векторів. При
представляють собою довжини цих векторів. При  , тобто аргумент
, тобто аргумент  похідної має геометричний зміст різниці кута
похідної має геометричний зміст різниці кута  вектора дотичної до кривої
вектора дотичної до кривої  вектора дотичної до кривої
вектора дотичної до кривої 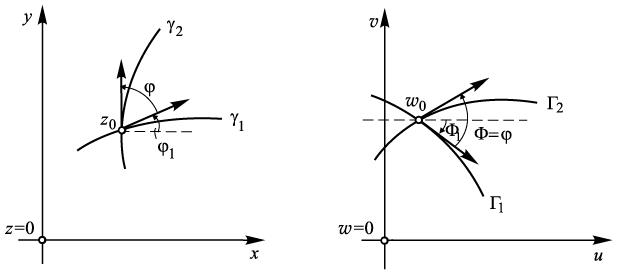
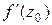 не залежить від способу граничного переходу, то ця різниця буде тією ж для довільної іншої кривої, яка проходить через точку
не залежить від способу граничного переходу, то ця різниця буде тією ж для довільної іншої кривої, яка проходить через точку  між довільними кривими
між довільними кривими  , які перетинаються в точці
, які перетинаються в точці  між їх образами (кривими
між їх образами (кривими 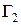 ), що пересікаються в точці
), що пересікаються в точці  . Ця властивість даного відображення носить назву властивості збереження кутів. Аналогічно із співвідношення (1.4) отримаємо:
. Ця властивість даного відображення носить назву властивості збереження кутів. Аналогічно із співвідношення (1.4) отримаємо: .
. . Геометричний зміст цього співвідношення полягає в тому, що при відображенні, що здійснюється аналітичною функцією за умови, що
. Геометричний зміст цього співвідношення полягає в тому, що при відображенні, що здійснюється аналітичною функцією за умови, що  визначає коефіцієнт перетворення подібності. Ця властивість даного відображення носить назву властивості постійного розтягу.
визначає коефіцієнт перетворення подібності. Ця властивість даного відображення носить назву властивості постійного розтягу.


