
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтеграли по комплексній зміннійСодержание книги Поиск на нашем сайте
1. Означення та основні властивості. Нехай на комплексній площині Нехай в кожній точці
де Якщо при
Записавши, що
Властивості інтегралів по комплексній змінній: 10 20 30 40 50 60 2. Теорема Коші. Оскільки значення контурного інтегралу залежить від напрямку інтегрування, домовимось в якості додатного напрямку обходження контуру брати напрям, при якому внутрішня область обмежена даним контуром, залишається зліва при обході контуру. Інтегрування в додатному напрямку будемо позначати через символ
Теорема 1.5 (теорема Коші). Нехай в однозв'язній області Доведення: Згідно з формулою (1.7):
Так як функція
що і треба було довести. Теорема 1.6 (друге формулювання теореми Коші). Якщо функція
Теорема 1.7 (третє формулювання теореми Коші). Нехай функція Доведення: Проведемо гладкі криві
Рис. 4. 3. Невизначений інтеграл. Важливим наслідком теореми Коші є наступне положення. Нехай функція
Теорема 1.8. Нехай функція
(1.9) – формула Ньютона – Лейбніца. Це за умови, що
Інтеграл Коші 1. Виведення формули Коші. Нехай функція
Функція
Змінивши напрямок інтегрування в другому інтегралі, цю рівність можна переписати у вигляді:
Оскільки інтеграл, що знаходиться зліва, не залежить від вибору контуру
Рис. 5. Підставивши
Інтеграл справа перетворимо так:
Спрямуємо
Так, як у формулі (1.11) останній доданок не залежить від
Інтеграл, що стоїть у правій частині формули (1.12), виражає значення аналітичної функції
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.139 (0.009 с.) |

 задана кусково-гладка крива
задана кусково-гладка крива  кінцевої довжини
кінцевої довжини  . Використовуючи параметричне представлення кривої
. Використовуючи параметричне представлення кривої  і
і  кожної її точки рівність
кожної її точки рівність  ,
,  , де
, де  і
і  кусково-гладкі функції дійсного параметра
кусково-гладкі функції дійсного параметра 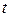 , який змінюється в межах
, який змінюється в межах  (
( і
і  можуть відповідно набувати значення ±
можуть відповідно набувати значення ±  ), що задовольняють умову
), що задовольняють умову 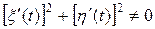 . Задання координат
. Задання координат  дійсної змінної
дійсної змінної  кривої
кривої  . Розіб’ємо криву
. Розіб’ємо криву  частинних дуг точками ділення
частинних дуг точками ділення  , що відповідають зростаючим значенням параметру
, що відповідають зростаючим значенням параметру  ). Введемо позначення
). Введемо позначення  та складемо суму:
та складемо суму: , (1.5)
, (1.5)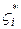 – деяка точка і-той частинної дуги.
– деяка точка і-той частинної дуги. існує границя сум (1.5), яка не залежить від способу розбиття кривої
існує границя сум (1.5), яка не залежить від способу розбиття кривої  . (1.6)
. (1.6)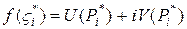 ,
,  , де
, де  – точка кривої
– точка кривої  ,
,  ми можемо представити (1.5) вираження у вигляді:
ми можемо представити (1.5) вираження у вигляді: .
. . (1.7)
. (1.7) ;
; ;
; ;
; , де
, де  – елемент довжини дуги;
– елемент довжини дуги; , де
, де  ;
; .
. або просто
або просто  , а інтегрування у від’ємному напрямку через –
, а інтегрування у від’ємному напрямку через –  . Властивості інтегралів по замкнутому контуру від аналітичних функції всередині області, що обмежена даним контуром визначаються відомими властивостями криволінійних інтегралів першого роду. Як відомо для криволінійних інтегралів по замкнутому контурі має місце наступне твердження: якщо функції
. Властивості інтегралів по замкнутому контуру від аналітичних функції всередині області, що обмежена даним контуром визначаються відомими властивостями криволінійних інтегралів першого роду. Як відомо для криволінійних інтегралів по замкнутому контурі має місце наступне твердження: якщо функції  і
і 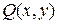 неперервні в замкнутій області
неперервні в замкнутій області  , яка обмежена кусочно гладким контуром
, яка обмежена кусочно гладким контуром 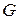 , то:
, то: . (1.8)
. (1.8) . Тоді інтеграл від цієї функції по довільному замкнутому контуру
. Тоді інтеграл від цієї функції по довільному замкнутому контуру  , що повністю лежить в цій області, рівний нулю.
, що повністю лежить в цій області, рівний нулю. .
.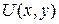 та
та  в області, яка є обмежена цим контуром, володіють неперервними частинними похідними першого порядку. Тому до криволінійних інтегралів, що стоять зліва можна застосувати формулу (1.8):
в області, яка є обмежена цим контуром, володіють неперервними частинними похідними першого порядку. Тому до криволінійних інтегралів, що стоять зліва можна застосувати формулу (1.8):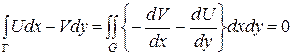 ,
, ,
,
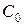 , а в середині контурами
, а в середині контурами  і нехай функція неперервна в замкнутій області
і нехай функція неперервна в замкнутій області  , причому обхід границі
, причому обхід границі  , що з'єднують контур
, що з'єднують контур 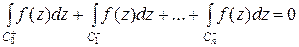 .
.
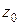 і позначимо через
і позначимо через  інтеграл по довільній кривій, що повністю лежить в області
інтеграл по довільній кривій, що повністю лежить в області  .
. (
( ) є аналітичною функцією в області
) є аналітичною функцією в області  (без доведення).
(без доведення). . (1.9)
. (1.9) – не виходить за межі області аналітичності функції.
– не виходить за межі області аналітичності функції. . ( 1.9 )
. ( 1.9 ) , очевидно, є аналітичною функцією у всіх точках області
, очевидно, є аналітичною функцією у всіх точках області  , який лежить в середині
, який лежить в середині  , яка є замкнутою між контурами
, яка є замкнутою між контурами  рівний нулю:
рівний нулю: .
. . (1.10)
. (1.10) з радіусом
з радіусом  і центром в точці
і центром в точці 
 , то отримаємо:
, то отримаємо: .
.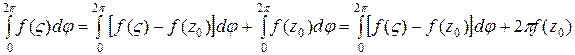 . (1.11)
. (1.11) можна поставити таке значення
можна поставити таке значення  , для
, для  . Звідси випливає, що при
. Звідси випливає, що при  існує границя:
існує границя: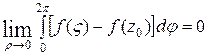 .
. , а відповідно,
, а відповідно,  , то згідно (1.10):
, то згідно (1.10): . (1.12)
. (1.12)


