
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Натуральні логарифми. Границя, пов’язана з натуральним логарифмомСодержание книги
Поиск на нашем сайте
Розглянемо функцію
Нехай Припустимо, що точка Означення. Граничне положення січної Позначимо через
Тепер звернемо увагу на положення графіка
Рис.26 В точці Можна довести, що значення шуканої основи Число Логарифми за основою
За формулою переходу до нової основи
маємо зв’язок між десятковими та натуральними логарифмами
Має місце формула
Дамо геометричне пояснення формули (2).
Згідно рис. 27 із
Якщо
Друга важлива границя Так називається рівність
За формулою (1) розкривається невизначенність вигляду Для доведення (1) перетворимо співвідношення (2) із 3.10.:
Перейшовши формально до границі під знаком логарифма в останній рівності, отримаємо
Замінимо в (2) Зауважимо, що перехід до границі під знаком логарифма ми здійснили формально. Для його строгого обгрунтування потрібно послатись на властивість неперервності цієї функції. Мова про це піде пізніше.
Приклади 1.
2.
3.
Приклади для самостійного розв’язання. 1. 4. 7. 10. Відповіді. 1. Порівняння нескінченно малих (н.м.)
Відомо, що дві сталі величини Означення 1. Якщо відношення
а, значить,
то Приклад. Функції
Означення 2. Якщо відношення двох н.м. дорівнює нулю, тобто
то Приклади. Нехай
Отже Означення 3. Н.м.
Приклад. Нехай
то Означення 4. Якщо границя відношення двох н.м.
то
Таблиця основних еквівалентних н.м.
1. 2. 3. 4. 5. Формули 1–7 були отримані в попередніх параграфах. Розглянемо останню.
= Наведена таблиця використовувається при розкритті невизначеностей. Нехай н.м. Теорема 1. Границя відношення двох н.м. функцій дорівнює границі відношення їх еквівалентних величин, тобто
Дійсно,
Приклад. 1.
Теорема 2. Якщо
то їх різниця Дійсно,
Теорему 2 треба мати на увазі при знаходженні границь. Розглянемо
Хоча
Тепер
Отже, згідно з означенням 3 можна зробити висновок, що
|
||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.60.19 (0.006 с.) |

 при
при  . Її область визначення:
. Її область визначення:  . Оскільки
. Оскільки  , графік проходить через початок координат (див. рис. 25)
, графік проходить через початок координат (див. рис. 25)
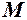 довільна точка графіка. Пряму
довільна точка графіка. Пряму  , що перетинає графік в двох точках
, що перетинає графік в двох точках  і
і  кут
кут  .
. . Січна
. Січна  називається дотичною до кривої
називається дотичною до кривої  кут нахилу дотичної, тоді згідно означення маємо
кут нахилу дотичної, тоді згідно означення маємо або
або  (1)
(1) . Для прикладу розглянемо функції
. Для прикладу розглянемо функції При
При  маємо
маємо 

 Схематично положення кривих
Схематично положення кривих  зображено на рис. 26
зображено на рис. 26
 цей кут збільшується. Очевидно, що можна підібрати основу
цей кут збільшується. Очевидно, що можна підібрати основу 
 , тобто, щоб дотичною стала бісектриса
, тобто, щоб дотичною стала бісектриса  .
. дорівнює ірраціональному числу
дорівнює ірраціональному числу  яке прийнято позначати буквою
яке прийнято позначати буквою 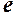 . Більш точно
. Більш точно  .
. пишуть
пишуть  .
.
 або
або 
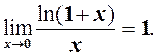 (2)
(2)
 маємо
маємо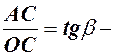 кутовий коефіцієнт січної, але
кутовий коефіцієнт січної, але  , тому
, тому
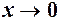 , то кут нахилу січної
, то кут нахилу січної  , тому у відповідності із співвідношенням (1)
, тому у відповідності із співвідношенням (1)  Звідки отримуємо (2).
Звідки отримуємо (2).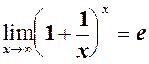 . (1)
. (1)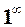 .
.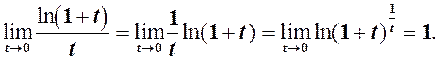
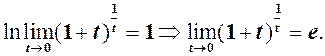
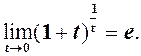 (2)
(2)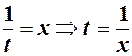 (при
(при 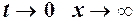 ) одержимо рівносильну рівність (1).
) одержимо рівносильну рівність (1).
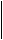

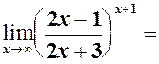 Виділяємо цілу частину =
Виділяємо цілу частину =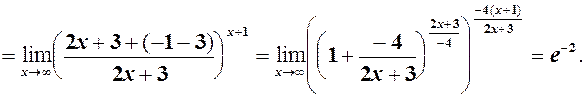

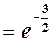 , оскільки
, оскільки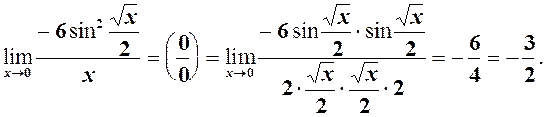
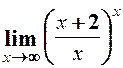 . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
. . 8.
. 8. 
 . 9.
. 9.  .
.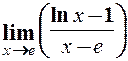 .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  і
і  можна порівнювати між собою або за допомогою дій віднімання (
можна порівнювати між собою або за допомогою дій віднімання ( ), або ділення
), або ділення  . При порівнянні н.м.
. При порівнянні н.м.  і
і  до згаданих операцій додається ще перехід до границі, коли
до згаданих операцій додається ще перехід до границі, коли  скінченне або
скінченне або  .
. двох нескінченно малих має скінченну границю
двох нескінченно малих має скінченну границю 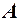 відмінну від нуля, тобто
відмінну від нуля, тобто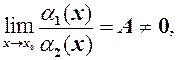

 і
і 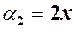 при
при 
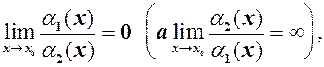
 а
а  і
і 
 є н.м. вищого порядку в порівнянні з
є н.м. вищого порядку в порівнянні з  . Це означає, що
. Це означає, що 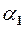 швидше зменшується ніж
швидше зменшується ніж 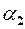 . Щоб оцінити степінь зменшення однієї н.м. в порівнянні з іншою, вводиться поняття порядку зміни.
. Щоб оцінити степінь зменшення однієї н.м. в порівнянні з іншою, вводиться поняття порядку зміни.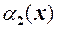 , якщо
, якщо  є н.м. одного порядку, тобто
є н.м. одного порядку, тобто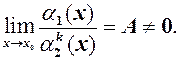
 а
а  Оскільки
Оскільки
 є н.м. другого порядку відносно
є н.м. другого порядку відносно 
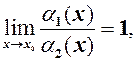
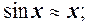 6.
6. 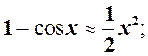
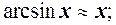 7.
7. 
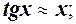 8.
8. 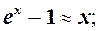
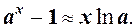
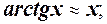
 Заміна
Заміна 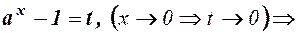 =
=
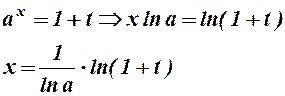
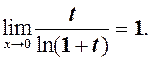
 і
і 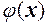 мають своїми еквівалентними
мають своїми еквівалентними 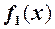 і
і 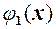 , тобто
, тобто 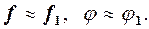 Тоді має місце теорема.
Тоді має місце теорема.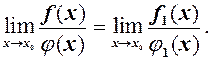
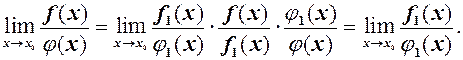
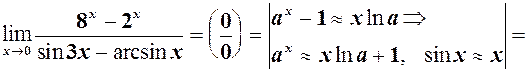

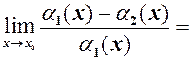
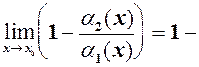
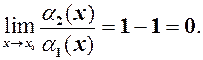
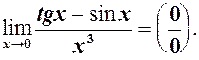
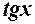 і
і 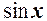 є н.м. першого порядку в порівнянні з
є н.м. першого порядку в порівнянні з 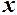 , їх різниця матиме більш високий порядок, тому використання таблиці
, їх різниця матиме більш високий порядок, тому використання таблиці 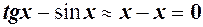 не допоможе. В даному випадку необхідно перетворити
не допоможе. В даному випадку необхідно перетворити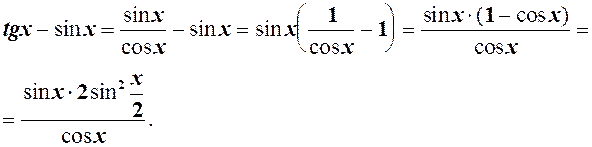
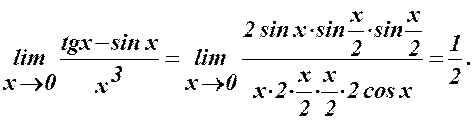
 є н.м. третього порядку в порівнянні з
є н.м. третього порядку в порівнянні з 


