
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теореми про існування границьСодержание книги Поиск на нашем сайте
Теорема 1. Нехай при
Якщо існують границі
Доведення. Очевидно, що із нерівності За теоремою 1 із 2.4. Теорема 2. Якщо функція
Рис. 23.
Аналогічне твердження має місце і для спадної, обмеженої знизу, функції
Односторонні границі
Будемо розглядати процес, коли змінна Означення. Число Аналогічно, якщо Ліва – і права границі називають односторонніми. Їх ще прийнято позначати
Зауваження. Рівності
еквівалентні Якщо ж односторонні границі різні, тобто
або хоча б одна з них не існує, тоді не існує й границя функції
3.7. Невизначеності. Приклади знаходження деяких границь При знаходженні границі ми використовуємо їх властивості, зокрема теорему 2 із 3.4. Можуть виникати такі випадки. 1. Якщо функція визначена в точці
тобто границя функції збігається з її значенням в точці 2. Якщо ж функція в точці
В більшості таких прикладів для знаходження границі над функціями, що стоять під знаком
1) за наслідками із 2.4 = тобто границя функції збігається з її значенням, бо
.
Зауваження. У загальному випадку, якщо
Це, зокрема, стосується випадку, коли
отримаємо
де Аналогічно для
тоді
4)
5)
3.8. Границя дробово раціональної функції при х ®¥
Розглянемо спочатку наступний приклад 7) = (добуток н.в. на обмежену є н.в.) = ¥. З даного прикладу можна зробити висновок, що у випадку многочлена із степенями різних знаків при
В кожній з дужок обмежені величини. Можливі три випадки: 1) 2)
Приклади для самостійного розв’язання Знайти границі. 1. 4. 7. 10. 12. 15. 18. 21. 24. 26. 28. 30. 32. 34. Відповіді. 1. 3. 2. 1. 3. 0. 4. -6. 5. 1/4. 6. -3. 7. 3/2. 8. 26.
Перша важлива границя
Першою важливою називається границя
Для доведення (1) будемо виходити із геометричних міркувань (див. рис. 24)
Оскільки
Із
За теоремою 1 із 2.5 про границю нерівностей маємо
що рівносильно (1). На основі (1) отримаємо ще кілька необхідних формул.
Аналогічно
Приклади. 1. 2.
3.
Приклади для самостійного розв’язання Знайти границі 1. 4. 7. 10. 13. 16. 18. 20. Відповіді. 1. 9. 17.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-28; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

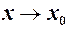 (
(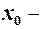 скінченне або
скінченне або 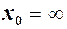 ) для трьох функцій виконується нерівність
) для трьох функцій виконується нерівність
 і
і  , які дорівнюють числу
, які дорівнюють числу 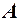 , то існує
, то існує .
.

 н.м.,
н.м.,  н.м. при
н.м. при 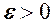 можна знайти
можна знайти  таке, що з нерівності
таке, що з нерівності 

 а, отже,
а, отже,  тобто
тобто 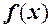 зростає, і якщо вона обмежена зверху, тобто
зростає, і якщо вона обмежена зверху, тобто  ,
,  то ця функція має границю
то ця функція має границю  , а
, а 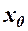 -скінчене або
-скінчене або  (див.рис.23).
(див.рис.23).
 .
. , але при цьому
, але при цьому 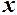 залишається меншим
залишається меншим 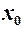 , тобто зліва. Цей факт позначають
, тобто зліва. Цей факт позначають 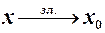 (зл. – зліва), або зручніше записувати
(зл. – зліва), або зручніше записувати 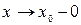 . Аналогічно, якщо
. Аналогічно, якщо 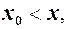 то будемо говорити, що
то будемо говорити, що 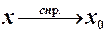 або
або  .
. називається лівою границею функції
називається лівою границею функції 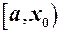 і для неї існує
і для неї існує 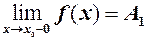 .
.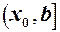 і існує
і існує 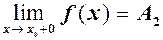 , то
, то 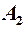 називається правою границею функції
називається правою границею функції 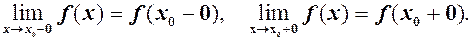
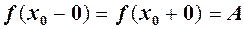
 , тобто якщо односторонні границі існують і рівні в точці
, тобто якщо односторонні границі існують і рівні в точці 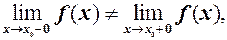
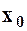 , то
, то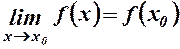 ,
,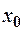 .
.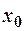 невизначена або
невизначена або  , то можуть зустрітись співвідношення вигляду:
, то можуть зустрітись співвідношення вигляду: 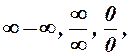
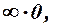
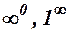 , які називаються невизначеностями.
, які називаються невизначеностями.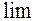 необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей.
необхідно виконати певні тотожні перетворення, або ще говорять: “позбавитися невизначеності” або “розкрити невизначеність”. А там, де невизначеності не зустрічаються, розв’язання здійснюються у відповідності теореми 2 та властивостей.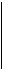 Розглянемо кілька конкретних прикладів з поясненнями
Розглянемо кілька конкретних прикладів з поясненнями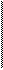 Знайти
Знайти 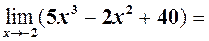 згідно теореми 2, а також =
згідно теореми 2, а також =
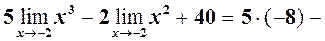
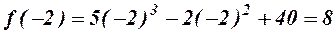 .
.
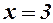 невизначена, і
невизначена, і 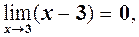 то теорему 2 не можна застосовувати. Робимо перетворення.
то теорему 2 не можна застосовувати. Робимо перетворення.
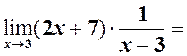
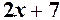 – обмежена
– обмежена
 – н.м., оберненна
– н.м., оберненна
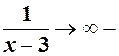 н.в., добуток їх – н.в.
н.в., добуток їх – н.в.
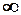

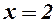 ф. невизначена
ф. невизначена
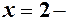 корінь чисельника і знаменника. Розклад на множники
корінь чисельника і знаменника. Розклад на множники
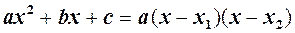
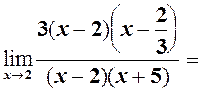
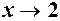 і,
і, 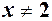 то на
то на  скорочуємо
скорочуємо
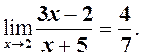
 то необхідно зробити тотожні перетворення так, щоб
то необхідно зробити тотожні перетворення так, щоб 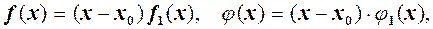 і тоді замість
і тоді замість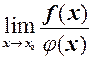 розглянути
розглянути 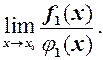
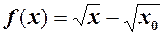 , тоді за допомогою тотожності
, тоді за допомогою тотожності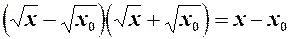 (1)
(1)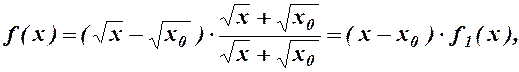
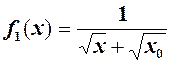 .
. береться тотожність
береться тотожність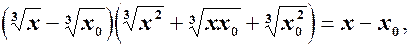 (2)
(2)

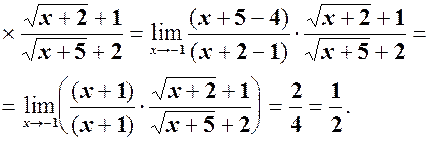
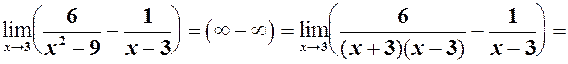
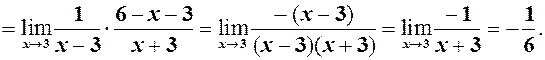

 6)
6) 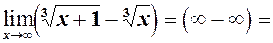 див. формулу (2) =
див. формулу (2) =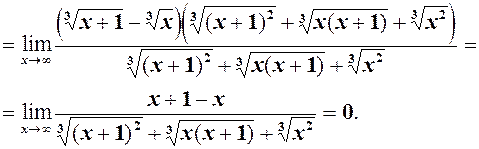

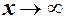 може бути невизначеність
може бути невизначеність 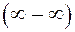 . Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при
. Щоб її розкрити необхідно винести старший степінь за дужки. Враховуючи цей висновок, розглянемо границю дробово раціональної функції (див. 1.9) при 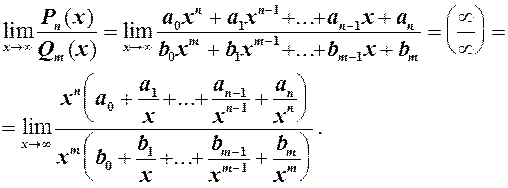
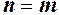 , тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях
, тоді степені скорочуються і границя дорівнює відношенню коефіцієнтів при старших степенях  ;
;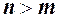 , тоді після скорочення в чисельнику залишиться
, тоді після скорочення в чисельнику залишиться  , тому границя дорівнює ¥;
, тому границя дорівнює ¥;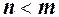 , тоді після скорочення в знаменнику залишиться
, тоді після скорочення в знаменнику залишиться 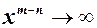 , а обернена до неї
, а обернена до неї  при
при 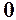 . Отже
. Отже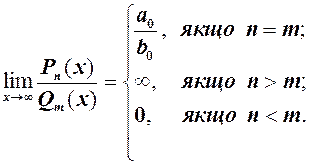 (1)
(1) . 2.
. 2.  . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9.  .
. . 11.
. 11. 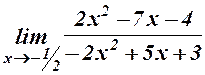 .
. . 13.
. 13.  . 14.
. 14.  .
. . 16.
. 16.  . 17.
. 17.  .
. . 19.
. 19.  . 20.
. 20.  .
. . 22.
. 22.  . 23.
. 23.  .
. . 25.
. 25.  .
. . 27.
. 27.  .
. . 29.
. 29.  .
. . 31.
. 31.  .
. . 33.
. 33.  .
. .
. . 9.
. 9.  . 10.
. 10.  . 11.
. 11.  . 12.
. 12.  . 13.
. 13.  . 14.
. 14.  . 15.
. 15.  . 16.
. 16.  . 17.
. 17.  . 19.
. 19.  . 20.
. 20.  . 21. 2/3. 22.
. 21. 2/3. 22.  . 23.
. 23.  . 24.
. 24.  . 27. 1/2. 28.
. 27. 1/2. 28.  . 32.
. 32.  . 34.
. 34. 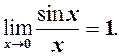 (1)
(1)
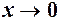 , то вважаємо, що кут 2
, то вважаємо, що кут 2 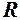 . Довжина хорди
. Довжина хорди 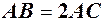 очевидно менша довжини дуги
очевидно менша довжини дуги 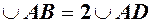 , а дуга
, а дуга 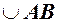 очевидно менша довжини ламаної
очевидно менша довжини ламаної 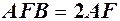 , тобто
, тобто

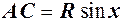 . Довжина дуги
. Довжина дуги 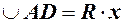 . Із
. Із 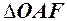 довжина дотичної
довжина дотичної 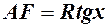 . Отже, нерівність запишеться
. Отже, нерівність запишеться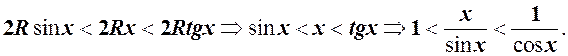
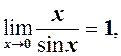
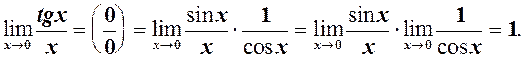
 . (2)
. (2)
 заміна
заміна 
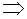

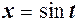 . Якщо
. Якщо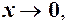 то
то 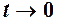
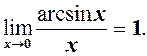 (3)
(3)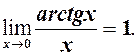 (4)
(4)
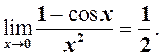 (5)
(5)

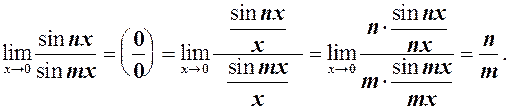
 Заміна
Заміна 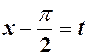 =
=
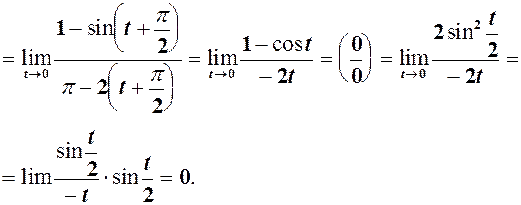

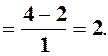
 . 2.
. 2. 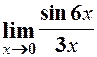 . 3.
. 3.  .
. . 5.
. 5.  . 6.
. 6.  .
. . 8.
. 8.  . 9.
. 9.  .
. . 11.
. 11.  . 12.
. 12.  .
. . 14.
. 14.  . 15.
. 15.  .
. . 17.
. 17.  .
. . 19.
. 19.  .
. .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  .
. . 10.
. 10.  . 16.
. 16.  .
. . 19.
. 19.  .
.


