
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додаток 15. Статистичні функціїСодержание книги
Поиск на нашем сайте
Імовірність. Функція доводить імовірність того, що значення з інтервалу знаходиться усередині заданих меж. Якщо верхню межу не задано, то виявляється ймовірність того, що значення в аргументі x інтервалу дорівнює значенням аргументу нижньої межі. Формат опису функції має такий вигляд: Вероятность (x_діап.; інтер_імовірностей; нижня_межа; верхня_межа), де X_діап. – це інтервал числових значень x, з якими зв'язані ймовірності. інтер_імовірностей – це множина ймовірностей, що відповідають значенням в аргументі x_діап. нижня_межа – це нижня межа значення, для якого обчислюється ймовірність. верхня_межа – це необов'язкова верхня межа значення, для якого потрібно обчислити ймовірність. Дисперсія за вибіркою характеризує розкид значень досліджуваної змінної навколо середнього значення. Формат опису має такий вигляд: ДИСП (число1; число2;...) Число1, число2,... – це кількість числових аргументів від 1 до 30, що відповідають вибірці з генеральної сукупності. ДИСП використовує таку формулу для обчислення дисперсії: Довірчий інтервал характеризуєдовірчий інтервал по обидва боки від середньої вибірки. Функція повертає довірчий інтервал для середньої генеральної сукупності. Формат опису функції має такий вигляд: ДОВЕРИТ (альфа; станд_откл; розмір), де альфа – це рівень значущості, що використовується для обчислення рівня надійності ((1 – альфа)●100%), якщо альфа дорівнює 0,05, то це означає 95-процентний рівень надійності; станд_откл – це стандартне відхилення генеральної сукупності для інтервалу даних, передбачається, що воно є відомим; розмір – це розмір вибірки. Коефіцієнт кореляції повертає коефіцієнт кореляції між двома інтервалами даних, які подано у вигляді масивів. Коефіцієнт кореляції використовується для визначення наявності взаємозв'язку між двома інтервалами даних. Формат опису функції має такий вигляд: КОРРЕЛ (масив1; масив2), де масив1 – перший інтервал осередків зі значеннями. масив2 – другий інтервал осередків зі значеннями. Рівняння для коефіцієнта кореляції має такий вигляд:
де Медіана – це число, що є серединою множини чисел, тобто половина чисел мають значення більші, ніж медіана, а половина – менші, ніж медіана. Функція повертає медіану заданих чисел. Формат опису функції має такий вигляд: МЕДИАНА (число1; число2;...), де число1, число2, … – це числа від 1 до 30, для яких визначається медіана. Мінімальне значення повертає найменше значення в списку аргументів. Формат опису функції має такий вигляд: МИН (число1; число2;...), де число1, число2,... — це числа від 1 до 30, серед яких шукається мінімальне значення. Мода повертає найбільше значення, яке часто зустрічається або повторюється в масиві або інтервалі даних. Так само, як і функція МЕДІАНА, функція МОДА є мірою взаємного розташування значень. Формат опису функції має такий вигляд: МОДА (число1; число2;...), де число1, число2, ... –це кількість аргументів від 1 до 30, для яких обчислюється мода. Можна використати один масив або одне посилання на масив замість аргументів, що розділяються крапкою з комою. Ранг числа характеризуєйого величину щодо інших значень у списку. Функція повертає ранг числа в списку чисел. Формат опису функції має такий вигляд: РАНГ (число; посилання; порядок), де число – це число, для якого визначається ранг; посилання – це масив або посилання на список чисел, нечислові значення в посиланні ігноруються; порядок – це число, що визначає спосіб упорядкування. Розподіл Стьюдента повертає процентні точки (імовірність) для t-розподілу Стьюдента, де числове значення x – це обчислене значення, для якого мають бути обчислені ймовірності. Цей розподіл використовується для перевірки при малому обсязі вибірки або замість таблиці критичних значень t-розподілу. Формат опису функції має такий вигляд: СТЬЮДРАСП (x; ступені_свободи; хвости), де х — це числове значення, для якого потрібно обчислити розподіл. ступені_свободи — ціле число, що вказує кількість ступенів свободи; хвости — кількість повертальних хвостів розподілу. Якщо хвости дорівнюють одиниці, то функція СТЬЮДРАСП повертає однобічний розподіл, якщо двом – двосторонній розподіл. Середнє значення повертає середнє (арифметичне) своїх аргументів. Формат опису функції має такий вигляд: СРЗНАЧ (число1; число2;...), де число1, число2, ... – це кількість аргументів від 1 до 30, для яких обчислюється середнє. Стандартне відхилення оцінює стандартне відхилення по вибірці. Стандартне відхилення – це міра того, наскільки широко розкидані точки даних відносно їхнього середнього. Формат опису функції має такий вигляд: СТАНДОТКЛ (число1; число2;...), де число1, число2, … – це кількість числових аргументів від 1 до 30, що відповідають вибірці з генеральної сукупності.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 271; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.208 (0.005 с.) |


 ,
,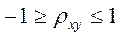 ;
;  .
.


