
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числова функція. Область визначення і множина значень функції. Способи завдання функції. Парні і непарні функції. Зростаючі та спадаючі функції. Періодичні функції.Содержание книги
Поиск на нашем сайте Числова функція. Область визначення і множина значень функції. Способи завдання функції. Парні і непарні функції. Зростаючі та спадаючі функції. Періодичні функції. Функцією називається залежність змінної у від змінної х, якщо кожному значенню х відповідає єдине значення у. У - залежна змінна (функція) Х - незалежна змінна (аргумент)
Властивості функції 1) областю визначення функції називається множина значень, яких приймає незалежна змінна х
2) областю значення функції називається множина значень, яких приймає залежна змінна у при відповідних значеннях х
Способи задання функції: 1) аналітичний спосіб – полягає у тому, що у виражають через х за допомогою формули. 2) графічний 3) табличний 4) словесний Парні і непарні функції
Зростаючі та спадаючі функції Функцію Функцію Періодичні функції Функція
2. Корінь п-го степеня. Арифметичний корінь п-го степеня, його властивості
3. Степеневі функції, їхні властивості та графіки
Показникова функція, її властивості та графіки. Функція виду Графіки показникової функції:
Перетворення графіків показникової функції 1) 2)
Із збільшенням коефіцієнта k точка перетину графіка з віссю ОУ переміщується догори і її ордината дорівнює k. Логарифм числа. Основна логарифмічна тотожність. Основні властивості логарифмів.
Логарифмом числа b (b>0) за основою а (
Формула переходу від показникової рівності до логарифмічної
Основна логарифмічна тотожність
Десятковим логарифмом називається логарифм, основа якого дорівнює 10. Властивості логарифмів 1) 2) 3) Логарифм добутку двох додатних множників дорівнює сумі їх логарифмів
4) логарифм частки двох додатніх виразів дорівнює різниці логарифмів діленого та дільника
5) логарифм степеня додатного числа дорівнює показнику степеня, помноженому на логарифм основи цього степеня
6) 7) формула переходу до іншої основи а) б) Логарифмуванням називається дія знаходження логарифма числа (виразу) Потенціювання – це дія знаходження числа (виразу) за його логарифмом.
Основні співвідношення між тригонометричними функціями
Р2(х,у) Рa( Рівняння кола з центром у початку координатної має вигляд:
Основна тригонометрична тотожність: «Золота одиниця»
Наслідки: 1) 2) 3) 4) Залежність між тангенсом і котангенсом:
Залежність між косинусом і тангенсом:
Залежність між синусом і котангенсом:
Косинус різниці двох кутів:
Косинус суми двох кутів:
Синус різниці двох кутів:
Синус суми двох кутів:
Тангенс різниці двох кутів:
Тангенс суми двох кутів:
Поняття похідної, її геометричний та фізичний зміст
Фізичний зміст похідної.
Поняття похідної. Правила диференціювання. Похідні основних елементарних функцій
Правила диференціювання. 1) Теорема: Якщо функції f(x) і g(x) диференційовані в точці х, то їхня сума диференційована в цій точці і (f(x)+g(x))'=f '(x)+g'(x) або коротко говорять: похідна суми дорівнює сумі похідних. Доведення: Розглянемо функцію у = f(x) + g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки а) Похідна різниці дорівнює різниці похідних. Нехай у(х) = f(x) - g(x), тоді f(x) = y(x) + g(x) і f'(x) = у`(х) + g'(x), звідси у`(х) = f '(x) - g'(x). б) Похідна суми декількох функцій дорівнює сумі похідних цих функцій, тобто
Приклад. Знайдіть похідні функцій
2) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х, то їхній добуток також — диференційована функція в цій точці і (f(x) • g(x))' = f ' (x) • g(x) + f(x) • g'(x), або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції. Доведення: Розглянемо функцію у = f(x)g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки | а) Постійний множник можна винести за знак похідної:
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
Приклад. Знайдіть похідні функцій:
3) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і
Доведення: Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Похідна елементарних функції:
Наслідки а) Похідна різниці дорівнює різниці похідних. Нехай у(х) = f(x) - g(x), тоді f(x) = y(x) + g(x) і f'(x) = у`(х) + g'(x), звідси у`(х) = f '(x) - g'(x). б) Похідна суми декількох функцій дорівнює сумі похідних цих функцій, тобто
Приклад. Знайдіть похідні функцій
2) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х, то їхній добуток також — диференційована функція в цій точці і (f(x) • g(x))' = f ' (x) • g(x) + f(x) • g'(x), або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції. Доведення: Розглянемо функцію у = f(x)g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки | а) Постійний множник можна винести за знак похідної:
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
Приклад. Знайдіть похідні функцій:
3) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і
Доведення: Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Наслідки а) Похідна різниці дорівнює різниці похідних. Нехай у(х) = f(x) - g(x), тоді f(x) = y(x) + g(x) і f'(x) = у`(х) + g'(x), звідси у`(х) = f '(x) - g'(x). б) Похідна суми декількох функцій дорівнює сумі похідних цих функцій, тобто
Приклад. Знайдіть похідні функцій
2) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х, то їхній добуток також — диференційована функція в цій точці і (f(x) • g(x))' = f ' (x) • g(x) + f(x) • g'(x), або коротко говорять: похідна добутку двох функцій дорівнює сумі добутків кожної функції на похідну другої функції. Доведення: Розглянемо функцію у = f(x)g(x). Зафіксуємо х і надамо аргументу приросту
Наслідки | а) Постійний множник можна винести за знак похідної:
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
Приклад. Знайдіть похідні функцій:
3) Теорема. Якщо функції f(x) і g(x) диференційовані в точці х і
Доведення: Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Числова функція. Область визначення і множина значень функції. Способи завдання функції. Парні і непарні функції. Зростаючі та спадаючі функції. Періодичні функції. Функцією називається залежність змінної у від змінної х, якщо кожному значенню х відповідає єдине значення у. У - залежна змінна (функція) Х - незалежна змінна (аргумент)
Властивості функції 1) областю визначення функції називається множина значень, яких приймає незалежна змінна х
2) областю значення функції називається множина значень, яких приймає залежна змінна у при відповідних значеннях х
Способи задання функції: 1) аналітичний спосіб – полягає у тому, що у виражають через х за допомогою формули. 2) графічний 3) табличний 4) словесний Парні і непарні функції
Зростаючі та спадаючі функції Функцію Функцію Періодичні функції Функція
2. Корінь п-го степеня. Арифметичний корінь п-го степеня, його властивості
3. Степеневі функції, їхні властивості та графіки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

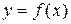


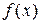 називають зростаючою на множині Р, якщо більшому значенню аргументу з цієї множини відповідає більше значення функції, тобто для будь-яких х1 і х2 з цієї множини з умови х2>х1 випливає, що
називають зростаючою на множині Р, якщо більшому значенню аргументу з цієї множини відповідає більше значення функції, тобто для будь-яких х1 і х2 з цієї множини з умови х2>х1 випливає, що  .
. .
. називається періодичною, якщо існує таке відмінне від нуля число Т щодля любого х з області визначення функції справедливо рівність
називається періодичною, якщо існує таке відмінне від нуля число Т щодля любого х з області визначення функції справедливо рівність 
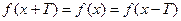 . Число Т називається періодом функції
. Число Т називається періодом функції 

 , де
, де  і
і  , називається показниковою з основою а. (а-стале).
, називається показниковою з основою а. (а-стале).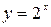

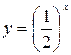




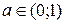






 (на b одиниць вздовж осі ординат)
(на b одиниць вздовж осі ординат)

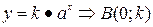
 ) називається показник степеня до якого треба піднести основу а, щоб отримати число b.
) називається показник степеня до якого треба піднести основу а, щоб отримати число b.











 Основна тригонометрична тотожність
Основна тригонометрична тотожність )
)
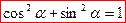


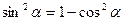
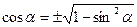







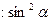




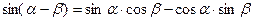







 х. Тоді
х. Тоді
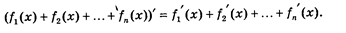







 Нехай у(х)=
Нехай у(х)=  , тоді f(x) = у(х) • g(x). Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, f'(x) = у'(х) • g(x) + у(х) • g'(x). Виразимо з цією формули у'(х):
, тоді f(x) = у(х) • g(x). Знайдемо похідну функції f(x), скориставшись теоремою про похідну добутку, f'(x) = у'(х) • g(x) + у(х) • g'(x). Виразимо з цією формули у'(х):





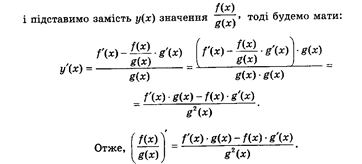 Нехай у(х)=
Нехай у(х)= 


