Операції над функціями. Складена та обернена функція.
Визначимо тепер операції над функціями. Нехай маємо функцію  , яка визначена на множині , яка визначена на множині  , і функцію , і функцію 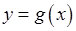 , яка визначена на множині , яка визначена на множині  . Припустимо, що . Припустимо, що  . Тоді на множині . Тоді на множині  можна визначити суму функцій можна визначити суму функцій  . Значення цієї функції у кожній точці . Значення цієї функції у кожній точці  дорівнює сумі дорівнює сумі  . Аналогічно на множині . Аналогічно на множині  можна визначити різницю можна визначити різницю  , добуток , добуток  та частку та частку  цих функцій (останню крім точок, де цих функцій (останню крім точок, де  ). ).
Нехай на множині  визначено функцію визначено функцію  , множиною значень якої є множина , множиною значень якої є множина  . І нехай на множині . І нехай на множині  визначено функцію визначено функцію  , множиною значень якої є множина , множиною значень якої є множина  . Припустимо, що . Припустимо, що  . Тоді на деякій підмножині . Тоді на деякій підмножині  множини множини  визначено так звану складену функцію визначено так звану складену функцію  , множиною значень якої є деяка підмножина , множиною значень якої є деяка підмножина  множини множини  . Тобто складена функція утворюється шляхом підстановки значень одної функції замість аргументу іншої. Така операція називається операцією суперпозиції функцій . Тобто складена функція утворюється шляхом підстановки значень одної функції замість аргументу іншої. Така операція називається операцією суперпозиції функцій 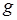 і і  . .
Щоб знайти  – область визначення складеної функції – область визначення складеної функції   , треба з’ясувати, для яких значень , треба з’ясувати, для яких значень  значення функції значення функції  належать області визначення функції належать області визначення функції  . Взагалі кажучи, це досить складна задача. Для її розв’язання, як правило, треба розв’язувати нерівності та системи нерівностей. Значна частина таких нерівностей розглядається у шкільному курсі алгебри. . Взагалі кажучи, це досить складна задача. Для її розв’язання, як правило, треба розв’язувати нерівності та системи нерівностей. Значна частина таких нерівностей розглядається у шкільному курсі алгебри.
Розглянемо приклад. Нехай задано функцію  . Тут . Тут
 . І функцію . І функцію  . Тут . Тут
 . Тоді . Тоді  . .
Утворимо за допомогою суперпозиції функцій  і і 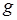 складену функцію: складену функцію:
 . .
Знайдемо її область визначення  . Оскільки . Оскільки 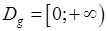 , то повинна виконуватись нерівність , то повинна виконуватись нерівність 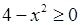 , звідки , звідки  . Тобто . Тобто 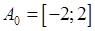 . Множина значень складеної функції: . Множина значень складеної функції:  . .
Введемо тепер поняття оберненої функції. Розглянемо функцію  , яку визначено на деякій множині , яку визначено на деякій множині  , а множиною її значень є множина , а множиною її значень є множина 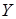 . Припустимо тепер, що для кожного значення . Припустимо тепер, що для кожного значення  існує єдине значення існує єдине значення  таке, що таке, що 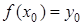 . Тобто двом різним значенням аргументу відповідають різні значення функції. Оскільки у свою чергу згідно з означенням функції . Тобто двом різним значенням аргументу відповідають різні значення функції. Оскільки у свою чергу згідно з означенням функції  існує єдине значення існує єдине значення  таке, що таке, що 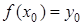 , то між елементами множин , то між елементами множин  та та 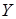 встановлено взаємно однозначну відповідність. Визначимо тепер на множині встановлено взаємно однозначну відповідність. Визначимо тепер на множині 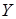 функцію функцію  наступним чином: наступним чином: 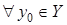 : :  , де , де 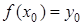 . Тобто фактично кожному значенню функції . Тобто фактично кожному значенню функції  поставлено у відповідність відповідний аргумент цієї функції (він, згідно умови, визначається однозначно). Функція поставлено у відповідність відповідний аргумент цієї функції (він, згідно умови, визначається однозначно). Функція  називається оберненою до функції називається оберненою до функції  . Якщо . Якщо  , то , то  . Зрозуміло, що у свою чергу функція . Зрозуміло, що у свою чергу функція  буде оберненою до функції буде оберненою до функції  . Щоб знайти обернену функцію для функції . Щоб знайти обернену функцію для функції  треба рівняння треба рівняння  розв’язати відносно розв’язати відносно  за умови, що такий розв’язок існує та єдиний. за умови, що такий розв’язок існує та єдиний.
Який вигляд має графік функції, оберненої до даної? Оскільки кожна точка  кривої кривої  є водночас точкою кривої є водночас точкою кривої  , то графік функції , то графік функції  співпадає з графіком функції співпадає з графіком функції  . Тільки якщо у випадку . Тільки якщо у випадку  за відомим значенням за відомим значенням  встановлюється значення встановлюється значення  (рис. 29 а), то у випадку (рис. 29 а), то у випадку  за відомим за відомим  встановлюється значення встановлюється значення  (рис. 29 б). (рис. 29 б).

а б
Рис. 29.
Припустимо тепер, що у виразі  змінні змінні  та та  змінені місцями, тобто розглянемо функцію змінені місцями, тобто розглянемо функцію 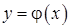 . Тоді кожна точка . Тоді кожна точка  кривої кривої  стане точкою стане точкою  кривої кривої 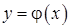 . Оскільки в системі координат . Оскільки в системі координат  точки точки  і і  симетричні відносно прямої симетричні відносно прямої 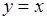 , то графіки взаємно обернених функцій також симетричні відносно цієї прямої, тобто бісектриси 1–го та 3–го координатних кутів (рис. 30). , то графіки взаємно обернених функцій також симетричні відносно цієї прямої, тобто бісектриси 1–го та 3–го координатних кутів (рис. 30).

Рис. 30.
Приклади.
1. Розглянемо функцію 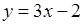 . Тоді звідси: . Тоді звідси:  – обернена до неї. Змінюючи в цій рівності – обернена до неї. Змінюючи в цій рівності  та та  місцями, отримаємо: місцями, отримаємо:  . Зображуємо графіки функцій . Зображуємо графіки функцій 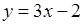 та та  в одній системі координат і переконуємось в тому, що вони симетричні відносно прямої в одній системі координат і переконуємось в тому, що вони симетричні відносно прямої 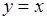 (рис. 31). (рис. 31).

Рис. 31.
2. До функції  оберненою є функція оберненою є функція  (тут вже змінили місцями (тут вже змінили місцями  та та  ). Для цієї функції ). Для цієї функції 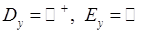 (рис. 32). (рис. 32).

Рис. 32.
3. Побудуємо обернену до функції  . Одразу це зробити неможливо, оскільки, як ми зауважили вище, одному й тому ж значенню функції відповідає безліч значень аргументу (внаслідок періодичності). Тому спочатку ми повинні звузити область визначення цієї функції. Власне розглянути іншу функцію, яку визначено лише на відрізку . Одразу це зробити неможливо, оскільки, як ми зауважили вище, одному й тому ж значенню функції відповідає безліч значень аргументу (внаслідок періодичності). Тому спочатку ми повинні звузити область визначення цієї функції. Власне розглянути іншу функцію, яку визначено лише на відрізку  , і на цьому відрізку її значення співпадають зі значеннями функції , і на цьому відрізку її значення співпадають зі значеннями функції  . Така функція має обернену функцію . Така функція має обернену функцію  . Для неї . Для неї  (рис.33). (рис.33).

Рис. 33.
4. Існують функції, які є оберненими до самих себе. Виникає така ситуація тоді, коли розв’язок рівняння  має вигляд має вигляд  . Наприклад, такими є функції . Наприклад, такими є функції  , ,  . Графіки таких функцій самі симетричні відносно прямої . Графіки таких функцій самі симетричні відносно прямої 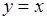 . На рис. 34 зображено графік функції . На рис. 34 зображено графік функції 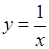 . .

Рис. 34.
Елементарні функції та їх класифікація.
Деякі важливі типи функцій.
Означення. Елементарною функцією називається така функція, яка утворюється з основних елементарних функцій за допомогою скінченного числа операцій додавання, віднімання, множення і ділення, а також операції суперпозиції.
Зауважимо, що тут термін «елементарна» не означає проста. Неелементарні функції можуть бути набагато простішими, ніж елементарні. Наприклад функція
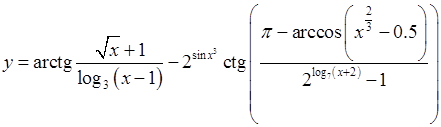 є елементарною (всі потрібні умови виконано). А функція є елементарною (всі потрібні умови виконано). А функція
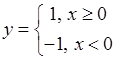 елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції  (нескінченна кількість арифметичних дій), (нескінченна кількість арифметичних дій),  (відповідно ціла і дробова частина (відповідно ціла і дробова частина  ), розглянута вище функція Діріхле та ін. До неелементарних відносяться також так звані спеціальні функції, які відіграють дуже важливу роль у природознавстві. Завдяки фізикам, в математику увійшли й функції більш складної природи – так звані узагальнені функції. ), розглянута вище функція Діріхле та ін. До неелементарних відносяться також так звані спеціальні функції, які відіграють дуже важливу роль у природознавстві. Завдяки фізикам, в математику увійшли й функції більш складної природи – так звані узагальнені функції.
Елементарні функції розділяються на наступні основні класи.
1. Многочлени (або поліноми). Многочленом (поліномом) степеня 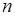 називається функція вигляду: називається функція вигляду:
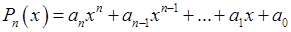 . .
Дійсні числа  називаються коефіцієнтами многочлена. Зокрема, якщо називаються коефіцієнтами многочлена. Зокрема, якщо  , то , то 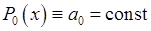 . Якщо . Якщо  , то , то  – лінійна функція. Якщо – лінійна функція. Якщо  , то , то  – квадратний тричлен. – квадратний тричлен.
2. Раціональні функції. Це функції, які є відношенням двох многочленів (не обов’язково однакового степеня):
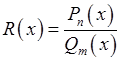 . .
Наприклад:
 . .
Зокрема, многочлени являються частинним випадком раціональних функцій ( ). ).
3. Ірраціональні функції Це функції, які утворюються за допомогою скінченного числа арифметичних дій та операцій суперпозиції з раціональних функцій та степеневих з раціональними показниками. Наприклад:
 . .
Раціональні та ірраціональні функції називаються алгебраїчними. Графіки цих функцій відповідно називаються алгебраїчними кривими. До них, зокрема, відносяться еліпс, гіпербола і парабола.
4. Трансцендентні функції. До цих функцій відносяться ті елементарні функції, які не є алгебраїчними. Це, зокрема, всі тригонометричні та обернені тригонометричні функції, а також показникові та логарифмічні.
Виділимо деякі важливі типи функцій (вони стосуються не лише елементарних функцій), з якими у подальшому нам доведеться мати справу.
1. Обмежені функції.
Означення. Функція  називається обмеженою на множині називається обмеженою на множині  , якщо , якщо  таке, що таке, що  . .
Іншими словами значення обмеженої функції не виходять за межі відрізку  . З геометричної точки зору це означає, що її графік цілком лежить між прямими . З геометричної точки зору це означає, що її графік цілком лежить між прямими  (рис. 35). (рис. 35).

Рис. 35.
Одна й та ж функція на одній множині може бути обмеженою, а на іншій ні. Наприклад, функція  обмежена на відрізку обмежена на відрізку  (на ньому (на ньому  ) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція ) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція  обмежена на відрізку обмежена на відрізку  (тут (тут  ), але не обмежена на півінтервалі ), але не обмежена на півінтервалі 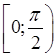 . Функція . Функція  обмежена на всій числовій прямій ( обмежена на всій числовій прямій ( ). ).
2. Монотонні функції.
Означення. Функція  називається зростаючою (спадною) на множині називається зростаючою (спадною) на множині  , якщо , якщо  таких, що таких, що  , виконано нерівність , виконано нерівність  . .
Тобто для зростаючої функції більшому значенню аргументу відповідає і більше значення функції, а для спадної більшому значенню аргументу відповідає менше значення функції.
Означення. Функція  називається неспадною (незростаючою) на множині називається неспадною (незростаючою) на множині  , якщо , якщо  таких, що таких, що  , виконано , виконано  . .
Тобто для неспадної функції більшому значенню аргументу відповідає не менше значення функції, а для незростаючої – більшому значенню аргументу відповідає не більше значення функції.
Схематичні графіки цих функцій зображено на рис. 36 (а – зростаюча, б – спадна, в – неспадна, г – незростаюча).

Рис. 36 (а). Рис. 36 (б).

Рис. 36 (в). Рис. 36 (г).
Одна й та ж функція на одних ділянках числової прямої може бути зростаючою, а на інших спадною. Наприклад, функція  спадна на спадна на 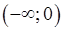 і зростаюча на і зростаюча на  . .
Зростаючі, спадні, неспадні та незростаючі функції поєднуються терміном монотонні функції.
Як відмічалося в п. 16, функція   має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами  та та 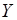 . Таку властивість мають, зокрема, зростаючі та спадні функції. Дійсно, для зростаючої функції з нерівності . Таку властивість мають, зокрема, зростаючі та спадні функції. Дійсно, для зростаючої функції з нерівності  випливає нерівність випливає нерівність  , а для спадної з нерівності , а для спадної з нерівності  випливає нерівність випливає нерівність  . Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція . Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція  зростає (спадає), то обернена функція зростає (спадає), то обернена функція  також зростає (спадає). також зростає (спадає).
3. Парні та непарні функції.
Означення. Функція  називається парною (непарною), якщо називається парною (непарною), якщо  . .
З означення випливає, що область визначення парної чи непарної функції обов’язково симетрична відносно точки  . Графік парної функції симетричний відносно осі . Графік парної функції симетричний відносно осі  (рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)). (рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)).
З основних елементарних функцій парними є, наприклад,  , ,  , ,  , а непарними , а непарними  , ,  , ,  , ,  . .
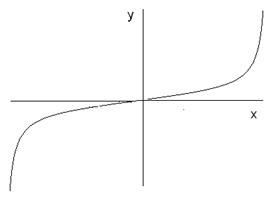 
Рис. 37 (а). Рис. 37 (б).
Не слід думати, що, якщо функція не є парною, то вона непарна. Існує скільки завгодно функцій, які не є ні парними, ні непарними. Наприклад 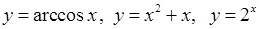 тощо. тощо.
Для побудови графіка парної чи непарної функції достатньо побудувати її графік тільки у правій півплощині, а потім відобразити симетрично відносно осі  (для парної функції), або відносно початку координат (для непарної функції). (для парної функції), або відносно початку координат (для непарної функції).
4. Періодичні функції.
Означення. Функція  називається періодичною, якщо існує таке називається періодичною, якщо існує таке  , що , що  виконано: виконано:  . .
Число 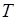 називається періодом функції. Очевидно, що періодом буде також будь яке число виду називається періодом функції. Очевидно, що періодом буде також будь яке число виду  . Найменший з додатних періодів називається основним періодом функції. . Найменший з додатних періодів називається основним періодом функції.
З основних елементарних функцій періодичними являються тригонометричні функції. Основний період функцій  дорівнює дорівнює 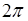 , а функцій , а функцій  дорівнює дорівнює  . .
Для побудови графіка функції, періодичної з періодом 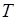 , достатньо побудувати його на будь якому проміжку довжини , достатньо побудувати його на будь якому проміжку довжини 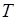 (наприклад, (наприклад,  ), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини ), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини 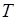 . Якщо, крім того, функція парна, чи непарна, то достатньо побудувати її графік на відрізку . Якщо, крім того, функція парна, чи непарна, то достатньо побудувати її графік на відрізку  . .
18.Границя функції у точці та у нескінченності.
Однобічні границі.
Спробуємо тепер означення границі послідовності, яке було дано у п.9, узагальнити на випадок функції  . Візьмемо деяку послідовність . Візьмемо деяку послідовність  значень аргументу значень аргументу  , яка збігається до числа , яка збігається до числа  , тобто , тобто  . Тоді відповідно значення функції . Тоді відповідно значення функції  також будуть утворювати деяку послідовність також будуть утворювати деяку послідовність 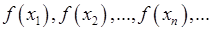
Означення. Число  називається границею функції називається границею функції  при при  (або у точці (або у точці  ), якщо для будь якої послідовності ), якщо для будь якої послідовності 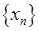 значень аргументу значень аргументу  , такої, що , такої, що  , і , і  , відповідна послідовність значень функції , відповідна послідовність значень функції  збігається до числа збігається до числа  , тобто , тобто  . .
У цьому випадку ми пишемо:
 . .
Наведене означення називається означенням функції на мові послідовностей, або означенням Гейне. *
Існує ще одне означення границі функції, яке полягає у наступному. В п.8 ми інтуїтивно ввели поняття границі функції, як деякого числа  , до якого «наближаються» (або, як кажуть у математиці, прямують) значення функції , до якого «наближаються» (або, як кажуть у математиці, прямують) значення функції  , якщо значення аргументу , якщо значення аргументу  «наближаються» (прямують) до числа «наближаються» (прямують) до числа  . Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргументу . Оскільки у нас з’явилися терміни «наближаються», «близько», треба ввести деяку міру цієї близькості, а саме міру близькості аргументу  до числа до числа  і значення функції і значення функції  до числа до числа  . Позначимо першу з цих мір як . Позначимо першу з цих мір як  . Це буде означати, що . Це буде означати, що
 , (18.1) тобто значення аргументу , (18.1) тобто значення аргументу  потрапляють в потрапляють в  -окіл точки -окіл точки  . Другу з цих мір позначимо як . Другу з цих мір позначимо як 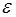 . Це буде означати, що . Це буде означати, що
 , (18.2) тобто значення функції , (18.2) тобто значення функції  потрапляють в потрапляють в 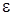 -окіл точки -окіл точки  . За рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості . За рахунок чого може здійснитися друга нерівність? Очевидно, за рахунок достатнього ступеня близькості  до до  , і цей ступінь близькості, очевидно, повинен залежати від , і цей ступінь близькості, очевидно, повинен залежати від 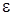 . Іншими словами за заданим числом . Іншими словами за заданим числом  ми повинні знайти число ми повинні знайти число  , яке залежить від , яке залежить від 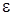 , таке, що виконання нерівності (18.1) забезпечує і виконання нерівності (18.2). Саме цей факт виражає наступне означення. , таке, що виконання нерівності (18.1) забезпечує і виконання нерівності (18.2). Саме цей факт виражає наступне означення.
Означення. Число  називається границею функції називається границею функції  при при  (або у точці (або у точці  ), якщо для кожного додатного числа ), якщо для кожного додатного числа 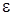 існує таке додатне число існує таке додатне число  , яке залежить від , яке залежить від 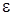 , що для будь яких значень , що для будь яких значень  , що задовольняють нерівність , що задовольняють нерівність  , а також , а також 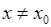 , виконано нерівність , виконано нерівність  . .
У цьому випадку пишемо:  . .
У символьній формі запису це означення має такий вигляд:
  . .
Саме таку форму ми будемо використовувати у подальшому.
Наведене означення називається означенням границі функції на мові « », або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу », або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу  належать множині належать множині 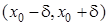 , тобто , тобто 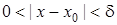 , то значення функції , то значення функції  належать проміжку належать проміжку  , тобто , тобто  . .

Рис. 38.
Теорема. Означення границі функції за Гейне та за Коші еквівалентні.
Доведення. Нехай  у сенсі Коші. Тоді у сенсі Коші. Тоді    . Оберемо довільне . Оберемо довільне  і розглянемо довільну послідовність і розглянемо довільну послідовність 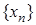 значень аргументу значень аргументу  таку, що таку, що  . Тоді для цього . Тоді для цього  знайдеться номер знайдеться номер  такий, що такий, що  виконано виконано 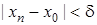 . А тоді . А тоді  . Таким чином вийшло, що . Таким чином вийшло, що   виконано: виконано:  . Це означає, що . Це означає, що  , тобто , тобто  в сенсі Гейне. в сенсі Гейне.
Нехай тепер  в сенсі Гейне. Покажемо, що число в сенсі Гейне. Покажемо, що число  є границею функції є границею функції  в сенсі Коші. Припустимо, що це не так. Тоді в сенсі Коші. Припустимо, що це не так. Тоді 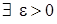  : : 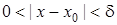  . Побудуємо послідовність . Побудуємо послідовність 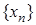 значень аргументу значень аргументу  таку, що таку, що  . Тоді . Тоді  , тобто: , тобто:
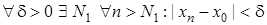 , ,
 . .
В той же час:
 : : 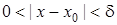  . .
Якщо у якості  взяти взяти  , то отримуємо протиріччя. Отже , то отримуємо протиріччя. Отже  в сенсі Коші. в сенсі Коші.
Теорему доведено.
Приклади.
1. Доведемо, що  . Використаємо означення Коші. Задамо довільне . Використаємо означення Коші. Задамо довільне  і розглянемо: і розглянемо:

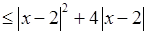 . .
Нехай тепер  . Тоді . Тоді  . Вимагатимемо, щоб останній вираз був менше, ніж . Вимагатимемо, щоб останній вираз був менше, ніж 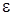 (тоді (тоді  тим більш буде менше, ніж тим більш буде менше, ніж 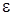 ), тобто ), тобто  . Розв’язком цієї квадратної нерівності (враховуючи, що . Розв’язком цієї квадратної нерівності (враховуючи, що  ) є інтервал ) є інтервал  . Таким чином, якщо ми оберемо . Таким чином, якщо ми оберемо 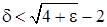 (тобто за заданим (тобто за заданим 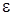 знайшли знайшли  ), то забезпечимо виконання нерівності ), то забезпечимо виконання нерівності  . У якості . У якості  можна взяти будь яке число з інтервалу можна взяти будь яке число з інтервалу  , наприклад , наприклад  . .
2. Довести, що  . .
Знову використаємо означення Коші. Задамо довільне  і розглянемо і розглянемо  : :
 . .
Якщо  , то, обираючи , то, обираючи  (наприклад (наприклад  ), забезпечуємо виконання нерівності ), забезпечуємо виконання нерівності  , що й треба було встановити. , що й треба було встановити.
3. Доведемо, що функція 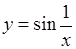 не має ніякої границі при не має ніякої границі при  . Скористаємось тепер означенням Гейне. Розглянемо послідовність . Скористаємось тепер означенням Гейне. Розглянемо послідовність 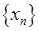 , де , де  . Очевидно, що . Очевидно, що  . В той же час: . В той же час: 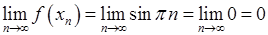 . .
Тепер розглянемо іншу послідовність  , де , де  . Знову . Знову  . Але цього разу . Але цього разу  . .
Отже, для двох різних послідовностей значень аргументу, прямуючих до нуля, відповідні послідовності значень функції мають різні границі – 0 і 1. І тоді, згідно з означенням Гейне, наша функція не має границі при  . .
Вище ми вже відмічали, що не слід змішувати поняття границі функції  у точці у точці  і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було і значення функції у цій точці. Саме тому в означенні границі функції є суттєва умова: треба, щоб було 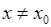 ; або, що те ж саме, ; або, що те ж саме, 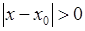 . Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці . Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці  , Але, навіть у тому випадку, коли функція визначена у точці , Але, навіть у тому випадку, коли функція визначена у точці  , її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з п.8. , її границя у цій точці зовсім не обов’язково дорівнює значенню функції у цій точці. Розглянемо детальніше приклад з п.8.

Доведемо, що  . Задамо . Задамо  і розглянемо для будь яких і розглянемо для будь яких  : :
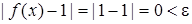 тобто у якості тобто у якості  можна взяти будь яке додатне число. Разом з цим можна взяти будь яке додатне число. Разом з цим  . .
Може бути і така ситуація, коли функція визначена у точці  , а границі функції у цій точці не існує. Розглянемо, наприклад, функцію: , а границі функції у цій точці не існує. Розглянемо, наприклад, функцію:

Ця функція визначена у точці  , а границі у цій точці не існує (див. приклад 3). , а границі у цій точці не існує (див. приклад 3).
В наведених означеннях границі функції значення аргументу  прямувало до скінченого числа прямувало до скінченого числа  . Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид: . Але ці значення можуть прямувати і до нескінченності (саме така ситуація спостерігається, наприклад, тоді, коли у якості функції розглядається послідовність). Тоді означення функції приймає наступний вид:
Означення. Число  називається границею функції називається границею функції  при при  , якщо для будь якого числа , якщо для будь якого числа  існує таке число існує таке число  , що з нерівності , що з нерівності  випливає нерівність випливає нерівність  . .
Тоді пишемо:
 . .
Це означення за змістом близько до означення границі послідовності, тому особливих пояснень не вимагає.
Сама границя функції теж може бути нескінченною.
Означення. Кажуть, що границя функції  при при  дорівнює нескінченності, якщо для будь якого додатного числа дорівнює нескінченності, якщо для будь якого додатного числа 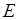 існує таке додатне число існує таке додатне число  , що виконання з нерівності , що виконання з нерівності  випливає нерівність випливає нерівність  . .
Тоді пишемо:  . .
Тобто за рахунок достатньої близькості аргументу  до числа до числа  значення функції значення функції  може бути зроблено за модулем більшим, ніж будь яке наперед задане число може бути зроблено за модулем більшим, ніж будь яке наперед задане число 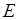 . .
У цьому випадку функція  називається нескінченно великою у точці називається нескінченно великою у точці  . .
Приклад. Довести, що функція  є нескінченно великою у точці є нескінченно великою у точці  . .
Задамо довільне 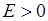 і розглянемо: і розглянемо:
 . .
Якщо  , то , то  | 


 , яка визначена на множині
, яка визначена на множині  , і функцію
, і функцію 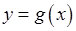 , яка визначена на множині
, яка визначена на множині  . Припустимо, що
. Припустимо, що  . Тоді на множині
. Тоді на множині  можна визначити суму функцій
можна визначити суму функцій  . Значення цієї функції у кожній точці
. Значення цієї функції у кожній точці  дорівнює сумі
дорівнює сумі  . Аналогічно на множині
. Аналогічно на множині  , добуток
, добуток  та частку
та частку  цих функцій (останню крім точок, де
цих функцій (останню крім точок, де  ).
). , множиною значень якої є множина
, множиною значень якої є множина  . Припустимо, що
. Припустимо, що  . Тоді на деякій підмножині
. Тоді на деякій підмножині  множини
множини  , множиною значень якої є деяка підмножина
, множиною значень якої є деяка підмножина  множини
множини 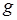 і
і  .
.
 , треба з’ясувати, для яких значень
, треба з’ясувати, для яких значень  значення функції
значення функції  . Тут
. Тут . І функцію
. І функцію  . Тут
. Тут . Тоді
. Тоді  .
. .
. . Оскільки
. Оскільки 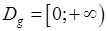 , то повинна виконуватись нерівність
, то повинна виконуватись нерівність 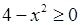 , звідки
, звідки  . Тобто
. Тобто 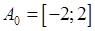 . Множина значень складеної функції:
. Множина значень складеної функції:  .
. , яку визначено на деякій множині
, яку визначено на деякій множині  , а множиною її значень є множина
, а множиною її значень є множина 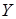 . Припустимо тепер, що для кожного значення
. Припустимо тепер, що для кожного значення  існує єдине значення
існує єдине значення  таке, що
таке, що 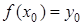 . Тобто двом різним значенням аргументу відповідають різні значення функції. Оскільки у свою чергу згідно з означенням функції
. Тобто двом різним значенням аргументу відповідають різні значення функції. Оскільки у свою чергу згідно з означенням функції  існує єдине значення
існує єдине значення  наступним чином:
наступним чином: 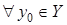 :
:  , де
, де  , то
, то  . Зрозуміло, що у свою чергу функція
. Зрозуміло, що у свою чергу функція  розв’язати відносно
розв’язати відносно  за умови, що такий розв’язок існує та єдиний.
за умови, що такий розв’язок існує та єдиний. кривої
кривої  співпадає з графіком функції
співпадає з графіком функції  встановлюється значення
встановлюється значення  (рис. 29 а), то у випадку
(рис. 29 а), то у випадку 
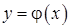 . Тоді кожна точка
. Тоді кожна точка  кривої
кривої  кривої
кривої  точки
точки  і
і  симетричні відносно прямої
симетричні відносно прямої 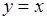 , то графіки взаємно обернених функцій також симетричні відносно цієї прямої, тобто бісектриси 1–го та 3–го координатних кутів (рис. 30).
, то графіки взаємно обернених функцій також симетричні відносно цієї прямої, тобто бісектриси 1–го та 3–го координатних кутів (рис. 30).
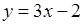 . Тоді звідси:
. Тоді звідси:  – обернена до неї. Змінюючи в цій рівності
– обернена до неї. Змінюючи в цій рівності  . Зображуємо графіки функцій
. Зображуємо графіки функцій 
 оберненою є функція
оберненою є функція  (тут вже змінили місцями
(тут вже змінили місцями 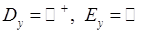 (рис. 32).
(рис. 32).
 . Одразу це зробити неможливо, оскільки, як ми зауважили вище, одному й тому ж значенню функції відповідає безліч значень аргументу (внаслідок періодичності). Тому спочатку ми повинні звузити область визначення цієї функції. Власне розглянути іншу функцію, яку визначено лише на відрізку
. Одразу це зробити неможливо, оскільки, як ми зауважили вище, одному й тому ж значенню функції відповідає безліч значень аргументу (внаслідок періодичності). Тому спочатку ми повинні звузити область визначення цієї функції. Власне розглянути іншу функцію, яку визначено лише на відрізку  , і на цьому відрізку її значення співпадають зі значеннями функції
, і на цьому відрізку її значення співпадають зі значеннями функції  . Для неї
. Для неї  (рис.33).
(рис.33).
 . Наприклад, такими є функції
. Наприклад, такими є функції  ,
,  . Графіки таких функцій самі симетричні відносно прямої
. Графіки таких функцій самі симетричні відносно прямої 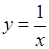 .
.
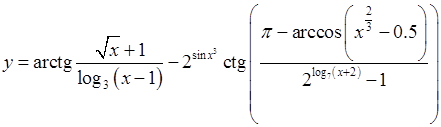 є елементарною (всі потрібні умови виконано). А функція
є елементарною (всі потрібні умови виконано). А функція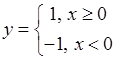 елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції
елементарною не є (вона задається різними виразами на різних інтервалах, а цього не передбачено в означенні елементарної функції). Неелементарними являються також, наприклад, функції  (нескінченна кількість арифметичних дій),
(нескінченна кількість арифметичних дій),  (відповідно ціла і дробова частина
(відповідно ціла і дробова частина 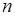 називається функція вигляду:
називається функція вигляду: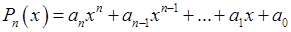 .
. називаються коефіцієнтами многочлена. Зокрема, якщо
називаються коефіцієнтами многочлена. Зокрема, якщо  , то
, то 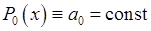 . Якщо
. Якщо  , то
, то  – лінійна функція. Якщо
– лінійна функція. Якщо  , то
, то  – квадратний тричлен.
– квадратний тричлен.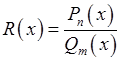 .
. .
. ).
). .
. , якщо
, якщо  таке, що
таке, що  .
. . З геометричної точки зору це означає, що її графік цілком лежить між прямими
. З геометричної точки зору це означає, що її графік цілком лежить між прямими  (рис. 35).
(рис. 35).
 обмежена на відрізку
обмежена на відрізку  (на ньому
(на ньому  ) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція
) і взагалі на будь якому відрізку числової прямої, але не обмежена на всій числовій прямій. Функція  обмежена на відрізку
обмежена на відрізку  (тут
(тут  ), але не обмежена на півінтервалі
), але не обмежена на півінтервалі 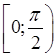 . Функція
. Функція  таких, що
таких, що  , виконано нерівність
, виконано нерівність  .
. .
.

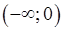 і зростаюча на
і зростаюча на  .
.
 має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами
має обернену тоді і тільки тоді, коли ця функція задає взаємно однозначну відповідність між множинами  . Таку властивість мають, зокрема, зростаючі та спадні функції. Дійсно, для зростаючої функції з нерівності
. Таку властивість мають, зокрема, зростаючі та спадні функції. Дійсно, для зростаючої функції з нерівності  , а для спадної з нерівності
, а для спадної з нерівності  . Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція
. Таким чином, будь яка строго монотонна функція має обернену. При цьому, якщо функція  також зростає (спадає).
також зростає (спадає). .
. . Графік парної функції симетричний відносно осі
. Графік парної функції симетричний відносно осі  (рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)).
(рис. 37 (а)), а непарної – відносно початку координат (рис. 37 (б)). ,
,  , а непарними
, а непарними  ,
,  .
.

 тощо.
тощо. , що
, що  виконано:
виконано:  .
.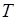 називається періодом функції. Очевидно, що періодом буде також будь яке число виду
називається періодом функції. Очевидно, що періодом буде також будь яке число виду  . Найменший з додатних періодів називається основним періодом функції.
. Найменший з додатних періодів називається основним періодом функції. дорівнює
дорівнює 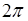 , а функцій
, а функцій  дорівнює
дорівнює  .
. ), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини
), а потім продовжити графік на всю вісь, повторюючи його на кожному проміжку довжини  .
. значень аргументу
значень аргументу  , тобто
, тобто  . Тоді відповідно значення функції
. Тоді відповідно значення функції 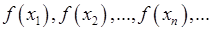
 (або у точці
(або у точці 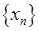 значень аргументу
значень аргументу  , і
, і  збігається до числа
збігається до числа  .
. .
. до числа
до числа  . Це буде означати, що
. Це буде означати, що , (18.1) тобто значення аргументу
, (18.1) тобто значення аргументу 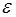 . Це буде означати, що
. Це буде означати, що , (18.2) тобто значення функції
, (18.2) тобто значення функції 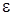 -окіл точки
-окіл точки  ми повинні знайти число
ми повинні знайти число  , яке залежить від
, яке залежить від 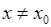 , виконано нерівність
, виконано нерівність  .
.
 .
. », або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу
», або означенням Коші. Геометричну його ілюстрацію наведено на рис. 38. З нього видно, що якщо значення аргументу 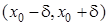 , тобто
, тобто 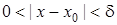 , то значення функції
, то значення функції  , тобто
, тобто 
 у сенсі Коші. Тоді
у сенсі Коші. Тоді 

 і розглянемо довільну послідовність
і розглянемо довільну послідовність 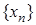 значень аргументу
значень аргументу  . Тоді для цього
. Тоді для цього 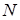 такий, що
такий, що  виконано
виконано 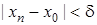 . А тоді
. А тоді  . Таким чином вийшло, що
. Таким чином вийшло, що 
 виконано:
виконано:  , тобто
, тобто  є границею функції
є границею функції 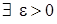
 :
:  . Побудуємо послідовність
. Побудуємо послідовність 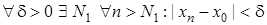 ,
, .
. :
:  , то отримуємо протиріччя. Отже
, то отримуємо протиріччя. Отже  . Використаємо означення Коші. Задамо довільне
. Використаємо означення Коші. Задамо довільне 
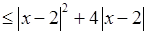 .
. . Тоді
. Тоді  . Вимагатимемо, щоб останній вираз був менше, ніж
. Вимагатимемо, щоб останній вираз був менше, ніж  тим більш буде менше, ніж
тим більш буде менше, ніж  . Розв’язком цієї квадратної нерівності (враховуючи, що
. Розв’язком цієї квадратної нерівності (враховуючи, що  . Таким чином, якщо ми оберемо
. Таким чином, якщо ми оберемо 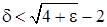 (тобто за заданим
(тобто за заданим  . У якості
. У якості  .
. .
. :
: .
. , то, обираючи
, то, обираючи  (наприклад
(наприклад  ), забезпечуємо виконання нерівності
), забезпечуємо виконання нерівності  , що й треба було встановити.
, що й треба було встановити. не має ніякої границі при
не має ніякої границі при  . Скористаємось тепер означенням Гейне. Розглянемо послідовність
. Скористаємось тепер означенням Гейне. Розглянемо послідовність  . Очевидно, що
. Очевидно, що  . В той же час:
. В той же час: 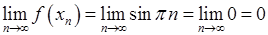 .
. , де
, де  . Знову
. Знову  . Але цього разу
. Але цього разу  .
. . Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці
. Приклад 2 показує, що границя може існувати і тоді, коли функція взагалі не визначена у точці 
 . Задамо
. Задамо  :
: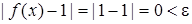 тобто у якості
тобто у якості  .
.
 , якщо для будь якого числа
, якщо для будь якого числа  , що з нерівності
, що з нерівності  випливає нерівність
випливає нерівність  .
. існує таке додатне число
існує таке додатне число  , що виконання з нерівності
, що виконання з нерівності  випливає нерівність
випливає нерівність  .
. .
. є нескінченно великою у точці
є нескінченно великою у точці  .
.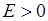 і розглянемо:
і розглянемо: .
.


