
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дві площини збігаються, якщо виконується рівністьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У разі виконання умови (4) рівняння однієї площини можна дістати з рівняння іншої площини множенням на сталий множник. Нехай дано три площини
Вони перетинаються в одній точці у тому і тільки тому разі, коли визначник
Якщо Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл. 3, стор. 87 – 88.
Тема 8 Різні види рівнянь прямої у просторі. Кут між двома прямими у просторі. Умови паралельності і перпендикулярності двох прямих у просторі. Кут між прямою і площиною. Умови паралельності і перпендикулярності прямої і площини
Мета заняття Вивчити різні види рівнянь прямої у просторі, умови || та ┴ двох прямих у просторі, умови || та ┴ прямої та площини, а також формулу для знаходження кута між двома прямими у просторі та кута між прямою та площиною. Розвивати просторове мислення.
Студенти повинні знати: формули обчислення кута між двома прямими у просторі, міх прямою і площиною; умови перпендикулярності та паралельності двох прямих у просторі та між прямою і площиною. Студенти повинні вміти: розв'язувати задачи на формули дляобчислення кутів та умови паралельності і перпендикулярності у просторі. Основні питання теми 1.Параметричні рівняння прямої; 2.Канонічне рівняння прямої; 3.Рівняння прямої, що проходить через 2 дані точки; 4.Пряма, як перетин двох площин; 5.Умови || двох прямих у просторі; 6.Умови ┴ двох прямих у просторі; 7.Умови || прямої і площини; 8.Умови ┴ прямої і площини; 9.Знаходження кута між двома прямими у просторі; 10.Знаходження кута між прямою і площиною;
Завдання для самоперевірки 1.Написати загальні рівняння прямої. Як перейти від загальних рівнянь прямої до канонічних? 2.Як знайти кут між двома прямими в просторі? Написати умови паралельності і перпендикулярності прямих. 3.Через точку М(1;2;3) провести пряму, перпендикулярну до площини, що задана рівнянням 2х – у + 3z + 4 = 0. 4.Через задану точку А(-4;3;1) провести площину, перпендикулярно до прямої, що задана рівнянням (х – 2)/2 = (у – 1)/1 = (z + 1)/3. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор. 90 – 96. Лекція” Різні види рівнянь прямої у просторі” Нехай дано точку М 0(х 0, у 0, z 0) на прямій і вектор За умовою паралельності дістанемо рівняння
яке називається канонічним рівнянням прямої. Пряму можна визначити як результат перетину будь-яких двох площин із наведених далі трьох:
Останні рівняння є рівняннями проекцій прямої відповідно на координатні площини
Якщо дано дві точки М 1(х 1, у 1, z 1), М 2(х 2, у 2, z 2) на прямій, то за напрямний вектор
· З рівняння (2) маємо:
Якщо відомі канонічні рівняння (1), то з них можна вивести параметричні рівняння прямої. Нехай t — коефіцієнт пропорційності векторів З рівнянь
маємо рівняння
Коли параметр t змінюється від – ¥ до + ¥, точка М (х, у, z), де х, у, z визначаються рівнянням (3), пробігає всю пряму. Скориставшись позначеннями
рівняння прямої можна записати у векторній формі
Рівняння прямої у просторі Будь-яка пряма лінія у просторі подається системою двох рівнянь які задають (коли розглядати кожне з них зокрема) дві різні площини, що проходять через цю пряму.
Рівняння (1), узяті разом, називаються загальними рівняннями прямої. Напрямний вектор
Отже, можна вважати що
до канонічного. · Візьмемо Покладемо
Щоб дістати довільну площину, яка проходить через пряму (1), застосовують пучок площин:
Площина і пряма у просторі Будь-яке рівняння першого степеня відносно координат точки простору Кут між двома площинами
Умовою їх паралельності є: Пряма у просторі може бути визначена як перетин двох
або канонічним рівнянням:
де Пряму у просторі можна задати також параметричним рівнянням:
де t — параметр, або рівнянням прямої, що проходить через дві задані точки
Звичайно, всі рівняння відповідають прямій у просторі і між ними існує певний зв’язок. Площина і пряма у просторі можуть перетинатися під деяким кутом a, який визначається за формулою:
У разі виконання умови:
Приклад 1. Скласти рівняння площини, що проходитьчерез вісь ОZ і утворює з площиною Рівняння шуканої площини можна записати у вигляді Приклад 2. Знайти напрямний вектор прямої
і кути, які вона утворює з осями системи координат. Вектори
Тобто: Приклад 3. Показати, що прямі
перетинаються, і написати рівняння площини, в якій вони роз- Дві прямі будуть лежати на одній площині, коли їх напрямні вектори Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор. 90 – 96.
Тема 9 Гіпербола. Парабола. Властивості
Мета заняття Вивчити означення, виведення канонічного рівняння та властивості кривих: гіпербола та парабола. Розвивати логічне мислення.
Студенти повинні знати: означення гіперболи, її рівняння, властивості; означення параболи, її рівняння, властивості. Студенти повинні вміти: розв'язувати задачі, складати різні рівняня гіперболи; розв'язувати задачі, складати різні рівняння параболи; будувати ці криві в системі координат залежно від їх рівняння.
Основні питання теми 1.Означення гіперболи; 2.Розташування в системі координат; 3.Виведення канонічного рівняння; 4.Властивості: осі, вершини, фокуси, асимптоти, ексцентриситет, загальне рівняння, спряжені гіперболи, рівнобічна гіпербола; 5.Означення параболи; 6.Виведення канонічного рівняння параболи; 7.Властивості: вершина, фокус, директриса, вісь симетрії; 8.Розташування параболи в системі координат залежно від її рівняння; 2.5. Криві другого порядку До кривих другого порядку належать: коло, еліпс, гіпербола, парабола. У загальному випадку їм відповідає рівняння:
Шляхом перетворення системи координат із загального рівняння можна одержати канонічні рівняння кривих другого порядку: кола: еліпса: гіперболи: параболи:
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.55 (0.006 с.) |

 . (4)
. (4) . (5)
. (5) .
. , то площини можуть мати спільну пряму, коли система рівнянь (5) має нескінченну множину розв’язків, або не мати жодної спільної точки, коли система (5) не має розв’язків.
, то площини можуть мати спільну пряму, коли система рівнянь (5) має нескінченну множину розв’язків, або не мати жодної спільної точки, коли система (5) не має розв’язків. , паралельний цій прямій. Складемо рівняння прямої. Нехай
, паралельний цій прямій. Складемо рівняння прямої. Нехай 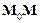 паралельний вектору
паралельний вектору  , який називається напрямним вектором прямої.
, який називається напрямним вектором прямої. , (1)
, (1) .
.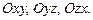
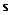 можна взяти
можна взяти  Тоді рівняння прямої набере вигляду
Тоді рівняння прямої набере вигляду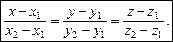 (2)
(2) Складемо рівняння прямої, що проходить через точки М 1(1, 2, 3) і М 2(3, 5, 7).
Складемо рівняння прямої, що проходить через точки М 1(1, 2, 3) і М 2(3, 5, 7). ·
· .
.
 ,
які називаються параметричними рівняннями прямої.
,
які називаються параметричними рівняннями прямої.

 (4)
(4) (1)
(1)

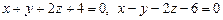
 , та із системи рівнянь
, та із системи рівнянь  ,
,  знайдемо х 1 = 1, у 1 = – 5.
знайдемо х 1 = 1, у 1 = – 5. , то із системи рівнянь
, то із системи рівнянь 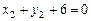 ,
,  знайдемо х 2 = 1, у 2 = – 7. Канонічне рівняння прямої набере вигляду
знайдемо х 2 = 1, у 2 = – 7. Канонічне рівняння прямої набере вигляду . ·
. · . (2)
. (2) відображає площину. Коефіцієнти при змінних А, В, С є компонентами вектора, перпендикулярного до площини.
відображає площину. Коефіцієнти при змінних А, В, С є компонентами вектора, перпендикулярного до площини. і
і 
 визначається за формулою:
визначається за формулою: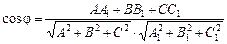 .
. , а перпендикулярності —
, а перпендикулярності —  . Відстань від точки
. Відстань від точки  до площини можна знайти за формулою:
до площини можна знайти за формулою:  .
.
 ,
, — напрямний вектор прямої,
— напрямний вектор прямої,  — точка, що лежить на прямій.
— точка, що лежить на прямій.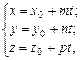
 і
і  :
:

 .
. .
. пряма і площина па-
пряма і площина па- — перпендикулярні. Умовою того, що пряма лежить на площині, є виконання співвідношень:
— перпендикулярні. Умовою того, що пряма лежить на площині, є виконання співвідношень:
 кут 60°, і знаходження її відстані до точки
кут 60°, і знаходження її відстані до точки  .
. , тому що вона проходить через вісь OZ. Використаємо другу умову задачі:
, тому що вона проходить через вісь OZ. Використаємо другу умову задачі: 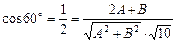 , з якої одержимо рівняння:
, з якої одержимо рівняння:  або
або  . Остаточно маємо, що умовам задачі задовольняють дві площини:
. Остаточно маємо, що умовам задачі задовольняють дві площини: 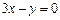 і
і  . Точка А лежить на першій площині, тому що
. Точка А лежить на першій площині, тому що  , а відстань її до другої площини
, а відстань її до другої площини 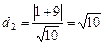 .
.
 і
і  перпендикулярні до відповідних площин, що задають рівняння прямої, тому напрямний вектор прямої
перпендикулярні до відповідних площин, що задають рівняння прямої, тому напрямний вектор прямої  розташований перпендикулярно до кожного з векторів
розташований перпендикулярно до кожного з векторів  . Згідно з означенням векторного добутку векторів
. Згідно з означенням векторного добутку векторів
 або
або  . Кути з осями знайдемо за формулами:
. Кути з осями знайдемо за формулами:  ;
; 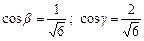 .
. і
і 
 і
і 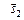 і вектор
і вектор  будуть компланарними. Точка
будуть компланарними. Точка  лежить на першій прямій, а
лежить на першій прямій, а  — на другій. Вектор
— на другій. Вектор 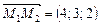 . Напрямний вектор
. Напрямний вектор 
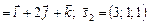 .
.  . Отже, прямі лежать на одній площині. Для запису рівняння цієї площини знайдемо вектор
. Отже, прямі лежать на одній площині. Для запису рівняння цієї площини знайдемо вектор  . Точка
. Точка  лежить на цій площині. Отже, маємо:
лежить на цій площині. Отже, маємо:  або остаточно:
або остаточно:  .
.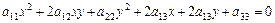 .
. , де
, де 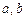 — координати центра кола,
— координати центра кола,  — радіус кола;
— радіус кола; , де
, де  , де а — дійсна, b — уявна півосі гіперболи;
, де а — дійсна, b — уявна півосі гіперболи; , де р — параметр параболи.
, де р — параметр параболи.


