Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умови паралельності i перпендикулярності двох площин.Содержание книги
Поиск на нашем сайте Площини паралельні тоді і тільки тоді, коли
Площини перпендикулярні тоді і тільки тоді, коли Відстань від точки до площини. Щоб знайти відстань від точки до площини треба в ліву частину нормального рівняння підставити координати цієї точки і одержане число за модулем буде відстанню. Якщо d=0, то точка лежить на площині.
24. Пряма у npocтopi. Пряму у просторі будемо розглядати, як лінію перерізу 2 площин або як лінію будь-які точки якої задають вектор коленіарний заданому вектору. Piзні форми рівняння прямоі у npocтopi. Розглянемо різні форми рівнянь прямої у просторі: Загальне р-ня прямої:
Канонічне р-ня прямої: Параметричны р-ня прямої:
Р-ня прямої, що проходить через 2 задані точки: M1(x1, y1, z1) і M2(x2, y2, z2)
Кут між двома прямими у npocтopi. Кут між 2 прямими у просторі – це кут утворений напрямними векторами
Взаємні розташування двох прямих у npocтopi. 1) Лежать в одній площині: Якщо дві прямі лежать в одній площині, то вони або перетинаються, або паралельні.
2) Не лежать в одній площині: Дві прямі, які не лежать в одній площині, називають мимобіжними(Прямі не лежать в одній площині і тому є мимобіжними. Вони не перетинаються, але й не паралельні.).
Якщо площина і пряма, що не лежить у ній, перпендикулярні до однієї і тієї самої прямої, то вони паралельні. Пряма, паралельна деякій прямій, що лежить у площині, паралельна і самій площині. Дві площини, що містять паралельні прямі, перетинаються по прямій, паралельній даним. Площина, що містить деяку пряму, паралельну іншій площині, перетинає останню по прямій, паралельній даній. Якщо одна з двох паралельних прямих паралельна деякій площині, то і інша пряма паралельна цій площині або належить їй. Пряма перпендикулярна до площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині. Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох прямих, що перетинаються і лежать у цій площині. Паралельними є площини, які не мають спільних точок. Якщо ж площини мають спільну пряму, то їх називають перетинними. Дві площини є паралельними, якщо одна з них паралельна двом перетинним прямим, що лежать у іншій площині. Якщо паралельні площини перетинаються третьою, то лінії їх перетину паралельні між собою. Пряма, що лежить в одній із перпендикулярних площин і перпендикулярна до лінії їх перетину, перпендикулярна до іншої площини. Якщо площина перпендикулярна до двох перетинних площин, то вона перпендикулярна до ребра, утвореного ними двогранного кута. Якщо площина перпендикулярна до ребра двогранного кута, то вона перпендикулярна і до площин, що його утворили. Прямі називаються паралельними, якщо вони лежать у одній площині і не мають спільних точок. Кут між паралельними прямими дорівнює 0°. Якщо ж у прямих є спільна точка, то вони називаються перетинними. Кутом між перетинними прямими називається менший із кутів, які утворюються при перетиканні прямих. Якщо прямі не лежать в одній площині і не мають спільних точок, то їх називають мимобіжними. Через кожну з мимобіжних прямих можна провести одну і тільки одну площину, паралельну іншій прямій. Кут між прямою i площиною. Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину. Взаємне розташування прямої i площини. Коло з центром у точці М(a;b) і радіусом R – це геометричне місце точок площини, які віддалені від точки М на відстань R. Канонічне р-ня кола:
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 3491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

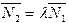 і, отже, A2=lA1, B2=lB1, C2=lC1, або
і, отже, A2=lA1, B2=lB1, C2=lC1, або
 =0 і, отже A1A2+В1B2+C1C2=0
=0 і, отже A1A2+В1B2+C1C2=0

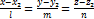

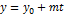
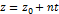
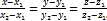
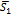 і
і  цих прямих.
цих прямих.

 , а між паралельними прямою та площиною таким, що дорівнює
, а між паралельними прямою та площиною таким, що дорівнює  .
. .
.