
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умови існування подвійного інтеграла та його властавості.Содержание книги
Поиск на нашем сайте
Достатні умови існування подвійного інтеграла. Теорема 1. Якщо функція f (x,y) неперервна у замкненій області Доказ цієї теореми можно провести аналогічно доказу відповідної теореми для визначеного інтеграла. Теорема 2. Якщо функція f (x,y) обмежена у замкненій області Властивості подвійного інтеграла: 1. Подвійний інтеграл 2. Постійний множник k можно виносити за знак подвійного інтеграла: 3. Подвійний інтегралвід сумы двох функцій дорівнює сумі подвійних інтегралів від доданків: 4. Якщо область 5. Якщо в области 6. Якщо в области 7. Якщо функція 8. Дійсно, так як у даному випадку Властивість 8 дозволяє використовувати подвійні інтеграли для знахождення плоских фігур.
61.Обчислення подвійного інтеграла в прямокутних координатах. 1)якщо область D, в якій розглядається подвійний інтеграл, є прямокутником з паралельними координатним осям сторонами, які задано рівняннями x=a, x=b, y=c,y=d(a<=x<=b, c<=y<=d), то подвійний інтеграл обчислюється за однією з формул: 2)Коли область D така, що будь-яка пряма, що проходить усередині цієї області і паралельна осі Oy, перетинає її межу в двох точках, то ця область називається простою відносно осі Ox і визначається системою нерівностей виду a<=x<=b, 3)якщо межа області D перетинається у двох точках будь-якою прямою, що проходить усередині цієї області і паралельна осі Ox, то ця область називається простою відносно осі Oy і визначається системою нерівностей виду c<=y<=d, 4)Якщо нижня та верхня лінії межі області D складаються з кількох частин, що мають різні рівняння, то таку область необхідно розбити прямими, паралельними осі Oy, на частини, щоб кожна з них подавалася одним рівнянням.У цьому разі обчислення подвійного інтеграла зводиться до обчислення двох або більше повторних інтересів.
Диференціальні рівняння 1-го порядку, ix геометрична інтерпритація. Загальний i частинний розв'язки. Задача Koшi. Теорема існування i єднисті розв'язків диференціального рівняння. . Диференціальним рівнянням називають рівняння, яке містить незалежну змінну х, шукану функцію у і її похідні у, у,..., у(N). Порядком диференційного рівняння називаєтьсчя порядок найвищої похідної, яка входить у рівняння. Приклад: ху'+у-2-0 диференціальне рівняння І порядку. З геометричної точки зору проінтегрувати диференціальне рівняння – це знайти криві, дотичні яких збігаються з напрямом поля у відповідних точках. Загальним розв'язком диференціального рівняння першого порядку називається функція 1) вона задовольняє диференціальному рівнянню при довільному конкретному значенню сталої 2) якою б не була початкова умова (із області, в якій виконуються умови теореми існування і єдності розв'язку), можна знайти таке значення, що функція задовольняє даній початковій умові. Частинним розв'язком називається довільна функція яка одержується із загального розв'язку якщо в останньому довільній сталій надати певного значення. Співвідношення називається в цьому випадку частинним інтегралом. Розгл. ДР y’=f(x;y). Задача пошуку розв. у=j(х), що задов. умови у=у0 при х=х0 наз. задачею Коші. Умови наз. початковими, а у0, х0 – поч. знач. Нехай ф-ція f(x;y) непер. на обл. D і задов. в цій обл. умову Ліпшиця:
тоді при (х0, у0)ÎD існує єд. розв. у=j(х) ДР, який задов. поч.. умови у0=j(х0).
Рівняння з відокремлюваними змінними. Диференціальне рівняння вигляду
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.008 с.) |

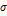 , то подвійний інтеграл існує
, то подвійний інтеграл існує 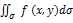 .
. не залежить позначення змінних інтегрування.
не залежить позначення змінних інтегрування.

 разбита на дві області
разбита на дві області  и
и  , то
, то
 то
то
 то
то
 задана в области
задана в области 

 в області
в області  отримуємо:
отримуємо:
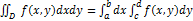


 (x).Тоді для обчислення подвійного інтеграла дістаємо формулу
(x).Тоді для обчислення подвійного інтеграла дістаємо формулу 
 (x).Тоді подвійний інтеграл обчислюється за формулою
(x).Тоді подвійний інтеграл обчислюється за формулою 

 яка залежить тільки від однієї довільної сталої і задовольняє таким умовам:
яка залежить тільки від однієї довільної сталої і задовольняє таким умовам: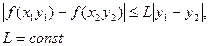
 називається рівнянням з відокремлюваними змінними. Якщо
називається рівнянням з відокремлюваними змінними. Якщо  , то змінні відокремлюються діленням обох частин рівняння на
, то змінні відокремлюються діленням обох частин рівняння на  . Маємо
. Маємо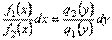 , тобто рівняння, що зводяться до рівнянь з відокремленими змінними.
, тобто рівняння, що зводяться до рівнянь з відокремленими змінними.


