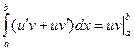Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування ірраціональних i деяких тригонометричних функцій.Содержание книги
Поиск на нашем сайте Розглянемо òR(sinx,cos x)dx, де R – раціональна ф-ія відносно sin, cos, тобто над sin, cos викон. лише арифметичні дії та піднесення до цілого степеня. Існують такі підстановки, що за їх допомогою інтеграл òR(sinx,cosx)dx завжди може бути зведений до інтеграла від раціональної ф-ії òR*(t)dt, загальна схема інтегрування якої розроблена. 1)Універсальна тригонометрична підстановка 2) Підінтегральна ф-ія – непарна відносно sin x, тоді роблять підстановку cos x = t. 3) Підінтегральна ф-ія – непарна відносно cos x раціоналізується за допомогою підстановки sin x = t. 4) Підінтегральна ф-ія R(sin x, cos x) – парна по sinx, cosx сукупно, тобто R(-sinx,-cosx)=R(sinx,cosx). В цьому випадку використовують підстановку tgx=t або ctgx=t. 5) Підінтегральна ф-ія R(tgx) раціоналізується підстановкою tgx=t. В інтегралах òsin2nx×cos2mxdx рекомендується скористатися формулами зниження степеня.
Інтегрування ірраціональних функцій. 1.
2.
3.
Підінтегральна ф-ія
Означення визначеного інтеграла i геометричний зміст. Означення: Якщо існує скінченна границя інтегральних сум Sn при lіà0 і не залежить ні від способу розбиття [a;b] на частини Dхі, ні від вибору точок
Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною. Геометричний зміст: поняття визначеності інтеграла введено таким чином, що в разі, коли ф-ія
Ми можемо вказати значення деяких інтегралів,використовуючи відомі планометричні формули для площей плоских фігур. Наприклад:
Властивості визначеного iнтеграла. Формула Ньютона-Лейбніца. 1) Якщо f(x)=c=const, то 2) Сталий множник можна виносити з-під знака визначеного інтеграла.
3) Якщо f1(x) та f2(x) інтегровні на [a;b], то: 4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.
5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.
6) Якщо f(x) – інтегровна в будь-якому із проміжків [a;b], [a;c], [c;b], то: 7) Якщо f(x)³0 і інтегровна для xÎ[a,b], b>a, то
8) Якщо f(x), g(x) – інтегровні та f(x)³g(x) для xÎ[a;b], b>a, то:
9) Якщо f(x) – інтегровна та m£f(x)£M, для xÎ[a;b], b>a, то 10) (Теорема про середнє): Якщо ф-ія f(x) – неперервна для xÎ[a;b], b>a, то знайдеться така точка x= cÎ [a;b], що: Теорема (Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для xÎ [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:
Таблиця інтегралів.
Заміна змінної і інтегрування частинами у визначеному інтегралі. Метод заміни змінної. При обчисленні визначених інтегралів, як і невизначених, широко користуються методом заміни змінної (або методом підстановки). Теорема 1. Нехай виконуються умови: 1) функція f(x) неперервна на відрізку [а;b]; 2) функція x = 3) Тоді справджується рівність
Оскільки функція f(x) неперервна на [а;b], то вона має первісну. Позначимо її через F(x), x Метод інтегрування частинами Теорема 2. Якщо функції
Оскільки функція uv є первісною функції (uv)' -u'v + uv', то за формулою Ньютона-Лейбніца дістанемо
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |

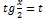 . На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.
. На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.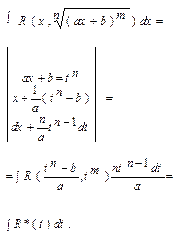

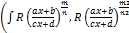
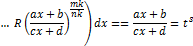
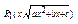 після виділення повного квадрата і заміни
після виділення повного квадрата і заміни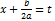 раціоналізується тригонометричними підстановками.
раціоналізується тригонометричними підстановками. і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:
і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається: 54.
54. 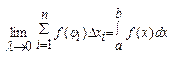 За означенням, визначений інтеграл
За означенням, визначений інтеграл 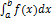 – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.
– число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.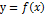 додатня на відрізку [а,b], де а быльше,
додатня на відрізку [а,b], де а быльше, и т.д.
и т.д.
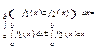


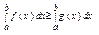

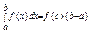

 (t) і її похідна х' =
(t) і її похідна х' =  ;
;  ];
]; (
(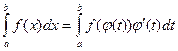 (1)
(1)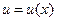 i
i 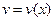 мається на відрізку [а;b] мають неперервні похідні, то справедлива формула
мається на відрізку [а;b] мають неперервні похідні, то справедлива формула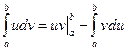 (формула інтегрування частинами визначеного інтеграла.)
(формула інтегрування частинами визначеного інтеграла.)