
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еліпс. Канонічне рівняння та рівняння зi зміщеним центром.Содержание книги
Поиск на нашем сайте Еліпс – геометричне місце точок, для яких сума відстаней від 2 заданих точок(фокусів) – величина стала. Канонічне р-ня еліпса(якщо осі координат збігаються з осями еліпса): Гіпербола. Канонічне рівняння та рівняння зі зміщеним центром. Асимптота гіперболи. Гіпербола – геометричне місце точок, для кожної з яких різниця відстаней від двох заданих точок(фокусів) – величина стала. Канонічне рівняння (якщо вісь Ох збігається з дійсною віссю гіперболи):
Парабола – геометр.місце точок M(x, y), рівновіддалених від даної точки(фокуса) і від даної прямої(директриси).Канонічне р-ня параболи: Основні властивості функції. Функцією у = f(x) називається така відповідність між множинами D і Е, при якій кожному значенню змінної х відповідає одне й тільки одне значення змінної у. Розрізняють три способи завдання функції: аналітичний, графічний і табличний. Щоб задати функцію, потрібно вказати спосіб, за допомогою якого для кожного значення аргументу можна знайти відповідне значення функції. Найбільш уживаним є спосіб завдання функції за допомогою формули у=f(x), де f(x)-вираз, що містить змінну х. У такому випадку говорять, що функція задана формулою або що функція задана аналітично. Властивості: 1. Функція називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції: Х[ > х2 ^ f(xl) > f(x2); Xj; х2 є D. 2. Функція називається спадною, якщо меншому значенню аргументу відповідає більше значення функції Xj < х2 ^ /(xj > f(x2); х1;х1 є D. 3. Функція називається монотонною, якщо вона лише зростаюча або лише спадна в своїй області визначення. 4. Функція називається парною, якщо зміна знаку аргументу не викликає зміни знаку функції f(-x) = f(x), x; -x є D. 5. Функція називається непарною, якщо зміна знаку аргументу викликає лише зміни знаку функції f(—x) - -f(x), х; - х е D. 6. Функція називається обмеженою зверху, якщо для неї існує таке число М, що виконується умова f(x) < М, х <=D. Функція називається обмеженою знизу, якщо для неї існує таке число т, що виконується умова f(x) >т, х <=D. 8. Функція називається обмеженою, якщо вона обмежена знизу і зверху т < f(x) < М, х <=D. 9. Фунція називається періодичною, якщо існує таке число Т, для якого виконується умова fix — Т) - f(x) - fix + Т), х е D. Обернена i складна функція однієї змінноі. Приклади. Якщо ф-я Будь-який впорядкований (занумерований) дискретний набір чисел називають числовою послідовністю: Число А називається границею числової послідовності { Границя функції. Число А називають границею функції y=f(x), тобто При цьому кажуть, що функція “прямує” до А за умови, що її аргументи х наближаються все ближче до х0. Важливо, що сама функція в точці х0 може бути і не заданою. Число В називають границею функції y=f(x), коли Розглянемо односторонні границі для функції Правостороння границя функції:
Лівостороння границя функції:
Якщо Сталу можна виносити за знак границі: Ознаки існування границі. Для існування
Функція у=f(х) називається нескінченно малою в точці х0, якщо Функція у=f(х) називається нескінченно великою в точці х0, якщо Нехай функції у1(х) та у2(х) – безмежно малі в деякій точці х0. Тоді у1(х) називають нескінченно малою більш високого порядку, ніж у2(х) в точці х0, якщо Нехай функції у1(х) та у2(х) – безмежно малі в деякій точці х0. Тоді у1(х) та у2(х) називають еквівалентно малими в точці х0, якщо Властивості неск. мал.: 1) Алгебраїчна сума скінченого числа неск. мал.. величин є неск. мал.. величиною. 2) Добуток неск. мал.. величин на обмежену ф-ю(в тому числі на константу і на інші неск. мал.. ф-ї) є величиною неск. малою. 3) Частка від ділення неск. мал.. величин на ф=ю границі якої відміна від 0 є неск. мал.. величина. Властивості неск. вел. величин: 1) f(x) неск. вел. Величина, т. 2) f(x), φ(x) - неск. вел. Величини, f(x)+φ(x) - неск. вел. Величини 3) частка від ділення неск. вел. Величин
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

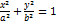
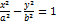 . Асимптотою назив. Пряма така, що точка, яка віддаляється в нескінченність необмежено наближується до даної прямої. Гіпербола має 2 асимптоти:
. Асимптотою назив. Пряма така, що точка, яка віддаляється в нескінченність необмежено наближується до даної прямої. Гіпербола має 2 асимптоти:  ;
;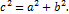
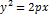
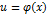 визначена на області D, G – область її значень, ф-я
визначена на області D, G – область її значень, ф-я  визначена на області G, то ф-я
визначена на області G, то ф-я  називається складною функцією, яка складна із ф-й
називається складною функцією, яка складна із ф-й 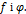
 ,
,  , тобто послідовність – функція натурального аргументу.
, тобто послідовність – функція натурального аргументу.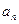 }, пишуть
}, пишуть 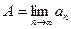 , якщо для будь-якого ε>0 знайдеться таке натуральне N, що для всіх n>N виконається умова
, якщо для будь-якого ε>0 знайдеться таке натуральне N, що для всіх n>N виконається умова 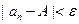 . Геометрично це означає, що всі наступні після
. Геометрично це означає, що всі наступні після 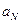 елементи послідовності з номерами
елементи послідовності з номерами 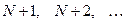 обов′язково попадуть в ε -окіл точки А числової прямої
обов′язково попадуть в ε -окіл точки А числової прямої , якщо для будь-якого ε>0 знайдеться таке δ>0, що як тільки її аргументи х попадають у δ -окіл точки х0, так одразу відповідні у=f(x) попадають в ε -окіл точки А. Іншими словами, при виконанні умови
, якщо для будь-якого ε>0 знайдеться таке δ>0, що як тільки її аргументи х попадають у δ -окіл точки х0, так одразу відповідні у=f(x) попадають в ε -окіл точки А. Іншими словами, при виконанні умови  обов′язково виконується нерівність
обов′язково виконується нерівність  .
. , тобто
, тобто  , якщо для будь-якого ε>0 існує число
, якщо для будь-якого ε>0 існує число 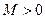 таке, що з нерівності
таке, що з нерівності 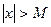 випливає нерівність
випливає нерівність  .
. , тобто коли
, тобто коли  з одного певного боку. При цьому домовимось, що позначення
з одного певного боку. При цьому домовимось, що позначення  означає наближення зліва, а позначення
означає наближення зліва, а позначення  - відповідно справа.
- відповідно справа. .
.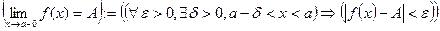 .
.  ,
,  , то
, то  ;
;  ;
;  . В останньому випадку має виконуватись умова В
. В останньому випадку має виконуватись умова В  0.
0.
 необхідно і достатньо, щоб виконувалась умова
необхідно і достатньо, щоб виконувалась умова 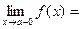
 .
. .
.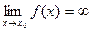 .
. . Відповідно у1(х) називають нескінченно малою більш низького порядку, ніж у2(х) в точці х0, якщо
. Відповідно у1(х) називають нескінченно малою більш низького порядку, ніж у2(х) в точці х0, якщо  .
. .
.
 , f(x) і g(x) - неск. вел. Величини.
, f(x) і g(x) - неск. вел. Величини. є величиною неск. великою.
є величиною неск. великою.


