
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частинні похідні.Повний диференціал.Частинні похідні та диференціали pізних порядків.Содержание книги
Поиск на нашем сайте
Озн. Частинною похідною від ф-ції z=f(x;у) на змінній х називається границя відношення частинного приросту ф-ції до приросту змінної х, коли останній прямує до 0. Аналогічно і по змінній у. Для знаходження частинної похідної Отже, за озн. Частинними похідними 2-го порядку від ф-ції z=f(x,y)називаються частинні похідні від похідних першого порядку.
Озн. Диференціалом функції називається сума добутків частинних похідних цієї функції на приріст відповідних незалежних змінних, тобто: Визначення. Функція z = f(x,у) називається диференційованою в точці (х, у), якщо її повний приріст може бути представлено у вигляді 46. Похідна від складної функції багатьох змінних. Похідна від заданої неявно функції. Похідна складної функції дорівнює добутку похідної зовнішньої функції за проміжним аргументом на похідну проміжного аргументу за незалежною змінною. (f(g(x)))' = f'(g(x))•g'(x). Похідна неявної ф-ії: Якщо існує неперервна ф-ія однієї змінної y=f(x) така, що відповідні пари (x;y) задовольняють умову F(x;y), тоді ця умова називається неявною формою ф-ії f(x), сама ф-ія f(x) називається неявною ф-ією, яка задовольняє умову F(x;y)=0. Припустимо,що неперервна ф-ія y=f(x) задана в неявній формі F(x;y)=0 і що
Аналогічно частинні похідні ф-ії двох незалежних змінних z=f(x;y), яка задана за допомогою рівняння F(x;y;z)=0 де F(x;y;z) – диференційовна ф-ія змінних x,y,z, можуть бути обчислені за формулами: за умови, що 47. Похідна за напрямом. Градієнт функції. Означення: Нехай ф-ія z=f(x;y) визначесна в деякому околі точки P0=(x0;y0); l деякий промінь з початком в точці P0=(x0;y0); P=(x;y) – точка на цьому промені, яка належить околу, що розглядається, – околу точки P0=(x0;y0); Dl – довжина відрізка P0Р. Границя В частинному випадку, Похідна за напрямом Градієнтом
За формулою довж вектора знаходять величину цієї найбільшої швидкості:
48.Екстремум функції багатьох змінних. Необхідна i достатня умови екстремуму. Означення: Нехай ф-ія z=f(x;y) визначена в деякому околі точки (x0;y0) і неперервна в цій точці. Якщо для всіх точок (x;y) цього околу виконується нерівність Точки максимуму і мінімуму наз. точками екстремуму. В т. екстремуму ф-ції її частинна похідна = 0 або не існує Þ в т. екстремуму диференційованої ф-ції виконується нерівність: df/dx=0 і df/dy=0. Необхідна:
Достатня:
AC – B2<0 – НЕ ІСНУЄ АС – В2=0 –? A=¶2z/¶x2 (M0) C=¶2z/¶y2 (M0) B=¶2z/¶x¶y (M0) Дослідження функції двох змінних на екстремум рекомендується проводити за такою схемою: 1. Знайти частинні похідні функції 2. Вирішити систему рівнянь 3. Знайти частинні похідні другого порядку(аналогічно і вищих порядків), обчислити їх значення в кожній критичній точці і за допомогою достатньої умови зробити висновок про наявність екстремумів. 4. Знайти екстремуми (екстремальні значення) функції.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.208.127 (0.006 с.) |

 (x,y) треба вважати сталою змінну у, а для
(x,y) треба вважати сталою змінну у, а для  (x,y)-змінну х. Позначається частинна похідна так:
(x,y)-змінну х. Позначається частинна похідна так: 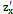 ;
;  ;
;  або
або 
 =
= 
 ;
;  .
. ;
;  ;
;  ;
;  . Аналогічно визначаються частинні похідні 3-го, 4-го і т. д. порядків.Так
. Аналогічно визначаються частинні похідні 3-го, 4-го і т. д. порядків.Так  ,
, 

 ,де
,де  -диференціал ф-ції,
-диференціал ф-ції,  ,
, 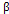 -нескінченно малі при
-нескінченно малі при  Таким чином, диференціал функції декількох змінних, як і у випадку однієї змінної, представляє головну, лінійну щодо приросту
Таким чином, диференціал функції декількох змінних, як і у випадку однієї змінної, представляє головну, лінійну щодо приросту  х і
х і  . Похідна
. Похідна  знаходиться за формулою:
знаходиться за формулою:

 .
.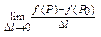 , якщо вона існує, називається похідною ф-ії z=f(x;y) за напрямом
, якщо вона існує, називається похідною ф-ії z=f(x;y) за напрямом  в точці Р0 і позначається
в точці Р0 і позначається 
 є похідна ф-ії z=f(x;y) за доданим напрямом осі Ох, а
є похідна ф-ії z=f(x;y) за доданим напрямом осі Ох, а  – за напрямом осі Оу.
– за напрямом осі Оу. характеризує швидкість зміни ф-ії z=f(x;y) в точці P0=(x0;y0) за напрямом
характеризує швидкість зміни ф-ії z=f(x;y) в точці P0=(x0;y0) за напрямом  вектор з координатами (
вектор з координатами ( ). Похідна за напрямом є скалярним добутком градієнта
). Похідна за напрямом є скалярним добутком градієнта  і одиничного вектора, задающого напрям l. Градієнта
і одиничного вектора, задающого напрям l. Градієнта 


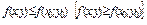 , тоді ця точка (x0;y0) називається точкою максимуму (мінімуму) ф-ії z=f(x;y).
, тоді ця точка (x0;y0) називається точкою максимуму (мінімуму) ф-ії z=f(x;y).


 ,
,  і знайти критичні точки функції.
і знайти критичні точки функції.


