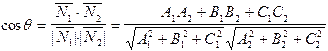Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скалярний добуток векторів, його властивості. Вираз скалярного добутку через координати векторів.Содержание книги
Поиск на нашем сайте
Скалярним добутком векторів
Скалярний добуток векторів – число, що дорівнює добутку довжини одного з векторів на проекцію 2-го взятого напрямку.
Геометричні властивості:
11. Векторний добуток векторів, його властивості. Координати векторного добутку двох векторів. Добутком вектора
Властивості:
12.Мішаним добутком векторів Властивості мішаного добутку: 1).( 13. Вектор Вектори 14. Базисом на прямій називається будь-який ненульовий вектор
15. Проекцією вектора на вісь називається різниця координат кінця та початку вектора. Теорема. Проекція вектора на вісь u дорівнює добутку довжини цього вектора на cos кута його нахилу до осі ( 16. Декартовою системою координат і на прямій, і на площині, і в просторі називається сукупність точки О(початок координат) і базису. Декартовими координатами точки називають координати її радіус-вектора якщо базисні вектори декартової системи координат мають різну довжину і кути між ними не всі прямі, то така система координат загальнодекартова. Якщо базисні вектори декартової системи координат є ортами і кути між ними не всі прямі, то така система називається косоугольною. Якщо базисні вектори декартової системи координат одиничні і взаємно перпендикулярні, то декартова система координат називається прямокутною. Її базис називається ортонормованим, координати вектора і точки називаються прямокутними. Теорема про геометричний зміст декартових прямокутних координат вектора. Декартові прямокутні координати вектора дорівнюють проекціям цього вектора на координати осі(ox,oy,oz). 17. Розглянемо рівняння першого ступеня з двома змінними у загальному вигляді 18. Канонічне рівняння прямої – це рівняння прямої Ɩ, яка проходить через точку Якщо в (1.1) відношення позначити літерою t, то можна виразити x,y,z через t, тобто записати рівняння прямої в параметричній формі Рівняння прямої, яке проходить через дві задані точки 19. Рівняння прямої у відрізках. Знайдемо рівняння прямої по заданим відрізкам, які відсікаються на осях координат. Використовуючи Рівняння прямої з кутовим коефіцієнтом. Нехай пряма перетинає вісь Oy в точці B(0;b) і утворює з віссю Ox кут α. Візьмемо на прямій довільну точку M(x;y). Тоді знайдемо тангенс кута α нахилу прямої з прямокутного трикутника MBN: 20. Відстань від точки до прямої. Відстань від точки 21.Кут між прямими Нехай дано дві прямі
22.Площина – алгебраїчна поверхня першого порядку. Основні типи рівнянь площин. Загальне (повне) рівняння площини: (1.1); рівняння площини у відрізках:
Кут між двома площинами. Кутом між двома площинами називають один із суміжних двогранних кутів або, утворених цими площинами. Якщо площини не перетинаються, тобто паралельні, то кут між ними дорівнює 0. Тепер розглянемо задачу про обчислення кута між двома площинами. Кут між двома площинами, точніше один із суміжних кутів між двома площинами, може бути обчислений як кут між нормалями до цих площин. Якщо площини задані своїми загальними рівняннями: A1x+B1y+C1z+D1=0 A2x+B2y+C2z+D2=0, тоді їх нормальні вектори мають вигляд
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 940; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.91.15 (0.006 с.) |

 наз. число, що дорівнює добутку довжини цих векторів на cos кута між ними.
наз. число, що дорівнює добутку довжини цих векторів на cos кута між ними.
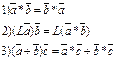

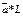 наз.
наз. 




 називається число (
називається число ( Вектори
Вектори  . Модуль
. Модуль  дорівнює об'єму паралелепіпеда, побудованого на векторах. Нехай
дорівнює об'єму паралелепіпеда, побудованого на векторах. Нехай  =
=  . Висота паралелепіпеда дорівнює
. Висота паралелепіпеда дорівнює  . Якщо відомі проекції векторів
. Якщо відомі проекції векторів 

 то мішаний добуток обчислюється за формулою: (
то мішаний добуток обчислюється за формулою: ( =
= 
 . 2).(
. 2).( =0 тоді і тільки тоді, коли вектори
=0 тоді і тільки тоді, коли вектори 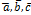

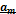 називається лінійною комбінацією векторів
називається лінійною комбінацією векторів  векторного простору R, якщо він дорівнює сумі добутку цих векторів на довільні дійсні числа:
векторного простору R, якщо він дорівнює сумі добутку цих векторів на довільні дійсні числа:  де
де  довільні числа.
довільні числа. , які не дорівнюють нуль, що
, які не дорівнюють нуль, що  =0 В протилежному випадку вектори
=0 В протилежному випадку вектори  називаються лінійно незалежними. Відзначимо деякі властивості векторів лінійного простору: 1).Якщо серед векторів
називаються лінійно незалежними. Відзначимо деякі властивості векторів лінійного простору: 1).Якщо серед векторів  на цій прямій. Цей вектор
на цій прямій. Цей вектор  називається базисним. Нехай на прямій Ɩ задано базис
називається базисним. Нехай на прямій Ɩ задано базис  . Для будь-якого вектора
. Для будь-якого вектора  колінеарного даній прямій, визначено ставлення
колінеарного даній прямій, визначено ставлення  , причому число x визначається однозначно. Таким чином, справедлива наступна теорема. Теорема 1.1 (про розкладання вектора по базису на прямій). Будь-який вектор а, колінеарний прямий, може бути розкладений за базисом на цій прямій, тобто представлений у вигляді
, причому число x визначається однозначно. Таким чином, справедлива наступна теорема. Теорема 1.1 (про розкладання вектора по базису на прямій). Будь-який вектор а, колінеарний прямий, може бути розкладений за базисом на цій прямій, тобто представлений у вигляді  (1.1),де число x визначається однозначно.
(1.1),де число x визначається однозначно. . Оскільки вектори
. Оскільки вектори  колінеарні, то і координата x однозначно визначається їх відношенням x=
колінеарні, то і координата x однозначно визначається їх відношенням x=  . Наприклад, якщо вектор
. Наприклад, якщо вектор  представляється у вигляді
представляється у вигляді  то x =- 2 - його координата щодо базису
то x =- 2 - його координата щодо базису 
 на цій площині, взяті в певному порядку. Ці вектори
на цій площині, взяті в певному порядку. Ці вектори  .Має місце наступна теорема. Теорема 1.2 (про розкладання вектора по базису на площині). Будь-який вектор
.Має місце наступна теорема. Теорема 1.2 (про розкладання вектора по базису на площині). Будь-який вектор  на цій площині, тобто представлений у вигляді (1.2), де числа
на цій площині, тобто представлений у вигляді (1.2), де числа  визначаються однозначно. Коефіцієнти
визначаються однозначно. Коефіцієнти  і
і  в розкладанні (1.2) називаються координатами вектора а щодо базису. Базисом в просторі називаються три некомпланарних вектора
в розкладанні (1.2) називаються координатами вектора а щодо базису. Базисом в просторі називаються три некомпланарних вектора  взяті в певному порядку. Ці вектори
взяті в певному порядку. Ці вектори  +
+  (1.3) Має місце наступна теорема. Теорема 1.3 (про розкладання вектора по базису в просторі). Будь-який вектор
(1.3) Має місце наступна теорема. Теорема 1.3 (про розкладання вектора по базису в просторі). Будь-який вектор  визначаються однозначно. Коефіцієнти
визначаються однозначно. Коефіцієнти  .
. =
=  ). Лінійні властивості проекції вектора на вісь. 1). При додаванні(відніманні) векторів їх проекції на довільну вісь додаються(віднімаються). Тобто,
). Лінійні властивості проекції вектора на вісь. 1). При додаванні(відніманні) векторів їх проекції на довільну вісь додаються(віднімаються). Тобто,  2).При множенні вектора на число його проекція на довільну вісь множиться на це число. Тобто,
2).При множенні вектора на число його проекція на довільну вісь множиться на це число. Тобто, 
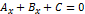 (1.1)у якому коефіцієнти А і В не дорівнюють одночасно нулю, отже
(1.1)у якому коефіцієнти А і В не дорівнюють одночасно нулю, отже  1).нехай В
1).нехай В  тоді рівняння буде мати вигляд y=
тоді рівняння буде мати вигляд y= 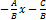 . Позначимо k=
. Позначимо k=  , b=
, b= 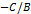 Якщо A
Якщо A  0, C
0, C  ; якщо A
; якщо A 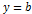 ;якщо А=0,С=0, то y=0. 2)нехай В=0, A
;якщо А=0,С=0, то y=0. 2)нехай В=0, A  . Тоді рівняння буде мати вигляд
. Тоді рівняння буде мати вигляд  . Позначимо
. Позначимо  . Якщо С
. Якщо С  ;якщо С=0, то x=0. Отже при будь-яких значеннях коефіцієнтів А,В(не рівних одночасно нулю) і С рівняння (1.1) є рівнянням деякої прямої лінії на площині Оxy. Рівняння (1.1) називається загальним рівнянням прямої.
;якщо С=0, то x=0. Отже при будь-яких значеннях коефіцієнтів А,В(не рівних одночасно нулю) і С рівняння (1.1) є рівнянням деякої прямої лінії на площині Оxy. Рівняння (1.1) називається загальним рівнянням прямої.  )паралельно вектору
)паралельно вектору 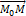 =(x-
=(x- 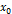 ;y-
;y- 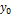 ;z-
;z-  ). Вектори
). Вектори  =
=  =
=  (1.1). Рівняння (1.1) називають канонічним рівнянням прямої. Зауважимо, що координати вектора напряму прямої Ɩ можуть бути нульовими. Тому в (1.1) можуть стояти нулі в знаменниках.
(1.1). Рівняння (1.1) називають канонічним рівнянням прямої. Зауважимо, що координати вектора напряму прямої Ɩ можуть бути нульовими. Тому в (1.1) можуть стояти нулі в знаменниках.
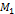 (
(
 (
( ).Розглянемо вектор
).Розглянемо вектор  =(
=( ).Тут точка M(x;y;z) довільна точка прямої. За умовою ці вектори лежать на одній прямій, а отже, колінеарні і їх координати пропорційні.
).Тут точка M(x;y;z) довільна точка прямої. За умовою ці вектори лежать на одній прямій, а отже, колінеарні і їх координати пропорційні.  (1.2). (1.2)- рівняння прямої, яка проходить через 2 відомі точки.
(1.2). (1.2)- рівняння прямої, яка проходить через 2 відомі точки. , рівняння прямої, яке проходить через дві задані точки A(a;0) B(0;b), буде мати вигляд
, рівняння прямої, яке проходить через дві задані точки A(a;0) B(0;b), буде мати вигляд  . Після перетворень
. Після перетворень 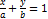 (1.1). Рівняння (1.1) називається рівнянням прямої у відрізках.
(1.1). Рівняння (1.1) називається рівнянням прямої у відрізках. . Позначимо кутовий коефіцієнт прямої k=tg α, отримаємо
. Позначимо кутовий коефіцієнт прямої k=tg α, отримаємо 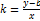 або y= kx+b (1.2). Рівняння (1.2) називається рівнянням прямої з кутовим коефіцієнтом.
або y= kx+b (1.2). Рівняння (1.2) називається рівнянням прямої з кутовим коефіцієнтом. до прямої Ɩ:
до прямої Ɩ:  знаходиться за формулою:
знаходиться за формулою:  . Відхилення точки M 1(x 1, y 1, z 1) від площини δ = x 1cosα + y 1cosβ + z 1cosγ − p;δ > 0,якщо Mi і початок координат лежать по різні сторони площини, в протилежному випадкуδ < 0. Відстань від точки до площини дорівнює | δ |. Нормальне рівняння прямої:
. Відхилення точки M 1(x 1, y 1, z 1) від площини δ = x 1cosα + y 1cosβ + z 1cosγ − p;δ > 0,якщо Mi і початок координат лежать по різні сторони площини, в протилежному випадкуδ < 0. Відстань від точки до площини дорівнює | δ |. Нормальне рівняння прямої:  , де р – відстань прямої від початку координат, α – кут, утворений з віссю Оx перпендикуляром до прямої з початку.
, де р – відстань прямої від початку координат, α – кут, утворений з віссю Оx перпендикуляром до прямої з початку. та
та  . Нехай задані дві прямі
. Нехай задані дві прямі  =
=  =
=  та
та  =
= 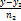 =
=  . Кут між прямими- це кут між векторами напрямку цих прямих
. Кут між прямими- це кут між векторами напрямку цих прямих  =(
=(
 =(
=( ). Тому
). Тому 
 =
=  . Прямі взаємно перпендикулярні, якщо
. Прямі взаємно перпендикулярні, якщо
 (1.1) Рівняння (1.1) називають загальним рівнянням площини. Рівняння (1.1) називають неповним, якщо один з коефіцієнтів дорівнює нулю. Розглянемо усі можливі випадки неповних рівнянь площини. 1).D=0:
(1.1) Рівняння (1.1) називають загальним рівнянням площини. Рівняння (1.1) називають неповним, якщо один з коефіцієнтів дорівнює нулю. Розглянемо усі можливі випадки неповних рівнянь площини. 1).D=0:  ,2).A=0:
,2).A=0:  , 3).B=0:
, 3).B=0:  , 4).C=0:
, 4).C=0:  , 5).A,D=0;6).B,D=0;7).C,D=0;8).A,B=0;9).A,C=0;10).C,B=0.
, 5).A,D=0;6).B,D=0;7).C,D=0;8).A,B=0;9).A,C=0;10).C,B=0. ; Рівняння площини, що проходить через точку M (x 0, y 0, z 0) перпендикулярно до вектора N(A,B,C): A (x − x 0) + B (y − y 0) + C (z − z 0) = 0; Рівняння площини, що проходить через три задані точки M (xi, yi, zi), які не лежать на одній прямій:
; Рівняння площини, що проходить через точку M (x 0, y 0, z 0) перпендикулярно до вектора N(A,B,C): A (x − x 0) + B (y − y 0) + C (z − z 0) = 0; Рівняння площини, що проходить через три задані точки M (xi, yi, zi), які не лежать на одній прямій:  ; Нормальне (нормоване) рівняння площини:
; Нормальне (нормоване) рівняння площини:  .
. 1={A1,B1,C1},
1={A1,B1,C1},