
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородного різницевого рівняння 2-го порядку iз сталими коефцієнтами.Содержание книги
Поиск на нашем сайте
Означення. Лінійним різницевим рівнянням k-го порядку називається рівняння
де b 0, b 1, b 2, …, bk — сталі коефіцієнти. Подавши оператори різниць D і через оператор зсуву S, можемо записати різницеве рівняння в рівносильній формі:
Число k називається порядком різницевого рівняння. Це
Означення. Розв’язком різницевого рівняння називається послідовність yn (n = 0, 1, 2, …), яка в результаті підставляння в різницеве рівняння (22) перетворює рівняння на тотожність. Означення. Розв’язок різницевого рівняння k -го порядку (24)
називається загальним, якщо завдяки вибору довільних сталих
завжди має розв’язок відносно сталих с 1, с 2, …, сk. Означення. Визначник системи рівнянь (26)
називається визначником Вронського. Очевидна теорема: Теорема 4.1. Для того щоб розв’язок вигляду (25) був загальним розв’язком різницевого рівняння (24), необхідно і достатньо, щоб Замінюючи n на (т + 1) у визначнику (27), дістаємо рівняння для визначника Вронського
Із рівняння (28) випливає такий результат. Теорема 4.2. Якщо в різницевому рівнянні (24), де ak ¹ 0, a 0 ¹ 0, визначник Вронського при деякому значенні n відмінний від нуля, то визначник Вронського відмінний від нуля при всіх значеннях n. Якщо визначник Вронського перетворюється на нуль при деякому значенні n, то він тотожно дорівнює нулю. Означення. Якщо для розв’язків yn = yi, n (і = 1, 2, …, k) визначник Вронського відмінний від нуля, то ці розв’язки називаються лінійно незалежними. Якщо визначник Вронського дорівнює нулю, то ці розв’язки називаються лінійно залежними. Теорема 4.3. Якщо рівняння
Доведення. Частинні розв’язки
є визначником Вандермонда і відмінний від нуля при m і ¹ m l Теорема 4.4. Якщо мультиплікаторне рівняння L (m) = 0 має корені m1, …, m l, (m 1 + …+ ml = k), то загальний розв’язок різницевого рівняння (24) подається у вигляді
Означення. Нульовий розв’язок різницевого рівняння (24) називається асимптотично стійким, якщо будь-який його розв’язок уn прямує до нуля при n ® + ¥. З теореми 4.4 випливає, що нульовий розв’язок різницевого рівняння (24) буде асимптотично стійким тоді і тільки тоді, коли всі корені мультиплікаторного рівняння L (m) = 0 будуть за модулем менші від одиниці.
Числові ряди. Основні поняття. Числові ряди. Означення: числовим рядом є вираз, який має вигляд суми нескінченої послідовності доданків: U1+U2+U3+…+Un+…(1), де U1 – перший член ряду, U2 – другий, а Un – n-член, або загальний член ряду. Утворимо так звані часткові суми ряду: S1=U1 S2=U1+U2 ………………………… Sn=U1+U2+U3+…+Un+... ………………………… Означення: Ряд (1) називають збіжним, якщо:
тобто сума існує. Ряд (1) коротко можна записати:
Якщо ряд (1) збіжний, то пишуть:
Означення: якщо:
то ряд (1) називають розбіжним рядом, такий ряд суми не має. Різницю між сумою S ряду і n-початковою сумою називають залишком ряду і позначають: Rn=S-Sn. Якщо ряд збіжний, то:
Необхідна ознака збіжності. Теорема: Якщо ряд
збіжний, то:
Доведення: Оскільки ряд збіжний, то:
поряд з цією рівністю для збіжного ряду можна записати:
Ця ознака є лише необхідною умовою збіжності. Якщо вона не виконується, то ряд розбіжний, якщо виконується, то ряд може бути як збіжним, так і розбіжним.
Властивості збіжних рядів 1. Нехай ряд
збігається до суми S. Тоді для будь-якого
теж збігається и має суму cS, тобто
Доведення випливає з означень. 2. Нехай ряди
збігаються до сум S ' та S '' відповідно. Тоді ряд
збігається до суми S ' + S '', тобто
Означення. Для ряду
та числа
називається залишком вихідного ряду. Якщо ряд (2) збігається, то rm — сума залишку. 3. Якщо ряд (1) збігається до суми S, то збігається будь-який його залишок, причому
Якщо для деякого 4. Критерій Коші збіжності числового ряду. Для того щоб ряд (1) збігався, необхідно і достатньо, щоб
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 375; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.203.104 (0.008 с.) |

 (n = 0, 1, 2 …), (21)
(n = 0, 1, 2 …), (21)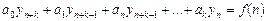 (n = 0, 1, 2 …). (22)
(n = 0, 1, 2 …). (22) (n = 0, 1, 2 …),
(n = 0, 1, 2 …), ;
;  .
. Якщо f (n) º 0, то різницеве рівняння називається однорідним. Якщо f (n) º 0, то рівняння називається неоднорідним. Для однозначного визначення розв’язку різницевого рівняння звичайно задають початкові умови:
Якщо f (n) º 0, то різницеве рівняння називається однорідним. Якщо f (n) º 0, то рівняння називається неоднорідним. Для однозначного визначення розв’язку різницевого рівняння звичайно задають початкові умови: (n = 0, 1, …, k – 1). (23)
(n = 0, 1, …, k – 1). (23) (25)
(25) (n = 0, 1, 2, …, k – 1) (26)
(n = 0, 1, 2, …, k – 1) (26) (27)
(27) (n = 0, 1, 2, …).
(n = 0, 1, 2, …). (28)
(28) має k різних коренів m1, m2, …, m k, то загальний розв’язок різницевого рівняння (24) набирає вигляду
має k різних коренів m1, m2, …, m k, то загальний розв’язок різницевого рівняння (24) набирає вигляду (n = 0, 1, 2, …).
(n = 0, 1, 2, …). (і = 1, 2, …, k) будуть лінійно незалежні, бо визначник Вронського
(і = 1, 2, …, k) будуть лінійно незалежні, бо визначник Вронського
 (31)
(31)
 (1’)
(1’)








 ряд
ряд
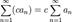 .
. та
та 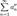

 .
.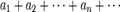 (1)
(1) ряд
ряд (2)
(2) .
. збігається залишок (2), то ряд (1) збігається.
збігається залишок (2), то ряд (1) збігається.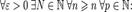
 .
. Цей критерій являє собою критерій Коші для числовой послідовності
Цей критерій являє собою критерій Коші для числовой послідовності  .
. 



