
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод зведення визначника до трикутного виглядуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Метод зведення визначника до трикутного вигляду Метод зведення визначника до трикутного вигляду полягає в тому, що, користуючись властивостями визначників, даний визначник перетворюється так, щоб одержати визначник трикутного вигляду відносно головної або побічної діагоналі, і далі одержується результат. Методом зведення до трикутного вигляду можна обчислювати визначники малих порядків. Метод виділення лінійних множників Метод використовується, коли елементи визначника можна вважати многочленами від одної або кількох змінних. В цьому випадку і самий визначник є многочленом від цих змінних.
В основі метода знаходяться наступні відомі властивості многочленів 1) многочлен від деякої змінної степеня k має не більше ніж k коренів. 2) якщо f (x) – многочлен степеня k і x =a- корінь цього многочлена, то з многочлена виноситься множник (x- 3) якщо x =a1 і x =a2 – корені многочлена f (x) степеня k, a1 ¹ a2 і, згідно з попередньою властивістю, f (x) = (x -a1) g (x), де g (x) – многочлен степеня k -1, то x =a2, є коренем многочлена g (x), а тому многочлен f (x) можна подати у вигляді f (x) = (x -a1) (x -a2) h (x), де h (x) – многочлен степеня k -2. 4) з попередньої властивості випливає, що якщо f (x) – многочлен степеня k, a1, a2,..., a k – його різні корені, то f (x) = a (x -a1) (x -a2)… (x -a k), де a – старший коефіцієнт многочлена f (x).
Властивості визначників 1. Якщо всі елементи деякого рядка визначника дорівнюють нулю (нульовий рядок), то визначник дорівнює нулю. 2. Якщо у визначнику переставляються місцями два рядки, то змінюється лише знак визначника. Припустимо, що у визначнику D міняються місцями і -й і j -й рядки (і ¹ j), тоді D = 3. Якщо два рядки визначника співпадають, то визначник дорівнює нулю. 4. Якщо деякий рядок визначника помножується на число l, то визначник помножується на l. Припустимо, що у визначнику D = помножується на l і -й рядок, тоді
З цієї властивості випливає, що якщо всі елементи деякого рядка визначника помножені на деяке число l, то це число можна винести за знак визначника як множник.
Два рядки визначника називаються пропорційними, якщо один з них можна одержати помноженням другого на деяке число.
5. Якщо два рядки визначника пропорційні, то визначник дорівнює нулю. Нехай (bi 1, bi 2,…, bin) і (сi 1, сi 2,…, сin) – два рядки. Під сумою цих рядків розуміється рядок вигляду (bi 1+ сi 1, bi 2 + сi 2,…, bin + сin). 6. Якщо у визначнику D і-рядок є сумою двох рядків, то визначник D можна розкласти в суму двох визначників D1 і D2 за і-м рядком таким чином, що і-рядком визначника D1 є перший доданок, а і-м рядком визначника D2 – другий доданок і-го рядка визначника D. Решта рядків визначників D1 і D2 співпадають з відповідними рядками визначника D. Припустимо, що у визначнику D і -й рядок є сумою двох рядків, тоді D = Аналогічно, якщо і -й рядок визначника D є сумою k рядків, то визначник D можна розкласти в суму k визначників за і -м рядком. 7. Якщо до рядка визначника додати інший рядок, помножений на число, то визначник не змінюється. Нехай 8. Якщо у визначнику деякий рядок є лінійною комбінацією інших рядків, то визначник дорівнює нулю. 9. Якщо до рядка визначника додати лінійну комбінацію інших рядків, то визначник не змінюється. Обернена матриця. Ранг матриці Обернена матриця — для кожної невиродженої квадратної матриці
де Якщо для матриці Знаходження оберненої матриці
Властивості
Ранг мáтриці (математичний) — щонайвищий з порядків відмінних від нуля мінору цієї матриці. Ранг матриці рівний найбільшому числу лінійно-незалежних рядків (або стовпців) матриці. Причому ранг по стовпцям збігається з рангом по рядкам.
Ранг матриці не міняється при елементарних перетвореннях матриці (перестановці рядків або стовпців, множенні рядка або стовпця на відмінне від нуля число і при складанні рядків або стовпців). Система лінійних рівнянь має розв'язок тоді і тільки тоді, коли ранг матриці, складеної з коефіцієнтів при невідомих, не змінюється при додаванні до неї стовпця вільних членів. Цей розв'язок єдиний, якщо цей ранг матриці дорівнює кількості невідомих. Ранг 5.Система лінійних алгебраїчних рівнянь.Їх сумісність. Система лінійних алгебраїчних рівнянь (СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:
Це система m лінійних рівнянь з n невідомими, де
Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задач лінійної алгебри, теорії диференціальних рівнянь, математичної фізики, тощо, та областей фізики й техніки, де застосовуються ці математичні теорії. Розв’язком системи лінійних алгебраїчних рівнянь є будь-яка сукупність дійсних чисел x 1, x 2,..., xn, яка при підстановці кожне рівняння системи перетворює його в тотожність. Якщо система має хоча б один розв’язок, то вона називається сумісною, і несумісною, якщо не має жодного. Відповідь на питання сумісності системи дає теорема Кронекера-Капеллі. Сумісна система називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо вона має безліч розв’язків. В останньому випадку кожен її розв’язок називають частковим розв’язком системи. Сукупність усіх часткових розв’язків називають загальним розв’язком системи. Опис методу. 1) Для системи 3 лінійних рівнянь з 3 невідомими (над довільним полем)
з визначником матриці системи Δ, що не рівний нулеві, розв'язок записується у такому вигляді:
(i-й стовпчик матриці системи замінюється стовпчиком вільних членів). 2) Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, c3 виконується рівність:
У такій формі формула Крамера справедлива без припущення, що Δ не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори b1,b2,...,bn та x1,x2,...,xn, або набір c1,c2,...,cn складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем. В такому вигляді формула Крамера використовується, наприклад, при доведенні формули для визначника Грама і Леми Накаями. Матричний запис. Векторна форма еквівалентна матричній формі запису Ax=b де A — матриця m×n, x — вектор з n компонент, b — вектор з m компонент.
Число векторів в базисі лінійної оболонки векторів є рангом матриці.
7. Розв'язрання СЛАР методом Гауса. Однорідна СЛАР. Ме́тод Га́уса — алгоритм розв'язку системи лінійних алгебраїчних рівнянь. Початок алгоритму.
Прямий хід: Шляхом елементарних перетворень рядків (додавань до рядка іншого рядка, помноженого на число, і перестановок рядків) матриця приводиться до верхньотрикутного вигляду. З цього моменту починається зворотний хід. З останнього ненульового рівняння виражаємо кожну з базисних змінних через небазисні і підставляємо в попередні рівняння. Повторюючи цю процедуру для всіх базисних змінних, отримуємо фундаментальний розв'язок.
Однорідна СЛАР Система рівнянь завжди сумісна, бо завжди має нульовий розв’язок. Цей нульовий розв’язок називається тривіальним. Якщо n>r, то система рівнянь має n-r лінійно незалежних нульових розв’язків. Ці розв’язки утворюють ядро матриці. Кут між двома площинами. Кутом між двома площинами називають один із суміжних двогранних кутів або, утворених цими площинами. Якщо площини не перетинаються, тобто паралельні, то кут між ними дорівнює 0. Тепер розглянемо задачу про обчислення кута між двома площинами. Кут між двома площинами, точніше один із суміжних кутів між двома площинами, може бути обчислений як кут між нормалями до цих площин. Якщо площини задані своїми загальними рівняннями: A1x+B1y+C1z+D1=0 A2x+B2y+C2z+D2=0, тоді їх нормальні вектори мають вигляд
Кут між прямою i площиною. Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину. Взаємне розташування прямої i площини. Коло з центром у точці М(a;b) і радіусом R – це геометричне місце точок площини, які віддалені від точки М на відстань R. Канонічне р-ня кола: Границя функції. Число А називають границею функції y=f(x), тобто При цьому кажуть, що функція “прямує” до А за умови, що її аргументи х наближаються все ближче до х0. Важливо, що сама функція в точці х0 може бути і не заданою. Число В називають границею функції y=f(x), коли Розглянемо односторонні границі для функції Правостороння границя функції:
Лівостороння границя функції:
Якщо Сталу можна виносити за знак границі: Ознаки існування границі. Для існування
Функція у=f(х) називається нескінченно малою в точці х0, якщо Функція у=f(х) називається нескінченно великою в точці х0, якщо Нехай функції у1(х) та у2(х) – безмежно малі в деякій точці х0. Тоді у1(х) називають нескінченно малою більш високого порядку, ніж у2(х) в точці х0, якщо Нехай функції у1(х) та у2(х) – безмежно малі в деякій точці х0. Тоді у1(х) та у2(х) називають еквівалентно малими в точці х0, якщо Властивості неск. мал.: 1) Алгебраїчна сума скінченого числа неск. мал.. величин є неск. мал.. величиною. 2) Добуток неск. мал.. величин на обмежену ф-ю(в тому числі на константу і на інші неск. мал.. ф-ї) є величиною неск. малою. 3) Частка від ділення неск. мал.. величин на ф=ю границі якої відміна від 0 є неск. мал.. величина. Властивості неск. вел. величин: 1) f(x) неск. вел. Величина, т. 2) f(x), φ(x) - неск. вел. Величини, f(x)+φ(x) - неск. вел. Величини 3) частка від ділення неск. вел. Величин
Первісна. Невизначений інтеграл i його властавості. Таблиця інтегралів. Означення: Функція F(x) називається первісною для ф-ії f(x) на проміжку І, якщо на цьому проміжку F`(x)=f(x) або dF(x)=f(x)dx. Із означення виходить, що первісна F(x) – диференційована, а значить неперервна функція на проміжку І, і її вигляд суттєво залежить від проміжку, на якому вона розглядається. Теорема про множину первісних: Якщо F(x) – первісна для функції f(х) на проміжку І, то: 1.F(x)+С – також первісна для f(x) на проміжку І; 2.будь-яка первісна Ф(х) для f(x) може біти представлена у вигляді Ф(х)= F(x)+С на проміжку І. (тут С=const називається довільною сталою). Озн. Сукупність всіх похідних для ф-ії f(x) на проміжку X називається невизначеним інтегралом від ф-ії f(x) і позначається Властивості, що випливають із означення невизн. інт: І. похідна від невизначеного інтеграла дорівнює підінтегральній ф-ії:
ІІ. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу. ІІІ. Властивості, що відображають основні правила інтегрування: IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла. V. Невизн. інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують. Таблиця інтегралів.
Невласні ітеграли. Невластивий інтеграл є розширенням поняття визначеного інтегралу; він дозволяє в деяких випадках обраховувати "інтеграл на нескінченості" або "інтеграл від необмеженої функції".
Згідно з теоремою існування визначеного інтеграла Н.І. існує, якщо виконані умови: 1) відрізок інтегрування [а, b] скінчений; 2) підінтегральна функція f(x) неперервна або обмежена і має скінченну кількість точок розриву. Якщо хоч би одна із умов не виконується, то визначений інтеграл називають невласним. Якщо не виконується перша умова, тобто b = ∞ або а = ∞ або а = -∞ та b = ∞, то інтеграли називають невласними інтегралами з нескінченними межами. Якщо не виконується лише друга умова, то підінтегральна функція f(x)має точки розриву другого роду на відрізку інтегрування [а, b]. В цьому випадку
Числові ряди. Означення: числовим рядом є вираз, який має вигляд суми нескінченої послідовності доданків: U1+U2+U3+…+Un+…(1), де U1 – перший член ряду, U2 – другий, а Un – n-член, або загальний член ряду. Утворимо так звані часткові суми ряду: S1=U1 S2=U1+U2 ………………………… Sn=U1+U2+U3+…+Un+... ………………………… Означення: Ряд (1) називають збіжним, якщо:
тобто сума існує. Ряд (1) коротко можна записати:
Якщо ряд (1) збіжний, то пишуть:
Означення: якщо:
то ряд (1) називають розбіжним рядом, такий ряд суми не має. Різницю між сумою S ряду і n-початковою сумою називають залишком ряду і позначають: Rn=S-Sn. Якщо ряд збіжний, то:
Необхідна ознака збіжності. Теорема: Якщо ряд
збіжний, то:
Доведення: Оскільки ряд збіжний, то:
поряд з цією рівністю для збіжного ряду можна записати:
Ця ознака є лише необхідною умовою збіжності. Якщо вона не виконується, то ряд розбіжний, якщо виконується, то ряд може бути як збіжним, так і розбіжним.
Властивості збіжних рядів 1. Нехай ряд
збігається до суми S. Тоді для будь-якого
теж збігається и має суму cS, тобто
Доведення випливає з означень. 2. Нехай ряди
збігаються до сум S ' та S '' відповідно. Тоді ряд
збігається до суми S ' + S '', тобто
Означення. Для ряду
та числа
називається залишком вихідного ряду. Якщо ряд (2) збігається, то rm — сума залишку. 3. Якщо ряд (1) збігається до суми S, то збігається будь-який його залишок, причому
Якщо для деякого 4. Критерій Коші збіжності числового ряду. Для того щоб ряд (1) збігався, необхідно і достатньо, щоб
Ознака Даламбера. Ознака Даламбера: Якщо для знакододатного ряду
існує
то, якщо: а)D>1, ряд – розбіжний б)D<1, ряд – збіжний в)D=1, –??? Зауваження. Ознаку Д’Аламбера доцільно застосувати до рядів, загальні члени яких містять показникові вирази, добутки або факторіали. Ознакою Коші зручно користуватися при дослідженні рядів, загальні члени яких містять показникові вирази.
Радикальна ознака Коші. Радикальна ознака Коші.
а)k<1, ряд – збіжний б)k>1, ряд – розбіжний в)k=1, –??? Якщо для числового ряда
з невід'ємними членами існує таке число d, 0 < d < 1, що, починаючи з деякого номера, виконується нерівність Гранична форма Умова радикальної ознаки рівносильно наступному:
Тобто можна сформулювати радикальну ознаку збіжності знакододатнього ряду у граничній формі:
Беремо ò від Un-члена ряду. Якщо невласний інтеграл збіжний, то ряд – збіжний, якщо ж розбіжний, то ряд – розбіжний. Интегральный признак Коши — признак сходимости убывающего положительного числового ряда. Признак Коши даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на
Означення: Знакопочерговий ряд – ряд вигляду:
Для дослідження знакопочергового ряду на абсолютну і умовну збіжність складається ряд з абсолютних величин. Означення: Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду. Означення: Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.
Ознака Лейбніца. Теорема: Якщо члени знакопочергового ряду спадають по абсолютній величині і границя абсолютної величини загального члена ряду = 0, то ряд збігається. Коротко цю теорему можна записати так:
Наслідок1: Знак суми збіжного знакопочергового ряду такий же, як і знак першого члену ряду. Наслідок2: Якщо знакопочерговий ряд збігається, то його сума за абсолютною величиною не перевищує перший член ряду, тобто |S|<|U1|. Наслідок3: Якщо при обчисленні суми збіжного знакопочергового ряду обмежитись тільки першими n членами, а всі інші відкинути, то похибка за абсолютною величиною не перевищить першого із відкинутих членів. Наслідок4: Якщо для ряду не виконується умова теореми Лейбніца:
то ряд є розбіжним, оскільки не виконується необхідна умова збіжності.
82. Знакозмінні ряди. Абсолютна та умовна збіжність. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на – 1.
Означення: Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається. Теорема. (Дирихле) Если ряд сходится абсолютно, то ряд полученный из него перестановкой членов, также сходится и имеет ту же сумму. Теорема. (Римана). Если ряд сходится условно, то для любого числа A можно найти такую перестановку членов ряда, что после перестановки получится ряд, имеющий своей суммой это число A или получить расходящийся ряд. 83. Поняття степеневого ряду. Теорема Абеля.

Степеневий ряд може мати вигляд: a0+a1(x-с)+a2(x-с)2+…+an(x-с)n+… Такий ряд за допомогою заміни х-с=у зводиться до звичайного степеневого ряду.
Теорема Абеля. Якщо степеневий ряд:
1) якщо при х=х0, то він абсолютно збігається для будь-якого х, що задовольняє нерівність |x|<|x0|; 2) якщо ряд розбігається при х=х1, то він розбігається при всіх х, що задовольняють нерівніст |x|>|x1|. 84. Радіус та інтервал збiжнocтi степеневого ряду. Властавості степеневих рядів.
Як наслідок із теореми Абеля для Степ. Р. існує інтервал збіжності з центром в точці х0. Означення: Інтервалом збіжності Степ. Ряду називається такий інтервал, у всіх внутрішніх точках якого ряд збігається абсолютно, а для всіх точок |x|>R ряд є розбіжним, при цьому число R>0 називається радіусом збіжності ряду. Зауваження: На кінцях інтервалу збіжності, тобто в точках x=-R, x=R ряд може як збігатись, так і розбігатись. Це питання потребує спеціального дослілження в кожному випадку. Властивості: Теорема 1 (неперервність суми степеневого ряду). Сума степеневого ряду є неперервною всередині проміжку збіжності.
Теорема 2 (диференціювання степеневих рядів). Якщо степеневий ряд має інтервал збіжності, то ряд одержаний почленним диференціюванням ряду, має той же інтервал збіжності; при цьому сума ряду де сума ряду. Наслідок. Якщо степеневий ряд збігається в інтервалі то його сума представляє собою функцію, що має всередині інтервалу збіжності похідні довільного порядку, кожна з яких є сумою ряду, одержаного в результаті почленного диференціювання даного ряду відповідне число разів; при цьому інтервал збіжності кожного ряду, одержаного в результаті диференціювання, є той же інтервал Ряд Тейлора i Маклорена. Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций. Пусть функция f (x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд
называется рядом Тейлора функции f в точке a. В случае, если a = 0, этот ряд также называется рядом Макло́рена. Свойства:
Метод зведення визначника до трикутного вигляду Метод зведення визначника до трикутного вигляду полягає в тому, що, користуючись властивостями визначників, даний визначник перетворюється так, щоб одержати визначник трикутного вигляду відносно головної або побічної діагоналі, і далі одержується результат. Методом зведення до трикутного вигляду можна обчислювати визначники малих порядків.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.119.139 (0.014 с.) |

 ), тобто многочлен подається у вигляді f (x) = (x -a) g (x), де g (x) – многочлен степеня k -1.
), тобто многочлен подається у вигляді f (x) = (x -a) g (x), де g (x) – многочлен степеня k -1. = -
= -  .
.
 = l
= l  =
= 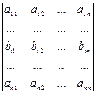 +
+  .
. ,
, 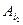 ,...,
,..., 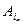 ‑ деякі рядки визначника D, а l 1, l 2,..., ln – деякі числа. Тоді рядок l 1
‑ деякі рядки визначника D, а l 1, l 2,..., ln – деякі числа. Тоді рядок l 1  , розмірності
, розмірності  , завжди існує обернена матриця, позначається
, завжди існує обернена матриця, позначається  така що:
така що:
 одинична
одинична  , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою.
, то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою. , тобто
, тобто 
 - союзна матриця.
- союзна матриця.
 — обернення транспонованої матриці
— обернення транспонованої матриці — обернення спряженої матриці
— обернення спряженої матриці для довільного коефіцієнта
для довільного коефіцієнта 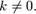

 — визначник оберненої матриці.
— визначник оберненої матриці. матриці розмірності
матриці розмірності  називають повним, якщо
називають повним, якщо  .
.
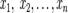 є невідомими,
є невідомими, є коефіцієнтами системи,
є коефіцієнтами системи, - вільними членами[1].
- вільними членами[1].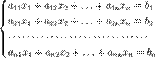




 1={A1,B1,C1},
1={A1,B1,C1}, 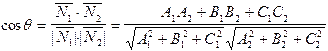
 , а між паралельними прямою та площиною таким, що дорівнює
, а між паралельними прямою та площиною таким, що дорівнює  .
. .
.
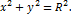
 , якщо для будь-якого ε>0 знайдеться таке δ>0, що як тільки її аргументи х попадають у δ -окіл точки х0, так одразу відповідні у=f(x) попадають в ε -окіл точки А. Іншими словами, при виконанні умови
, якщо для будь-якого ε>0 знайдеться таке δ>0, що як тільки її аргументи х попадають у δ -окіл точки х0, так одразу відповідні у=f(x) попадають в ε -окіл точки А. Іншими словами, при виконанні умови  обов′язково виконується нерівність
обов′язково виконується нерівність  .
. , тобто
, тобто  , якщо для будь-якого ε>0 існує число
, якщо для будь-якого ε>0 існує число 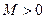 таке, що з нерівності
таке, що з нерівності 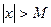 випливає нерівність
випливає нерівність  .
. , тобто коли
, тобто коли  з одного певного боку. При цьому домовимось, що позначення
з одного певного боку. При цьому домовимось, що позначення  означає наближення зліва, а позначення
означає наближення зліва, а позначення  - відповідно справа.
- відповідно справа. .
.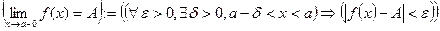 .
.  ,
,  , то
, то  ;
;  ;
;  . В останньому випадку має виконуватись умова В
. В останньому випадку має виконуватись умова В  0.
0.
 необхідно і достатньо, щоб виконувалась умова
необхідно і достатньо, щоб виконувалась умова 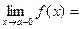
 .
. .
.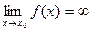 .
. . Відповідно у1(х) називають нескінченно малою більш низького порядку, ніж у2(х) в точці х0, якщо
. Відповідно у1(х) називають нескінченно малою більш низького порядку, ніж у2(х) в точці х0, якщо  .
. .
.
 , f(x) і g(x) - неск. вел. Величини.
, f(x) і g(x) - неск. вел. Величини. є величиною неск. великою.
є величиною неск. великою.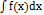 , де
, де  знак інтеграла,
знак інтеграла, 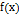 -підінтегральна ф-ія,
-підінтегральна ф-ія,  -підінтегральний вираз. Отже,
-підінтегральний вираз. Отже,  . Для існування невизначеного інтеграла для ф-ії f(x) на певному проміжку достатньо, щоб f(x) була неперервною на цьому проміжку.
. Для існування невизначеного інтеграла для ф-ії f(x) на певному проміжку достатньо, щоб f(x) була неперервною на цьому проміжку.



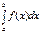 називають невласним інтегралом від розривної функції або від функції, необмеженої в точках відрізку інтегрування.
називають невласним інтегралом від розривної функції або від функції, необмеженої в точках відрізку інтегрування.
 (1’)
(1’)








 ряд
ряд
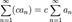 .
. та
та 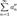

 .
.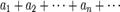 (1)
(1) ряд
ряд (2)
(2) .
. збігається залишок (2), то ряд (1) збігається.
збігається залишок (2), то ряд (1) збігається.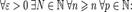
 .
. Цей критерій являє собою критерій Коші для числовой послідовності
Цей критерій являє собою критерій Коші для числовой послідовності  .
. 




 то даний ряд збігається.
то даний ряд збігається.
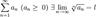
 , последний часто может быть найден в явном виде.
, последний часто может быть найден в явном виде.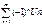


 Означення: Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.
Означення: Знакозмінний ряд називається абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду. Означення: Функціональний ряд вигляду a0+a1x+a2x2+…+anxn+… називається степеневим рядом, його загальний член Un(x)=anxn, а числа а0,а1,а2,...,аn,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:
Означення: Функціональний ряд вигляду a0+a1x+a2x2+…+anxn+… називається степеневим рядом, його загальний член Un(x)=anxn, а числа а0,а1,а2,...,аn,... – називають коефіцієнтами степеневого ряду. Степеневий ряд можна записати як:


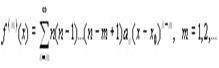 Інтервал і радіус збіжності степеневого ряду.
Інтервал і радіус збіжності степеневого ряду. Наслідок. Якщо границі інтегрування, лежать всередині інтервалу збіжності степеневого ряду, то за теоремою його можна почленно інтегрувати на проміжку, оскільки він буде рівномірно збігатися на, що містить проміжок.
Наслідок. Якщо границі інтегрування, лежать всередині інтервалу збіжності степеневого ряду, то за теоремою його можна почленно інтегрувати на проміжку, оскільки він буде рівномірно збігатися на, що містить проміжок.
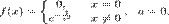 У этой функции все коэффициенты ряда Тейлора равны нулю.
У этой функции все коэффициенты ряда Тейлора равны нулю.


