
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні властивості визначників.Содержание книги
Поиск на нашем сайте
1. Значення визначника не змінюється, якщо його рядки замінити відповідними стовпцями, а стовпці – рядками. 2. Перестановка двох рядків (стовпців) визначника рівносильна множенню його на –1. 3. Якщо визначник має два однакових рядка (стовпця), то він дорівнює нулю. 4. Якщо всі елементи якого-небудь рядка (стовпця) визначника містять спільний множник, то його можна винести за знак визначника. 5. Якщо всі елементи деякого рядка (стовпця) визначника дорівнюють нулю, то і сам визначник дорівнює нулю. 6. Якщо відповідні елементи двох рядків (стовпців) визначника пропорційні, то визначник дорівнює нулю. 7. Якщо кожний елемент деякого рядка (стовпця) визначника є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких один у згаданому рядку (стовпці) має перші з заданих доданків, а інший – другі; елементи, що знаходяться на решті місць, у всіх трьох визначниках одні й ті самі. Записується ця властивість таким чином:
8. Якщо до елементів деякого рядка (стовпця) визначника додати відповідні елементи іншого рядка (стовпця), помножені на довільний спільний множник, то значення визначника при цьому не зміниться. Матриця А -1 називається оберненою до квадратної матриці А, якщо добуток цих матриць дорівнює одиничній матриці, тобто АА-1=А-1А=Е. Обернена матриця існує для всякої квадратної матриці А, яка є невиродженою, тобто коли визначник матриці detA ≠ 0. Алгоритм знаходження оберненої матриці: 1. Обчислити визначник матриці А. Якщо detA ≠ 0, то матриця А має обернену, в іншому випадку оберненої матриці не існує. 2. Обчислити алгебричні доповнення Аij елементів матриці А. 3. Визначити обернену матрицю за формулою:
Зразки розв’язування задач. 1. Знайти матрицю Розв’язання: Користуючись означеннями операцій множення матриці на число та додавання матриць, послідовно знаходимо:
2. Для матриць Р озв’язання:
3. Для заданих матриць обчислити АВ і ВА, якщо це можливо: a) Розв’язання: а) Оскільки задано матриці А2×2 і В2×2, то можна визначити добутки АВ та ВА. Отже,
АВ=ВА. б) Оскільки кількість стовпців матриці А не дорівнює кількості рядків матриці В то добутку АВ не існує. Проте можна обчислити добуток ВА.
4. Обчислити визначники: а) Розв’язання:
а) Використовуючи формулу для обчислення визначника другого порядку, маємо: б) в) Користуючись правилом трикутника, знаходимо
5. Обчислити визначник Розв’язання:
6. Обчислити визначник, спочатку спростивши його: Розв’язання: Додамо перший рядок до третього рядка, потім помножимо перший рядок на –2 і додамо його до другого рядка і отримаємо визначник, в якому елементи
7. Знайти матрицю, обернену до матриці Розв’язання: Знайдемо визначник матриці:
Перевіримо, чи виконуються рівності
Отже Завдання для самостійної роботи. 1. Для матриць 2. Обчислити визначники: а) 3. Обчислити визначник матриці, яка є добутком двох заданих матриць:
4. Серед заданих матриць знайти невироджену: а) 5. Для заданої матриці знайти обернену: 2. Системи лінійних рівнянь. Формули Крамера. Розв’язування систем лінійних рівнянь матричним методом Системою m лінійних рівнянь з n змінними x1, x2, …, xn називається система, яка має наступний вигляд: де аij – коефіцієнти при змінних; bi -вільні члени, Упорядкована сукупність чисел Система, що має розв’язок, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною. Система з єдиним розв’язком називається визначеною, а з більшим числом розв’язків – невизначаною. Система двох лінійних рівнянь з двома змінними має вигляд:
а систему трьох лінійних рівнянь з трьома змінними записують у вигляді: Метод Крамера. Цей метод розв’язування систем лінійних рівнянь зводиться до обчислення визначників. Так, розв’язок системи (2.1) можна знайти за формулами Крамера:
де
Формули Крамера для системи (2.2) мають вигляд:
де
Системи (2.1) і (2.2) мають: а) єдиний розв’язок, коли б) безліч розв’язків, коли в) не мати жодного розв’язку, коли
|
|||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.007 с.) |

 .
. .
. С=2А-3В, якщо
С=2А-3В, якщо 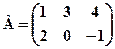 і
і 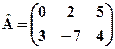 .
.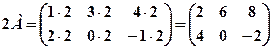 ,
,  ,
,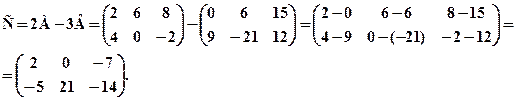
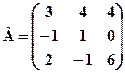 і
і 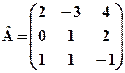 обчислити АТ+ВТ.
обчислити АТ+ВТ.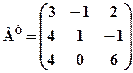 ,
,  ,
, .
. ,
, 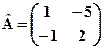 ; б)
; б) 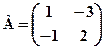 ,
, 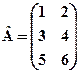 .
.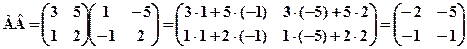 ;
;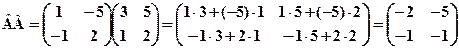 ;
; .
.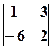
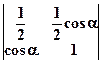 ; в)
; в) 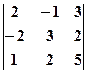 .
.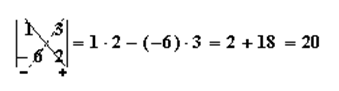
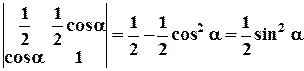 .
.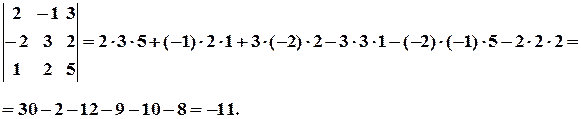
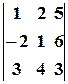 , розклавши його за елементами першого рядка.
, розклавши його за елементами першого рядка.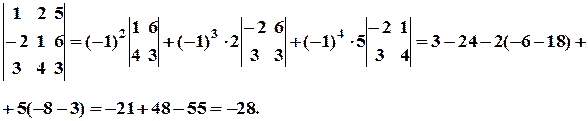
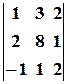 .
.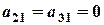 . Отриманий визначник розкладаємо за елементами першого стовпця:
. Отриманий визначник розкладаємо за елементами першого стовпця:
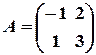 і перевірити, чи справджуються рівності
і перевірити, чи справджуються рівності 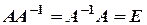 .
. .Оскільки
.Оскільки 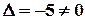 , обернена матриця
, обернена матриця  існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:
існує. Знаходимо алгебричні доповнення: А11= 3, А12= -1, А21 = -2, А22 = 1. Тоді обернена матриця буде мати вигляд:  .
.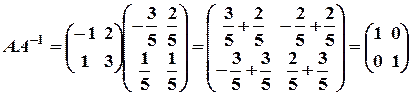 ;
;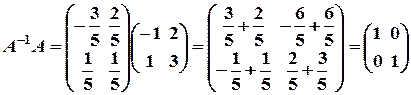 .
. і
і  обчислити АТ-3В, АВ, ВА, АВ+Е.
обчислити АТ-3В, АВ, ВА, АВ+Е.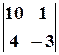 , б)
, б) 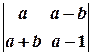 , в)
, в)  , г)
, г) 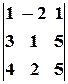 .
.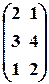 ,
, 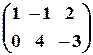 .
.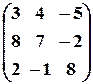 , б)
, б) 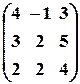 , в)
, в) 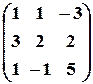 .
.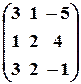 .
.
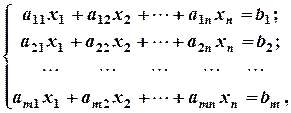
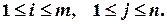
 , називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.
, називається розв’язком системи, якщо при заміні х1 на а1, х2 на а2, …, хn на аn у кожному рівнянні системи дістанемо n правильних числових рівностей.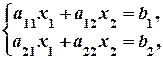 (2.1)
(2.1)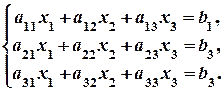 (2.2)
(2.2)
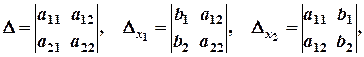 за умови, що
за умови, що 
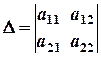 - називається визначником системи (2.1), а
- називається визначником системи (2.1), а  - визначники, які дістають з визначника
- визначники, які дістають з визначника 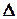 заміною першого, другого стовпців відповідно стовпцем вільних членів.
заміною першого, другого стовпців відповідно стовпцем вільних членів.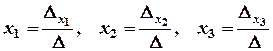 ,
,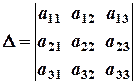
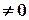 - визначник системи (2.2), а
- визначник системи (2.2), а визначники, які дістають з визначника
визначники, які дістають з визначника  ;
;
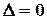 і хоча б один із визначників
і хоча б один із визначників 
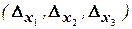 відмінний від нуля.
відмінний від нуля.


