
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нескінченна числова послідовність. Границя числової послідовності і її властивості. Нескінченно малі і нескінченно великі послідовності.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нескінченною числовою послідовністю називається числова функція, визначена на множині N натуральних чисел. Послідовність Послідовність Спадні, зростаючі, неспадні і незростаючі послідовності називаються монотонними. Звичайно послідовність задається формулою, яка виражає загальний член послідовності через n. Число а називається границею послідовності Послідовність може мати лише одну границю. Якщо послідовність має границю, то таку послідовність називають збіжною, а послідовність, яка не має границі, називається розбіжною.
Властивості числових границь мають вигляд: Теорема 1. Якщо послідовності Теорема 2. Якщо послідовності Теорема 3. Сталий множник можна винести за знак границі, якщо послідовність Теорема 4. Якщо послідовності Послідовність називається нескінченно малою, якщо її границя дорівнює нулю. Для нескінченно малих послідовностей справедливі наступні теореми: Теорема І. Сума двох нескінченно малих послідовностей є нескінченно малою. Теорема ІІ. Добуток обмеженої послідовності на нескінченно малу є нескінченно малою. Теорема ІІІ. Щоб виконувалася рівність Послідовність називається нескінченно великою, якщо
Зразки розв’язування задач. Обчислити границі таких послідовностей: 1) Чисельник і знаменник не мають границі, бо це необмежені послідовності, отже теорему про границю частки безпосередньо застосувати не можна. Поділивши чисельник і знаменник на n і застосувавши потім теорему про границю частки, дістанемо:
Решта границь 2-5 обчислюється аналогічно (чисельник і знаменник ділимо на n у старшому ступені): 2) 3) 4) 5) 6) При
Решта границь 7,8 обчислюється аналогічно. 7)
8)
9) Чисельник і знаменник не мають границі, бо це необмежені послідовності, які утворюють суми арифметичних прогресій. У чисельнику така сума
Завдання для самостійної роботи. Обчислити границі послідовностей: 1. 2. 3. 4. 5.
Похідна функції. Похідні основних елементарних функцій. Основні правила диференціювання. Похідною функції
Наводимо таблицю похідних основних елементарних функцій.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. При знаходженні похідної функції користуються також основними правилами диференціювання. 1. 2. 3. 4. Якщо у є функція від Похідна складеної функції дорівнює добутку її похідної за проміжним аргументом на похідну цього аргументу за незалежною змінною:
Якщо функція у від х задана параметричними рівняннями Геометричний зміст похідної
Другою похідною функції
Друга похідна параметрично заданої функції обчисляється за формулою:
Зразки розв’язування задач Задача 1. Знайти похідні функцій: 1) 4) Розв’язання. 1) Винесемо сталий множник за знак похідної, а потім застосуємо формулу 2 таблиці похідних
Аналогічно дістанемо: 2) 3) 4) 5)
Задача 2. Знайти похідні функції: 1) 2) 3) 4) 5) Розв’язання. 1) Знайдемо похідну від алгебраїчної суми як алгебраїчну суми похідних доданків:
2) 3) Знайдемо похідну за основним правилом 3:
4) Використаємо правило 4:
5)
Задача 3. Знайти похідні складених функцій:
1) 2) 3) 4) 5)
Розв’язання. 1) Знайдемо похідну від першого доданку за формулою:
Тоді
Похідну від другого доданку знайдемо аналогічно:
Загалом
2)
3)
4)
5)
Задача 4. Обчислити значення похідної функції Розв’язання:
Задача 5. Знайти похідну параметрично заданої функції:
Розв’язання. Знайдемо
Задача 6. Знайти похідну неявно заданої функції: 1) 2) 1) Диференціюємо по х ліву і праву частину рівняння, враховуючи, що y – це функція від х:
Розв’язуємо рівняння відносно
2) Диференціюємо по х:
Задача 7. Скласти рівняння дотичних до кривих: 1) 2) 3)
Розв’язання: 1) Знайдемо кутовий коефіцієнт дотичної до кривої:
а також Підставимо в рівняння дотичної:
2)
Знайдемо координати точки М0, через яку проведена дотична: Рівняння дотичної
3) Знайдемо похідну неявної функції:
Рівняння дотичної:
Задача 8. Знайти похідну другого порядку функції: 1) 2) 3) Розв’язання: 1) Знайдемо
2)
3)
Диференціюємо по х ще раз, а потім підставимо замість
Завдання для самостійної роботи. 1. Знайти похідні функцій: 1) 2) 3) 4) 2. Обчислити значення похідної 3. Знайти похідні параметричної і неявної функцій: 1) 2) 4. Скласти рівняння дотичних до кривих: 1) 2) 3) 5. Знайти другі похідні функцій: 1) 2) 3)
Література 1. Вища математика: основні означення, приклади і задачі: У двох книгах/ За редакцією Г.Л.Кулініча та І.П.Васильченка.- К.: Либідь, 1994. 2. Дубовик В.П., Юрик І.І. Вища математика.- К.: Вища школа, 1993. 3. Богомолов М.В. Практичні заняття з математики.- К.: Вища школа, 1979. 4. Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1.-М.:Наука, 1976. 5. Берман Г.Н. Сборник задач по курсу математического анализа.- М.:Наука, 1975.
Зміст Вступ 3 1. Матриці і операції над ними. Визначники матриць. Властивості визначників. Обернена матриця. 4 2. Системи лінійних рівнянь. Формули Крамера. Розв’язування систем лінійних рівнянь матричним методом 11 3. Вектори в просторі. Основні поняття. Лінійні операції з векторами. Прямокутна система координат у просторі. 16 4. Скалярний, векторний, мішаний добутки векторів. Застосування в задачах геометрії. Умови перпендикулярності та компланарності векторів. 23 5. Загальне і канонічне рівняння прямої. Рівняння прямої у відрізках на осях. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, яка проходить через дві дані точки. Перетин двох прямих. 29 6. Кут між двома прямими. Пучок прямих, які проходять через дану точку. Нормальне рівняння прямої. Відстань від точки до прямої. 34 7. Криві другого порядку: коло, еліпс. 38 8.Криві другого порядку: гіпербола, парабола. 42 9. Рівняння площини в просторі. 52 10. Пряма в просторі. Площина і пряма. 55 11. Нескінченна числова послідовність. Границя числової послідовності і її властивості. Нескінченно малі і нескінченно великі послідовності. 59 12. Похідна функції. Похідні основних елементарних функцій. Основні правила диференціювання. 63 Література 71
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 835; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.172.133 (0.013 с.) |

 називається зростаючою (спадною), якщо для будь-якого n виконується нерівність
називається зростаючою (спадною), якщо для будь-якого n виконується нерівність  .
. .
.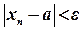 . Записується таким чином:
. Записується таким чином:  .
. збігаються, то
збігаються, то 



 , де
, де  - нескінченно мала послідовність.
- нескінченно мала послідовність. .
. .
. .
. .
. .
.
 .
. ;
; послідовність
послідовність  є різницею двох нескінченно великих послідовностей
є різницею двох нескінченно великих послідовностей  . Помноживши і поділивши послідовність на вираз
. Помноживши і поділивши послідовність на вираз  , дістанемо:
, дістанемо:




 ;
; дорівнює
дорівнює  . У знаменнику така сума
. У знаменнику така сума  , або
, або  . Тоді дана границя має вигляд:
. Тоді дана границя має вигляд:



 ;
;
 в точці
в точці  називається границя відношення приросту функції
називається границя відношення приросту функції  функції в цій точці до приросту
функції в цій точці до приросту  аргументу, коли приріст аргументу прямує до нуля:
аргументу, коли приріст аргументу прямує до нуля:




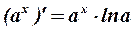











 , де с – стала.
, де с – стала. , де
, де  - функція.
- функція. .
. .
. , де
, де  , тобто залежить від х через проміжний аргумент
, тобто залежить від х через проміжний аргумент  .
. .
. ,
,  (
( - параметр), похідна
- параметр), похідна  обчисляється за формулою
обчисляється за формулою  .
. у точці
у точці  у тому, що вона дорівнює кутовому коефіцієнту дотичної до кривої
у тому, що вона дорівнює кутовому коефіцієнту дотичної до кривої  у точці з абсцисою
у точці з абсцисою  .
. .
. .
. , 2)
, 2)  , 3)
, 3)  ,
, , 5)
, 5)  .
. .
. .
. .
. .
. .
. ;
; ;
; ;
; ;
; .
.
 .
. .
.
 .
.
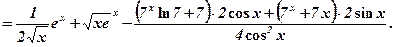
 ;
; ;
; ;
; ;
; .
. , де
, де  .
. .
.
 .
. .
.
 .
.

 .
.

 =
= .
.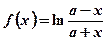 у точці х=2а.
у точці х=2а.

 .
. ,
,  .
. ;
; ;
; .
. ;
; .
.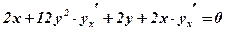 .
. .
. ;
; .
. ;
; ;
; ;
; ;
;
 .
. у точці з абсцисою
у точці з абсцисою  ;
; у точці де,
у точці де,  ;
; у точці
у точці  .
. ,
,  ,
, .
. ;
; ;
; .
.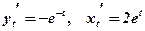 .
. ;
; .
. ,
,  .
. ;
; .
. ;
;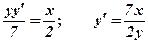 ;
; .
. ;
; ;
; .
. ;
; ;
; .
. ;
; .
. ;
; ;
;  ;
; .
. ;
; ;
; .
. ;
; ;
; ;
; 
 ;
; .
. її вираз через х.
її вираз через х. .
. ;
; ;
; ;
; .
. функції
функції  .
. ;
; .
. у точці з абсцисою х0=0;
у точці з абсцисою х0=0; ;
; у точці М(0;1).
у точці М(0;1).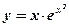 ;
;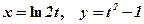 ;
; .
.


