
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальне і канонічне рівняння прямої. Рівняння прямої у відрізках на осях. Рівняння прямої з кутовим коефіцієнтом. Рівняння прямої, яка проходить через дві дані точки. Перетин двох прямих.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рівняння вигляду
Нехай
називається канонічним рівнянням прямої. Рівняння прямої у відрізках на осях має вигляд:
де Рівняння прямої з кутовим коефіцієнтом має вигляд: де Рівняння прямої, що проходить через дві дані точки Якщо дано дві прямі Зразки розв’язування задач. Задача 1. Перевірити, чи належать точки Розв’язання. Якщо координати точки задовольняють рівнянню, тобто перетворюють його в тотожність, то ця точка належить заданій прямій; якщо координати точки не задовольняють рівнянню, то точка не належить прямій. Підставивши замість змінних Задача 2. Побудуйте прямі: a) б) в) Розв’язання.
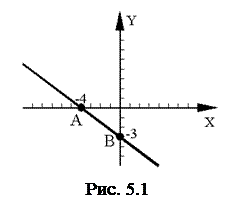
а) Щоб побудувати пряму, знайдемо координати точок перетину з осями  і і  . Припустивши, що . Припустивши, що  , дістанемо , дістанемо 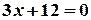 , ,  , ,  . При . При  дістанемо дістанемо 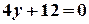 , ,  , ,  . Через точки . Через точки  і і  проводимо шукану пряму (рис. 5.1). проводимо шукану пряму (рис. 5.1).
б) Знайдемо змінну
в) Знайдемо змінну  з рівняння з рівняння 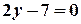 : : 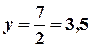 . .
На осі  візьмемо точку візьмемо точку 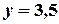 і проведемо пряму паралельно осі і проведемо пряму паралельно осі  (рис. 5.3) (рис. 5.3)
Задача 3. Складіть рівняння прямої, що проходить через точку Розв’язання. Використовуючи канонічне рівняння прямої, маємо Доводимо рівняння до загального вигляду:
Задача 4. Загальне рівняння прямої Розв’язання. Перетворимо рівняння: Тоді
Тобто  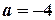 і і  . Отже дістанемо точки . Отже дістанемо точки  і і  . Пряма, яка проведена через точки . Пряма, яка проведена через точки 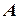 і і  - шукана (рис. 5.4). - шукана (рис. 5.4).
Задача 5. Обчислить кутовий коефіцієнт прямої Розв’язання. Розв’язавши рівняння
Розв’язання. Щоб скласти шукане рівняння прямої, треба знайти Задача 7. Складіть рівняння прямої, яка проходить через точки Розв’язання. За умовою задачі: Задача 8. Трикутник задано вершинами: Розв’язання. Знайдемо координати точки
Отже, координати точки дорівнюють
Задача 9. Знайдіть вершини трикутника, якщо його сторони задано рівняннями. Розв’язання. Щоб знайти координати вершин трикутника, треба розв’язати три системи рівнянь:
Перша система має розв’язок:
Друга система має розв’язок:
Третя система має розв’язок:
Отже, вершинами трикутника є точки Завдання для самостійної роботи. 1. При якому значенні коефіцієнта 2. Пряма проходить через точку 3. Дано рівняння сторін трикутника: 4. На прямій 5. Складіть рівняння прямої, яка перпендикулярна до даного вектора і проходить через точку перетину даних прямих: a) b) 6. Кут між двома прямими. Пучок прямих, які проходять через дану точку. Нормальне рівняння прямої. Відстань від точки до прямої. Кут
Якщо прямі задані рівняннями Умова паралельності двох прямих: Умова перпендикулярності двох прямих: Рівняння пучка прямих, які проходять через дану точку Нормальне рівняння прямої Відстань від точки Зразки розв’язування задач. Задача 1. Знайти гострий кут між прямими: 1) 2) Розв’язання. 1) Кутові коефіцієнти даних прямих дорівнюють 2) Косинус кута між прямими беремо за модулем: Задача 2. Дано трикутник з вершинами Розв’язання. Знаходимо кутові коефіцієнти сторін цього трикутника:
Знайдемо кути трикутника:
Задача 3. Які з прямих паралельні?
Розв’язання. Паралельні прямі мають однакові кутові коефіцієнти. Знайдемо кутові коефіцієнти прямих: Задача 4. Складіть рівняння прямої, яка проходить через точку Розв’язання. Знайдемо кутовий коефіцієнт даної прямої: Оскільки дана і шукана прямі паралельні, то їх кутові коефіцієнти рівні, тобто Задача 5. При якому значенні параметра Розв’язання. Кутові коефіцієнти перпендикулярних прямих зв’язані між собою співвідношенням: Задача 6. Перевірте, чи перпендикулярні прямі: 1) 2) 3) Розв’язання. 1) Перевіримо виконання умови 2) Якщо прямі задані рівняннями з кутовими коефіцієнтами, то умова перпендикулярності має вигляд: 3) Рівняння першої прямої запишемо у вигляді: Задача 7. Складіть рівняння прямої, яка проходить через точку Розв’язання. Знайдемо кутовий коефіцієнт даної прямої: Задача 8. Знайдіть відстань від точки Розв’язання. Використовуючи формулу для обчислювання відстані від точки до прямої, дістанемо:
Задача 9. Знайдіть відстань між двома паралельними прямими Розв’язання. Знайдемо будь-яку точку на першій прямій. Якщо візьмемо Завдання для самостійної роботи. 1.Складіть рівняння прямих, які проходять через точку 2.Знайдіть рівняння двох перпендикулярів до прямої 3.Трикутник задано вершинами 4. Дві протилежні вершини квадрата лежать у точках
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 5095; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.224 (0.011 с.) |

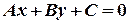 за умови, що коефіцієнти
за умови, що коефіцієнти 


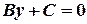




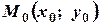 - задана точка прямої, а
- задана точка прямої, а  - вектор, колінеарний прямій:
- вектор, колінеарний прямій:

 і
і  - відповідно абсциса і ордината точки перетину прямої з осями
- відповідно абсциса і ордината точки перетину прямої з осями  ,
, - кутовий коефіцієнт, який дорівнює тангенсу кута нахилу прямої до додатного напряму осі
- кутовий коефіцієнт, який дорівнює тангенсу кута нахилу прямої до додатного напряму осі  і
і  , має вигляд:
, має вигляд:  .
. і
і  , які перетинаються, то щоб визначити координати точки перетину цих прямих, треба розв’язати систему рівнянь:
, які перетинаються, то щоб визначити координати точки перетину цих прямих, треба розв’язати систему рівнянь: 
 ,
, 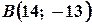 ,
,  ,
,  прямій
прямій  .
. і
і 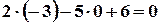 , отже точка
, отже точка  належить прямій, а точки
належить прямій, а точки  не належать.
не належать. ;
;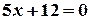 ;
;
 . На осі
. На осі  і проведемо пряму паралельно осі
і проведемо пряму паралельно осі 

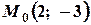 і паралельна вектору
і паралельна вектору  .
.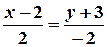 .
. ;
;  ;
;  .
. перетворити в рівняння у відрізках на осях та побудувати пряму.
перетворити в рівняння у відрізках на осях та побудувати пряму. . Праву та ліву частини рівняння розділимо на
. Праву та ліву частини рівняння розділимо на  :
:  .
. - рівняння у відрізках на осях.
- рівняння у відрізках на осях.
 .
. , звідки
, звідки  .
. і утворює з віссю
і утворює з віссю  і
і  . Для визначення
. Для визначення 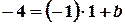 , звідки
, звідки  . Шукане рівняння має вигляд
. Шукане рівняння має вигляд  .
. і
і 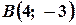 .
. ,
, 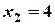 ,
,  ,
,  . Підставивши ці значення в рівняння прямої, яка проходить через дві точки, дістанемо:
. Підставивши ці значення в рівняння прямої, яка проходить через дві точки, дістанемо:  ;
;  і
і 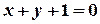 .
. ,
,  .і
.і  . Складіть рівняння медіани
. Складіть рівняння медіани  .
.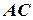 :
: ;
;  ;
; ;
;  .
. . Тоді рівняння сторони
. Тоді рівняння сторони 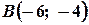 , має вигляд:
, має вигляд:  ;
; ;
; ;
; ;
;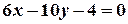 ;
; .
. ;
;  ;
;  .
.
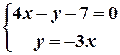
 .
.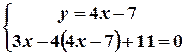






 .
.
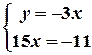
 .
.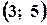 ;
;  ;
;  .
. проходить через точку перетину прямих
проходить через точку перетину прямих  і
і  .
. і утворює з віссю
і утворює з віссю  . Знайдіть на цій прямій точку з абсцисою
. Знайдіть на цій прямій точку з абсцисою 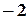 .
.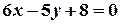 ;
;  і
і  . Знайдіть рівняння його медіан.
. Знайдіть рівняння його медіан. знайдіть точку, яка лежить від осі в три рази далі, ніж від осі
знайдіть точку, яка лежить від осі в три рази далі, ніж від осі  ,
, 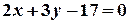 ;
;  .
. ;
;  ;
;  .
. між двома прямими, які задані загальними рівняннями
між двома прямими, які задані загальними рівняннями  і
і 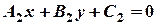 , обчислюється за формулою:
, обчислюється за формулою: .
. і
і  , то кут між прямими обчислюється за формулою
, то кут між прямими обчислюється за формулою  .
.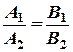 ;
;  .
. ;
; 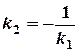 .
. , має вигляд:
, має вигляд: 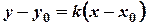 .
. одержуємо з загального рівняння
одержуємо з загального рівняння 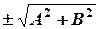 і вибрати знак протилежний знаку
і вибрати знак протилежний знаку  .
. і
і  .
. і
і  .
.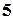 і
і 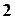 . Тангенс куту між прямими беремо за модулем:
. Тангенс куту між прямими беремо за модулем:  . Отже
. Отже  .
. . Отже
. Отже  .
. ,
, 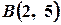 і
і  . Знайдіть внутрішні кути цього трикутника.
. Знайдіть внутрішні кути цього трикутника.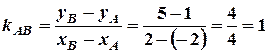 ;
;  ;
; .
. ;
;  ;
;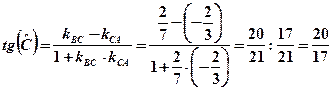 . Отже
. Отже  ;
;  ;
; 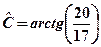 .
. ;
;  ;
;  ;
;  .
. ;
; 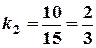 ;
;  ;
;  . Таким чином,
. Таким чином,  , а це означає, що перша та друга прямі – паралельні.
, а це означає, що перша та друга прямі – паралельні. паралельно прямій
паралельно прямій  .
. ;
;  ;
; 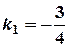 .
. . Шукана пряма проходить через точку
. Шукана пряма проходить через точку  . Тоді її рівняння запишемо у вигляді:
. Тоді її рівняння запишемо у вигляді:  , або
, або  .
. і
і  перпендикулярні?
перпендикулярні? . Для даних прямих:
. Для даних прямих:  . Звідки,
. Звідки,  .
.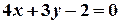 ;
; і
і  ;
; і
і  .
. . Для даних прямих:
. Для даних прямих:  ;
;  ;
;  ;
;  . Тоді
. Тоді 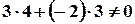 . Це означає, що прямі неперпендикулярні.
. Це означає, що прямі неперпендикулярні.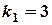 ;
;  . Умова перпендикулярності не виконується, отже, прямі неперпендикулярні.
. Умова перпендикулярності не виконується, отже, прямі неперпендикулярні. . Тоді
. Тоді  . Друга пряма має кутовий коефіцієнт:
. Друга пряма має кутовий коефіцієнт: 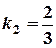 . Умова перпендикулярності виконується:
. Умова перпендикулярності виконується: 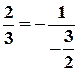 ;
;  . Прямі перпендикулярні.
. Прямі перпендикулярні. перпендикулярно до прямої
перпендикулярно до прямої  .
. . Тоді кутовий коефіцієнт шуканої прямої
. Тоді кутовий коефіцієнт шуканої прямої 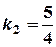 . Отже її рівняння має вигляд
. Отже її рівняння має вигляд  , або
, або  .
. до прямої
до прямої  .
. .
. і
і  .
. . Тоді
. Тоді  . Таким чином, точка
. Таким чином, точка  належить першій прямій. Отже, відстань від цієї точки до прямої
належить першій прямій. Отже, відстань від цієї точки до прямої  .
. під кутом
під кутом 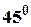 до прямої
до прямої 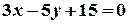 .
. у точках перетину її з осями координат.
у точках перетину її з осями координат. ,
,  і
і  . Знайдіть: кути
. Знайдіть: кути  і
і  ;рівняння висоти, яка проведена з вершини
;рівняння висоти, яка проведена з вершини  , який проходить через вершину
, який проходить через вершину  і
і 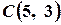 .Складіть рівняння сторін і діагоналей цього квадрата.
.Складіть рівняння сторін і діагоналей цього квадрата.


