
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння площини в просторі.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рівняння площини, що проходить через дану точку
Рівняння
називається загальним рівнянням площини, якщо коефіцієнт А,В,С одночасно не дорівнюють нулю. Ненульовий вектор Розглянемо окремі випадки загального рівняння площини. 1. Нехай D=0. Тоді рівняння площини має вигляд 2. Нехай С = 0. Тоді рівняння площини має вигляд 3. Нехай С = D = 0. Тоді рівняння площини має вигляд 4. Нехай В = С = 0. Тоді рівняння площини має вигляд 5. Нехай В=С=D=0. Тоді рівняння площини має вигляд Аналогічно при А=В=D=0 і А=С=D=0 дістанемо площини z=0 і y=0, які збігаються відповідно з координатними площинами Охy і Охz. Кут між двома площинами, які перетинаються,
Щоб дві площини були паралельні, їх нормальні вектори
Щоб площини були перпендикулярні, їх нормальні вектори
Відстань від точки M0(x0;y0;z0) до площини
Зразки розв’язування задач. Задача 1. Скласти рівняння площини, яка проходить через точку К (2;0;-1) і перпендикулярна до осі Ох. Розв’язання. Рівняння площини, перпендикулярної до осі Ох, має вигляд Ах+D =0. Підставивши в це рівняння координати точки К, знаходимо 2А+D =0, тобто D= - 2А. Підставивши тепер значення D в рівняння Ах+D =0, дістанемо Ах-2А =0, тобто х-2 =0.
Задача 2. Скласти рівняння площини, яка проходить через вісь Оz і через точку М (2;-5;4). Розв’язання. Рівняння шуканої площини має вигляд Ах+Ву=0. Підставивши в це рівняння координати точки М, дістанемо 2А-5В=0, тобто
Задача 3. Скласти рівняння площини, яка паралельна осі Ох і проходить через точки М1(3;-1;2) і М2(-2;3;4). Розв’язання. Оскільки шукана площина паралельна осі Ох і проходить через точки М1(3;-1;2) і М2(-2;3;4), то за її нормальний вектор
Скористаємось рівнянням площини, яка проходить через дану точку М2(-2;3;4) перпендикулярно до вектора 2(у-3) -4(z-4) = 0 або y-2z+5 = 0.
Задача 4. Скласти рівняння площини, яка проходить через точку М(4;-3;1) і паралельна до площини 3х+2у-4z+12=0. Розв’язання. Оскільки шукана площина паралельна площині 3х+2у-4z+12=0, то за її нормальний вектор можна взяти вектор 3(x-4)+2(y+3)-4(z-1)=0 або 3x+2y-4z-2=0.
Задача 5. Скласти рівняння площини, яка проходить через точки М1(2;-4;1) і М2(-3;5;7) і перпендикулярна до площини 3х+4у-7z+2= 0. Розв’язання. За нормальний вектор
Скористаємось рівнянням площини, яка проходить через дану точку М1(2;-4;1) перпендикулярно до вектора -87(x-4)-17(y+3)-47(z-1)= 0 або 87x+17y+47z-153=0. Задача 6. Знайти гострий кут між площинами 2x-3y+4z-1=0 і 3x-4y- z+3=0. Розв’язання. Щоб обчислити гострий кут φ між площинами, скористаємось формулою (9.3), причому праву частину рівності беремо за абсолютною величиною, бо cos φ>0. Маємо: А1=2, В1=-3, С2=4 і А2=3, В2=-4, С2=-1. Отже Тоді, використовуючи таблиці Брадіса, маємо φ=59021'.
Задача 7. Знайти відстань від точки А(-5;2;-1) до площини 2х+2у-3z-5=0. Розв’язання. Відстань від точки до площини знаходиться за формулою (9.4). Маємо:
Задача 8. Знайти відстань між паралельними площинами 2х-3у+z-2=0 і 4х-6у+2z+7=0. Розв’язання. Щоб знайти шукану відстань, треба визначити точку, яка належить одній з двох даних площин. Розглянемо площину 4х-6у+2z+7=0. Якщо х=0, у=0, то z=-3,5, тобто точка А(0;0;-3,5) належить площині. Тоді треба знайти відстань від точки А до площини 2х-3у+z-2=0. За формулою (9.4) маємо:
Задача 9. Скласти рівняння площини, яка проходить через точки А(1;2;-3), В(3;-1;2) і С(5;-3;4). Розв’язання. Нехай точка M(x;y;z) належить до шуканої площини. Складемо три вектори, які будуть виходити з точки А:
Так як вектори належать одній площині, то вони компланарні. За умовою компланарності
Тобто 2х+3у+z-5=0 є рівнянням шуканої площини.
Завдання для самостійної роботи. Задача 1. Складіть рівняння площини, яка проходить через точку M(-2;3;1) і вісь Оz. Задача 2. Складіть рівняння площини, яка проходить через точки А(2;1;-2), і В(3;0;4) і перпендикулярна до площини х+2у-z=0. Задача 3. Обчисліть кут між площинами 2х-3у+5z-2=0 і х-у+z=0. Задача 4. Знайти відстань між паралельними площинами 2х-3у+z-4=0 і 4х-6у+2z+10=0. Задача 5. Складіть рівняння площини, яка проходить через точку M(1;-3;2) паралельно двом векторам:
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 7942; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.3.204 (0.006 с.) |

 в заданому напрямі
в заданому напрямі  має вигляд:
має вигляд: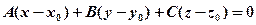 . (9.1)
. (9.1) (9.2)
(9.2) і площина проходить через початок координат.
і площина проходить через початок координат. і площина паралельна осі Oz. Аналогічно при А =0 і В = 0 дістанемо площини
і площина паралельна осі Oz. Аналогічно при А =0 і В = 0 дістанемо площини 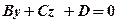 і
і  , паралельні відповідно осям Ох і Оy.
, паралельні відповідно осям Ох і Оy. і площина проходить через початок координат і паралельна осі Oz. Аналогічно при А = D = 0 і B = D = 0 дістанемо площини
і площина проходить через початок координат і паралельна осі Oz. Аналогічно при А = D = 0 і B = D = 0 дістанемо площини 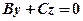 і
і 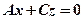 , які проходять відповідно через осі Ох і Oy.
, які проходять відповідно через осі Ох і Oy. і площина паралельна осям Oy і Oz, тобто перпендикулярна до осі Ох. Аналогічно при А = В = 0 і А=С= 0 дістанемо площини
і площина паралельна осям Oy і Oz, тобто перпендикулярна до осі Ох. Аналогічно при А = В = 0 і А=С= 0 дістанемо площини  і
і  , які перпендикулярні відповідно до осей Oz і Oy.
, які перпендикулярні відповідно до осей Oz і Oy. , тобто х=0; площина збігається з площиною Оyz.
, тобто х=0; площина збігається з площиною Оyz. і
і 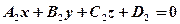 дорівнює куту між її нормальними векторами
дорівнює куту між її нормальними векторами  і
і  і обчислюється за формулою:
і обчислюється за формулою: . (9.3)
. (9.3) і
і  повинні бути колінеарні, тобто
повинні бути колінеарні, тобто .
. і
і  також повинні бути перпендикулярні, тобто
також повинні бути перпендикулярні, тобто .
. обчислюється за формулою:
обчислюється за формулою: (9.4)
(9.4)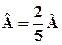 . Підставивши тепер значення В в рівняння Ах+Ву=0, знаходимо
. Підставивши тепер значення В в рівняння Ах+Ву=0, знаходимо  , тобто
, тобто 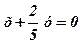 або 5х+2у=0.
або 5х+2у=0. можна взяти вектор перпендикулярний до векторів
можна взяти вектор перпендикулярний до векторів 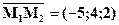 і
і  (одиничний вектор на осі Ох). З другого боку, відомо, що векторний добуток двох векторів є вектор, перпендикулярний до векторів співмножників, тому за
(одиничний вектор на осі Ох). З другого боку, відомо, що векторний добуток двох векторів є вектор, перпендикулярний до векторів співмножників, тому за  можна взяти векторний добуток
можна взяти векторний добуток 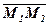 і
і  .
. . Маємо:
. Маємо: . Використавши тепер рівняння площини, що проходить через дану точку в заданому напрямі, дістанемо:
. Використавши тепер рівняння площини, що проходить через дану точку в заданому напрямі, дістанемо: шуканої площини візьмемо векторний добуток векторів
шуканої площини візьмемо векторний добуток векторів  і
і 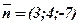 :
:
 :
: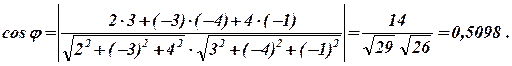
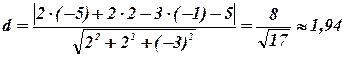 (од.).
(од.). (од.).
(од.).
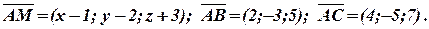
 , маємо:
, маємо: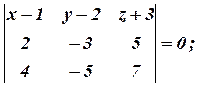

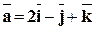 і
і  .
.


