
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння прямої з кутовим коефіцієнтом.Содержание книги
Поиск на нашем сайте Білет 17 1. Ве́кторний (ліні́йний) про́стір — основне поняття лінійної алгебри, узагальнення множини всіх векторів на площині чи в просторі з операціями додавання векторів та множення вектора на скаляр. Означення 8. Лінійно залежними називають вектори, якщо існує хоч би одне дійсне число (і = 1,2,…, n), що не дорівнює нулю і виконується рівність Означення 9. Лінійно незалежними називають вектори, якщо рівність (7) виконується тільки тоді, коли усі. В системі векторів a1,a2…an число лінійно незалежних векторів дорівнює рангу матриці, яка складена з координат цих векторів. Дійсно, якщо систему векторів a1,a2…an із простору Еm розглядати як матриці-стовпці з m заданими елементами, тоді рівняння (1) можна записати у вигляді однорідної системи m лінійних алгебраїчних рівнянь з n невідомими. Кількість базисних невідомих системи дорівнює рангу r основної матриці системи, тобто матриці, складеної із координат векторів a1,a2…an. Таким чином, серед чисел існує r не рівних нулю. Згідно з означенням звідси випливає, що вектори a1,a2…an лінійно залежні. Для лінійно залежних векторів має місце рівність (1), з якої завжди можна один вектор виразити через лінійну комбінацію інших. Якщо вектори a1,a2…an із простору Еn (кожен з них має n координат) лінійно незалежні, тоді, тобто система n однорідних лінійних алгебраїчних рівнянь з n невідомими має тривіальний розв’язок. Але це можливо тоді, коли визначник матриці, складеної із координат векторів a1,a2…an, не дорівнює нулю. det= 2. Т1.Функція y=f(x) не може мати двох різних границь в одній точці. Т2.Якщо в деякому околі точки х0,крім, можливо самої точки х0,виконується нерівність f(x)≤ῳ(x) і кожна з функцій f(x) і φ(x) та має границю в точці х0,то T3.Нехай в деякому околі точки х0,крім, можливо самої точки х0, то виконується нерівність φ(x) ≤ f(x)≤ψ(х).Якщо функції φ(x) та ψ(х) мають границю в точці х0 при чому Т4.Якщо функція має в точці х0 границю тобто
3. Функція z одержить приріст Δхz = f (x+ Δx,y) – f (x; y), який називають частинним приростом по змінній х. Якщо приросту надати змінній у, то функція z одержить приріст ΔуZ = f (x+ Δx,y) – - f(x; y), який називають частинним приростом по змінній у. Якщо існує границя lim z=2x*lny+3(x^2)*(y^3)+3^x dz/dx=2*lny+6xy^3+ dz/dy=2x 4. Означення 1. Дріб називається раціональним, якщо його чисельник та знаменник є многочленами, тобто дріб має вигляд
де аі та bk — коефіцієнти многочленів, і = 0, 1,..., n; k = 0, 1, 2,..., m. Раціональний дріб називається правильним, якщо найвищий показник степеня чисельника n менше відповідного степеня m знаменника. Дріб називається неправильним, якщo Якщо
Означення 2. Найпростішими раціональними дробами І, II, III та IV типу називають правильні дроби вигляду: I. III. IV. Умова Розглянемо інтегрування найпростіших раціональних дробів. Інтеграли від найпростіших раціональних дробів 1-го та ІІ-го типів знаходять методом безпосереднього інтегрування: І. ІІ. При інтегруванні найпростішого дробу ІІІ-го типу треба спочатку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну. ІІІ.
Повертаючись до змінної х, та враховуючи, що
Інтеграл від найпростішого дробу типу IV шляхом повторного інтегрування частинами зводять до інтеграла під найпростішого дробу типу III.
5. Перш ніж обчислювати суму ряду, треба переконатись в його збіжності. Інакше можна витратити великі зусилля на пошук неіснуючої суми. Теорема про необхідну ознаку збіжності ряду. Якщо ряд збіжний, то його загальний член n a прямує до нуля при необмеженому зростанні n. Доведення. Припустимо, що ряд 1 2 3 a + a + a +K є збіжним. Тоді для нього справедлива рівність n n lim S S . Справедливою буде також і рівність n n 1 lim S S оскільки, коли n ®¥, то і (n - 1)®¥. Віднімемо від першої рівності другу: n n n n 1 lim S lim S 0 ®¥ ®¥ - - = або () n n n 1 lim S S 0 ®¥ - - =. Робимо остаточний висновок: оскільки n n1 n S S a - - =, то n n lim a 0 ®¥ =. Ознака порівняння. Нехай задано два знакододатні числові ряди:
та для всіх n виконується нерівність an <= bn. Тоді, якщо ряд (5) збіжний, то збіжний і ряд (4). Якщо ряд (4) розбіжний, то розбіжний і ряд (5). Порівняємо ряд
Білет №3 1. Визначники квадратних матриць. Способи обчислення визначників. Обчислити визначник двома способами:
Визначник – це число, що відповідає тільки квадратній матриці. Визначником другого порядку називають число, що дорівнює різниці добутків елементів головної та побічної діагоналей. Визначником третього порядку називають число, що обчислюється за правилами: Саррюса та трикутника. Визначником n-го порядку називають число, що дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпчика на відповідні їм алгебраїчні доповнення. Алгебраїчне доповнення Визначник можна обчислити двома способами: Саррюса(шляхом дописання 2-х перших рядків до матриці) та трикутника.
2. Кут між площинами. Умови паралельності і перпендикулярності двох площин.
Знайти кут між площинами
3. Похідна степенево – показникових функцій.
Знайти похідну функції
4. Обчислення наближеного значення функції в точці за допомогою повного диференціала.
Обчисліть за допомогою повного диференціала (1,04) 5. Диференціальні рівняння з відокремлюваннями змінними.
Знайти загальний розв’язок рівняння
Білет №16 1.Мішаний добуток, властивості мішаного добутку.
Знайти об’єм піраміди побудованої на векторних
2.Еквівалентні нескінченно малі величини. Ланцюжок еквівалентних нескінченно малих величин (при х → 0 і при х → х0
Обчислити границю:
2.Лінії рівня функції двох змінних.
Побудувати лінії рівня функції 2. Інтегрування тригонометричних функцій.
Знайти
3. Узагальнений гармонічний ряд та ряд геометричної прогресії.
Дослідити збіжність ряду
№23 23 1. Рівняння прямої з кутовим коефіцієнтом. Записати рівняння прямої з кутовим коефіцієнтом, якщо 2. Властивості функцій, неперервних на відрізку. Дослідити на неперервність функцію 3. Алгоритм дослідження функції на екстремум за допомогою першої похідної. Знайти екстремум функції 4. Метод інтегрування заміни змінної у визначеному інтегралі. Знайти визначений інтеграл 5. Абсолютна та умовна збіжність рядів. Дослідити збіжність Білет 17 1. Ве́кторний (ліні́йний) про́стір — основне поняття лінійної алгебри, узагальнення множини всіх векторів на площині чи в просторі з операціями додавання векторів та множення вектора на скаляр. Означення 8. Лінійно залежними називають вектори, якщо існує хоч би одне дійсне число (і = 1,2,…, n), що не дорівнює нулю і виконується рівність Означення 9. Лінійно незалежними називають вектори, якщо рівність (7) виконується тільки тоді, коли усі. В системі векторів a1,a2…an число лінійно незалежних векторів дорівнює рангу матриці, яка складена з координат цих векторів. Дійсно, якщо систему векторів a1,a2…an із простору Еm розглядати як матриці-стовпці з m заданими елементами, тоді рівняння (1) можна записати у вигляді однорідної системи m лінійних алгебраїчних рівнянь з n невідомими. Кількість базисних невідомих системи дорівнює рангу r основної матриці системи, тобто матриці, складеної із координат векторів a1,a2…an. Таким чином, серед чисел існує r не рівних нулю. Згідно з означенням звідси випливає, що вектори a1,a2…an лінійно залежні. Для лінійно залежних векторів має місце рівність (1), з якої завжди можна один вектор виразити через лінійну комбінацію інших. Якщо вектори a1,a2…an із простору Еn (кожен з них має n координат) лінійно незалежні, тоді, тобто система n однорідних лінійних алгебраїчних рівнянь з n невідомими має тривіальний розв’язок. Але це можливо тоді, коли визначник матриці, складеної із координат векторів a1,a2…an, не дорівнює нулю. det= 2. Т1.Функція y=f(x) не може мати двох різних границь в одній точці. Т2.Якщо в деякому околі точки х0,крім, можливо самої точки х0,виконується нерівність f(x)≤ῳ(x) і кожна з функцій f(x) і φ(x) та має границю в точці х0,то T3.Нехай в деякому околі точки х0,крім, можливо самої точки х0, то виконується нерівність φ(x) ≤ f(x)≤ψ(х).Якщо функції φ(x) та ψ(х) мають границю в точці х0 при чому Т4.Якщо функція має в точці х0 границю тобто
3. Функція z одержить приріст Δхz = f (x+ Δx,y) – f (x; y), який називають частинним приростом по змінній х. Якщо приросту надати змінній у, то функція z одержить приріст ΔуZ = f (x+ Δx,y) – - f(x; y), який називають частинним приростом по змінній у. Якщо існує границя lim z=2x*lny+3(x^2)*(y^3)+3^x dz/dx=2*lny+6xy^3+ dz/dy=2x 4. Означення 1. Дріб називається раціональним, якщо його чисельник та знаменник є многочленами, тобто дріб має вигляд
де аі та bk — коефіцієнти многочленів, і = 0, 1,..., n; k = 0, 1, 2,..., m. Раціональний дріб називається правильним, якщо найвищий показник степеня чисельника n менше відповідного степеня m знаменника. Дріб називається неправильним, якщo Якщо
Означення 2. Найпростішими раціональними дробами І, II, III та IV типу називають правильні дроби вигляду: I. III. IV. Умова Розглянемо інтегрування найпростіших раціональних дробів. Інтеграли від найпростіших раціональних дробів 1-го та ІІ-го типів знаходять методом безпосереднього інтегрування: І. ІІ. При інтегруванні найпростішого дробу ІІІ-го типу треба спочатку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну. ІІІ.
Повертаючись до змінної х, та враховуючи, що
Інтеграл від найпростішого дробу типу IV шляхом повторного інтегрування частинами зводять до інтеграла під найпростішого дробу типу III.
5. Перш ніж обчислювати суму ряду, треба переконатись в його збіжності. Інакше можна витратити великі зусилля на пошук неіснуючої суми. Теорема про необхідну ознаку збіжності ряду. Якщо ряд збіжний, то його загальний член n a прямує до нуля при необмеженому зростанні n. Доведення. Припустимо, що ряд 1 2 3 a + a + a +K є збіжним. Тоді для нього справедлива рівність n n lim S S . Справедливою буде також і рівність n n 1 lim S S оскільки, коли n ®¥, то і (n - 1)®¥. Віднімемо від першої рівності другу: n n n n 1 lim S lim S 0 ®¥ ®¥ - - = або () n n n 1 lim S S 0 ®¥ - - =. Робимо остаточний висновок: оскільки n n1 n S S a - - =, то n n lim a 0 ®¥ =. Ознака порівняння. Нехай задано два знакододатні числові ряди:
та для всіх n виконується нерівність an <= bn. Тоді, якщо ряд (5) збіжний, то збіжний і ряд (4). Якщо ряд (4) розбіжний, то розбіжний і ряд (5). Порівняємо ряд
Білет №3 1. Визначники квадратних матриць. Способи обчислення визначників. Обчислити визначник двома способами:
Визначник – це число, що відповідає тільки квадратній матриці. Визначником другого порядку називають число, що дорівнює різниці добутків елементів головної та побічної діагоналей. Визначником третього порядку називають число, що обчислюється за правилами: Саррюса та трикутника. Визначником n-го порядку називають число, що дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпчика на відповідні їм алгебраїчні доповнення. Алгебраїчне доповнення Визначник можна обчислити двома способами: Саррюса(шляхом дописання 2-х перших рядків до матриці) та трикутника.
2. Кут між площинами. Умови паралельності і перпендикулярності двох площин.
Знайти кут між площинами
3. Похідна степенево – показникових функцій.
Знайти похідну функції
4. Обчислення наближеного значення функції в точці за допомогою повного диференціала.
Обчисліть за допомогою повного диференціала (1,04) 5. Диференціальні рівняння з відокремлюваннями змінними.
Знайти загальний розв’язок рівняння
Білет №16 1.Мішаний добуток, властивості мішаного добутку.
Знайти об’єм піраміди побудованої на векторних
2.Еквівалентні нескінченно малі величини. Ланцюжок еквівалентних нескінченно малих величин (при х → 0 і при х → х0
Обчислити границю:
2.Лінії рівня функції двох змінних.
Побудувати лінії рівня функції 2. Інтегрування тригонометричних функцій.
Знайти
3. Узагальнений гармонічний ряд та ряд геометричної прогресії.
Дослідити збіжність ряду
№23 23 1. Рівняння прямої з кутовим коефіцієнтом. Записати рівняння прямої з кутовим коефіцієнтом, якщо 2. Властивості функцій, неперервних на відрізку. Дослідити на неперервність функцію 3. Алгоритм дослідження функції на екстремум за допомогою першої похідної. Знайти екстремум функції 4. Метод інтегрування заміни змінної у визначеному інтегралі. Знайти визначений інтеграл 5. Абсолютна та умовна збіжність рядів. Дослідити збіжність Рівняння прямої з кутовим коефіцієнтом. Кутовим коефіцієнтом прямої називається тангенс кута Рівняння прямої з кутовим коефіцієнтом має вигляд y = k * x + b, де k = tg
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 614; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 =8+1+45-10-6-6=32 det=0 вектори утворюють базис
=8+1+45-10-6-6=32 det=0 вектори утворюють базис ≤
≤ 
 =А то функція f(x) також має границю в цій точці і
=А то функція f(x) також має границю в цій точці і  =А.
=А. =1/0=∞
=1/0=∞ ,що не залежить від способу прямування
,що не залежить від способу прямування  , то її називають частинноюпохіднопершого порядку функції: u = f (
, то її називають частинноюпохіднопершого порядку функції: u = f (  ,
,  ,...,
,...,  ) по змінній
) по змінній  або
або 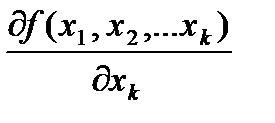 або u´
або u´  .
.


 .
. дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержати заданий дріб у вигляді суми многочлена та правильного раціонального дробу, тобто
дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержати заданий дріб у вигляді суми многочлена та правильного раціонального дробу, тобто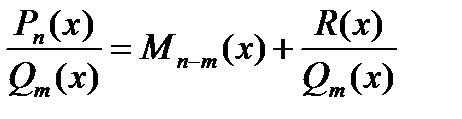
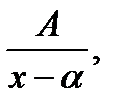 II.
II. 



 означає, що квадратний тричлен х2 + px + q не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен x2 + rx + s.
означає, що квадратний тричлен х2 + px + q не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен x2 + rx + s.





 або
або  одержимо:
одержимо:

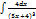 =4
=4  =
=  =4
=4  =4*
=4*  =
=  +C
+C



 =6/3+6/2*3^2+…+
=6/3+6/2*3^2+…+  … з еталонним рядом
… з еталонним рядом  =6/3+6/3^2+…+
=6/3+6/3^2+…+  ,
, , заданий ряд збігає
, заданий ряд збігає
 – це мінор зі знаком
– це мінор зі знаком  .
.  .
. - визначник, що залишився після викреслення і-го рядка та j-го стовпчика.
- визначник, що залишився після викреслення і-го рядка та j-го стовпчика.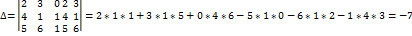


 та
та  .
.

 .
.

 (0,01)
(0,01)  .
.
 .
.



 , якщо
, якщо 
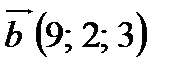
 . 39
. 39
 ).
).

 . 91
. 91
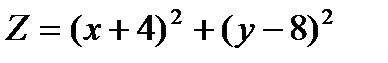 . 154
. 154 





 . 189
. 189


 . 242
. 242
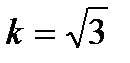 ,
,  .
. на відрізку
на відрізку  .
. .
. нахилу прямої до осі Ox, який відраховується в додатному напрямі (від осі до прямої проти годинникової стрілки). Цей кут завжди розглядається в межах від нуля до
нахилу прямої до осі Ox, який відраховується в додатному напрямі (від осі до прямої проти годинникової стрілки). Цей кут завжди розглядається в межах від нуля до  , тобто
, тобто  .
.



