
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютна та умовна збіжність рядів.Содержание книги
Поиск на нашем сайте
Знакозмінний ряд
називається абсолютно збіжним, якщо збігається знакододатний ряд
складений з абсолютних величин його членів. Якщо ряд (1) збіжний, а ряд (2) розбіжний, то ряд (1) називають умовно (не абсолютно) збіжним.
№26 1. Дії над матрицями. Властивості дій над матрицями. Знайти матрицю.
2. Означення похідної. Диференційовність та неперервність функції в точці і на проміжку.
Знайти похідну функції: 3. Правило Лопіталя.
Знайти границю, використавши правило Лопіталя 4. Невласний інтеграл з нескінченною верхнею межею.
5. Радіус, інтервал, область збіжності ряду.
№27 1. Визначники квадратних матриць. Способи обчислення визначників.
Обчислити визначник двома способами:. 2. Правила диференціювання сталої, суми, добутку, частки функцій, та наслідки з них.
Знайти похідну функції
3. Екстремум функції, необхідна та достатня умови існування екстремуму.
Знайти екстремум функції 4. Невласний інтеграл з нескінченною нижньою межею.
Знайти інтеграл 5. Ряд Тейлора.
Розкласти функцію РОЗВЯЗОК
№28 1. Визначник Квадратній матриці А n-го порядку можна поставити у відповідність число detА,яке називається визначником цієї матриці. Правило Лапласа:Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця)помноженні на відповідні алгебраїчні доповнення. Алгебраїчні доповнення Аij елемента aij називають мінор цього елемента,взятий із знаком «плюс»,якщо сума номерів рядка і стовпчика –число парне,та зі знаком «мінус»,якщо непарне.Мінором Мij елемента aij визначника n-го порядку називається визначник (n-1)-го порядку,який одержимо з даного визначника шляхом викреслювання і-го рядка та j-го стовпця,на пнрнтині яких знаходиться елемент aij.
Обчислити визначник використовуючи теорему Лапласа:
2. Похідна сталої та функцій Знайти похідну функ 3. Частинний приріст і частинні похідні першого порядку.
Знайти частинні похідні першого порядку функції
4. Відмінність між невласними інтегралами І та ІІ роду.7
Знайти інтеграл
5. Ряд Маклорена.
№7 1. Обернена матриця. Алгоритм оберненої матриці. Оберненою для заданої квадратної матриці А називається така матриця Будь-яка матриця, визначник якої не дорівнює 0, має обернену. Щоб знайти обернену матрицю до даної потрібно: 1. Знайти визначник даної матриці А, det A 2. Знайти алгебраїчні доповнення 3. Скласти приєднану матрицю 4. Знайти обернену матрицю за формулою
5. Якщо потрібно, то зробити перевірку, використовуючи означення
Знайти матрицю обернену до даної матриці А.
1. Знаходимо визначник матриці А: det A = 3*(-2)-1*2 = -8. 2. Знаходимо алгебраїчні доповнення:
3. Складаємо приєднану матрицю: А = 4. Обернена матриця 5. Перевірка:
2. Еліпс: означення, рівняння, графік, Еліпсом називається геометричне місце точок площини, для кожної із яких сума віддалей до двох заданих точок, що називаються фокусами, є величина стала. Якщо позначити через F1 і F2 точки, що є фокусами еліпса, а через М — будь-яку точку, що належить еліпсу, то еліпс характеризується тим,
Рис 1 що |MF1| + |MF2| = const. Введемо Декартові системи координат так, щоб фокуси F1,F2 були розташовані на осі Ох, симетрично відносно початку координат (рис. 1). І нехай М(х, у) — будь-яка (біжуча) точка, що належить еліпсу. Віддаль |F1F2| позначимо через 2с: |F1F2| = 2с, а через 2а — сталу, про яку йде мова в означенні, тобто |MF1| + |MF2| =2a Очевидно, що для існування еліпса повинно бути 2а > 2с, або а>с. Фокуси еліпса матимуть координати F1( — с, 0), F2(c, 0). відстані між двома точками дорівнюють яке називається канонічним рівнянням еліпса. 1. Знайдемо розташування кривої відносно координатних осей. Із (3) дістаємо 2.Еліпс розташований симетрично відносно координатних осей, тобто, якщо координати точки М1(х,у) задовольняють рівняння (3), то його задовольняють і координати точок М2( — х, у), М3 (— х, — у), M4(x, — у). Отже, еліпс має дві осі симетрії, розташовані на координатних осях. Точка перетину осей симетрії є центром симетрії і називається центром еліпса. Для еліпса, зображеного рівнянням (3), центром є початок координат О(0, 0). 1. Знайдемо точки перетину еліпса з координатними осями. Із (3) дістанемо: якщо х = 0, то у =± b, якщо y = 0, то х =± а. Отже, еліпс перетинає вісь Ох в точках А1( — а, 0), А2 (а, 0), а вісь Оу в точках В1 (0, —b), B2(0, b).
Рис 2 Точки А1, А2, B1, В2 перетину еліпса з його осями симетрії називаються вершинами еліпса (рис. 2). Відрізки А1А2 і B1B розташовані на осях симетрії. Вони називаються осями еліпса. Відрізок А1А2, довжина якого 2а — велика вісь, а В1В2 — довжина якого 2b — мала вісь (а> b). Відповідно числа а та b називаються великою і малою півосями еліпса. 4. Фокальною хордою еліпса називається хорда, що проходить через фокус перпендикулярно до його великої осі. Довжина фокальної хорди позначається через 2р. Знайдемо число р — фокальну пів хорду. Якщо Н1Н2 (рис. 2) фокальна хорда, то точки Н1 і Н2 лежать на еліпсі і їх координати задовольняють рівняння (3). Тому для точки Н2 (с, р) маємо
Отже, дістаємо Числа а, b,с,р є параметрами еліпса. 1. Ексцентриситетом еліпса називається число ε, що дорівнює відношенню фокальної півосі до великої півосі еліпса, і оскільки с<а. Величина ексцентриситету характеризує форму еліпса, його витягнутість по відношенню до осей. Перетворимо (4). Маємо Звідси випливає, що якщо а = b, то ε = 0, і еліпс перетворюється на коло. Якщо b значно менше, ніж а, то число ε близьке до 1 і еліпс витягнутий вздовж осі Ох. Аналогічно дістаємо, що |MF1| = а + εх. Тоді |MF1| + |MF2|=2a. Отже, рівняння (1) і (3) еквівалентні.
3. Правило Лопіталя. Пра́вило Лопіта́ля —— метод знаходження границь функції, розкриття невизначеностей вигляду Правило говорить, що якщо функції 1. 2. 3. 4. Якщо g(x) і f(x)— диференційовані в проколотому околі то існує Знайти границю за правилом Лопіталя 4. Невизначений інтеграл, основні властивості.
де F - первісна функції f (на проміжку); C - довільна стала. 1. 2. 3. Якщо
4. Знайти невизначений інтеграл для заданої функції f(x)=2x +
5. Диференціальні рівняння другого порядку, що дозволяють знизити порядок.
Знайти загальний розв’язок рівняння
№14 Теорыя::::!!!!!!!! 1. Розвязком СЛАР називається n значення невідомих х1=С1, х2=С2, х3=С3… хn=Сn при підстановці яких всі рівняння системи перетворюються в правильні рівності. Система рівнянь називається сумісною,якщо вона має хоча б один розв*язок,і несумісною,якщо вона не має жодного розвязку. Сумісна система називається визначеною,якщо вона має лише один розвязок,і невизначеною,якщо вона має безліч розв’язків.
Тут m - кількість рівнянь, а n - кількість невідомих. x1, x2,..., xn - невідомі, які треба визначити. a11, a12,..., amn - коефіцієнти системи - і b1, b2,... bm - вільні члени -передбачаються відомими. Індекси коефіцієнтів (aij) системи позначаютьномери рівняння (i) та невідомого (j), при якому стоїть цей коефіцієнт, відповідно. дорівнюють нулю (b1= b2 =... = bm = 0), інакше - неоднорідною. c 1(1) = c 1(2), c 2(1) = c 2(2), …, cn (1) = cn (2).
Сумісна система виду (1) називається визначеною, якщо вона має єдине рішення, якщо ж у неї є хоча б два різних рішення, то вона називається невизначеною. Якщорівнянь більше, ніж невідомих, вона називається перевизначенною.
Однорідна система лінійних рівнянь AX = 0 завжди сумісна. Вона має нетривіальні(ненульові) рішення, якщо r = rank A <n. Тоді n - r лінійно незалежними вектор-рішеннями будуть:
а будь-яке інше рішення є їх лінійною комбінацією. Вектор-рішення У лінійному просторі
2. (нескінченно велика функція). Функція називається нескінченно великою при x ® aабо в точці a, якщо для будь-якого позитивного числа e знайдеться таке позитивнеd (e), що для всіх x № a і задовольняють умові | xa | <d буде виконано нерівність | f(x) | > e. Аналогічно можна дати визначення нескінченно великою при
lim x ® ¥ f (x) = ¥ Û " e>0 $ d(e)>0 " x:|x|> d |f (x) |> e. 3. Функції декількох змінних Визначення. Якщо кожній парі (x, y) значень двох незалежних змінних з області Wставиться певне значення z, то говорять, що z є функція двох змінних (x, y). Dy z = f (x, y + Dy)-f (x, y) Dy z = x (y + Dy)-xy = xDy Dz = (x + Dx) (y + Dy)-xy = yDx + xDy + DyDx № Dy z + Dx z.
4. Метод невизначених коефіцієнтів. Будь-який неправильний раціональний дріь розкласти на суму найпростіших раціональних дробів типу 1-4, коефіцієнти яких можна знайти за допомогою методу невизначених коефіцієнтів. Інтегрування дробів методом невизначених коефіцієнтів проводиться за такою послідовністю: 1)Перетворити даний драб у правильний. 2)Перетворити знаменник у добуток найпростіших могочленів. 3)Записати правилиний дріб у вигляді суми найпростіших дробів 1-4 типів, де в чисельнику стоять невизначені коефіцієнти. 4)Звести суму найпростіших дробів до спільного знаменника і отримати СЛАР, прирівнявши коефіцієнти при однакових степенях змінної.. 5)Розвязок СЛАР дає невизначені коефіцієнти. 6)Кінцевий результат отримаємо післ обчислення інтегралів від многочлена і найпростіших дробів.
5. Властивості збіжних рядів. Якщо ряд (∞∑n=1) an збігається і має суму S, то ряд (∞∑n=1)C∙ an, одержаний множенням даного ряду на число C, також збігається і має суму C∙S. Якщо (∞∑n=1) an і (∞∑n=1) bn -два збіжних ряди відповідно з сумами S1 та S2, то ряд (∞∑n=1) (an + bn) також збігається і його сума дорівнює S1 + S2. Відкидання (приписування) скінченої кількості членів не впливає на збіжність ряду. Для того, щоб ряд (∞∑n=1) an збігався, необхідно і достатньо, щоб залишок ряду Rn прямував до нуля при n→∞, тобто lim(n→∞)Rn=0.
№15 Теория!!!!!!!!!!!!!!!!!!!!!!!!!!!!
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 987; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.28.97 (0.007 с.) |

 (1)
(1) (2)
(2)






 .
. Знайти інтеграл
Знайти інтеграл  .
.
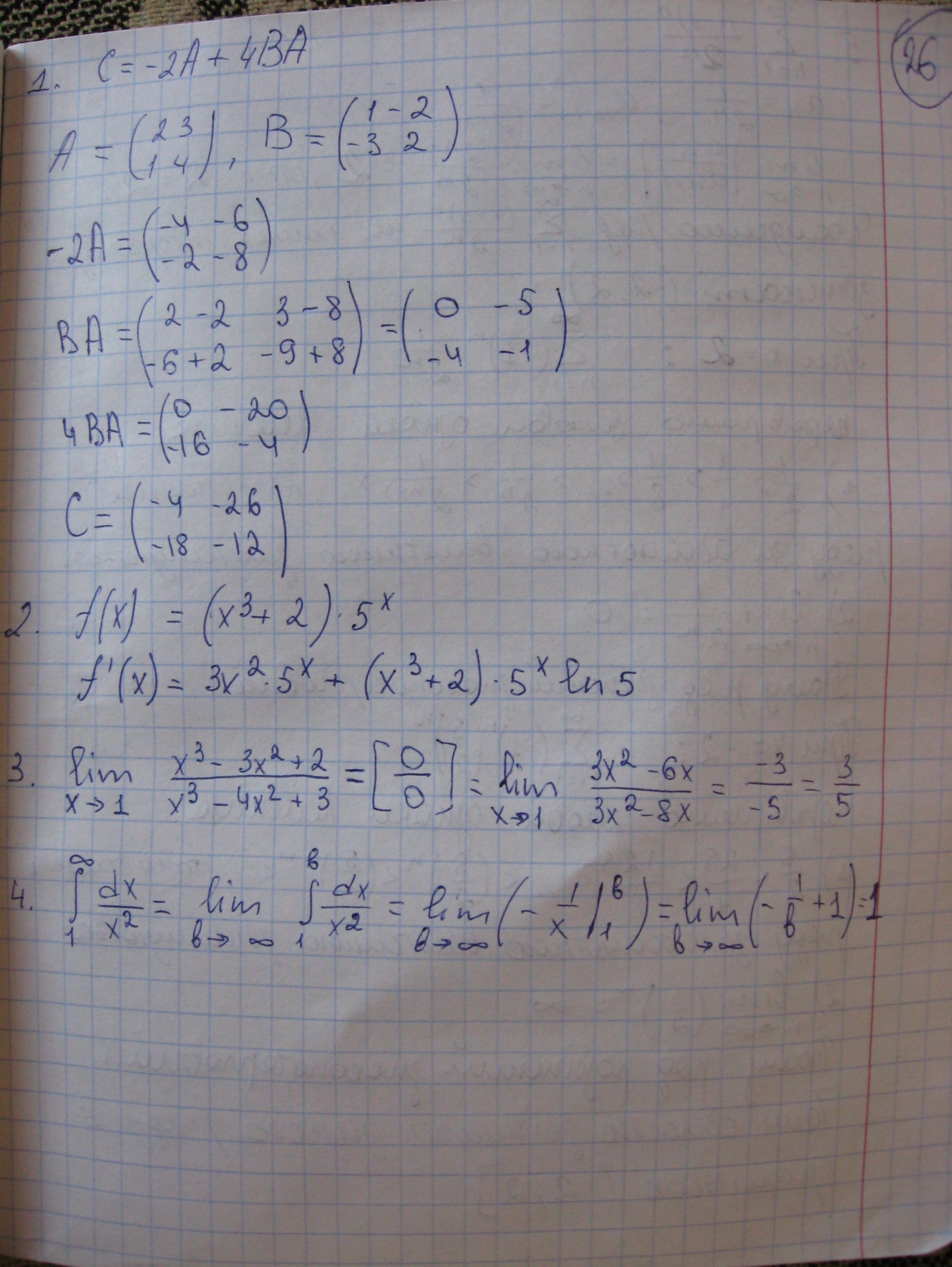




 .
.

 .
.


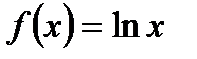 за степенями
за степенями 


 -го порядку. Теорема Лапласа.
-го порядку. Теорема Лапласа.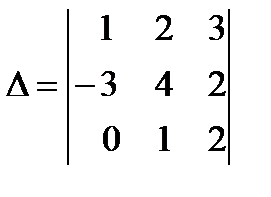

 (доведення). Таблиця похідних.
(доведення). Таблиця похідних.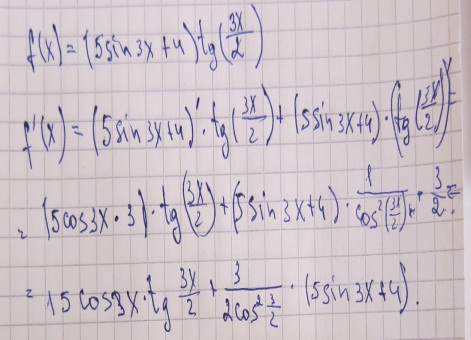


 .
.


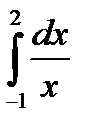

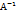 , добуток якої на матрицю А як зліва, так і справа дорівнює одиничній матриці, тобто А
, добуток якої на матрицю А як зліва, так і справа дорівнює одиничній матриці, тобто А  , де Е – одинична матриця такого порядку, що і матриця А. Матриця
, де Е – одинична матриця такого порядку, що і матриця А. Матриця  . Якщо det А=0, то матриця особлива, і до неї оберненої не існує.
. Якщо det А=0, то матриця особлива, і до неї оберненої не існує. елементів
елементів  матриці А.
матриці А. .
.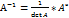 .
.

 = 2.
= 2. = -1.
= -1. = -2.
= -2. = 3.
= 3.
 =
= 
 =
= 
 = Е.
= Е.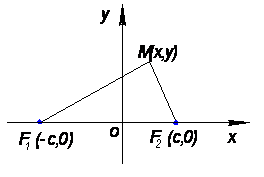

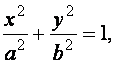 де b2=a2-c2 (3)
де b2=a2-c2 (3)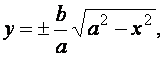 звідки | x | ≤ aбо x
звідки | x | ≤ aбо x 
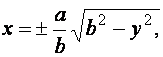 звідки | y | ≤ b або y
звідки | y | ≤ b або y 

 тобто
тобто 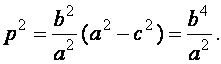

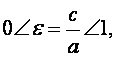 (4)
(4)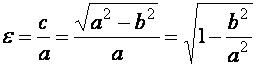

 і
і  . Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функції дорівнює границі частки їхніх похідних.
. Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функції дорівнює границі частки їхніх похідних. і
і 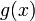 задовольняють такі умови:
задовольняють такі умови: або
або  ;
; ;
; в проколотому околі
в проколотому околі  ;
; . При цьому теорема вірна і для інших баз (для вказаної буде наведено доказ).
. При цьому теорема вірна і для інших баз (для вказаної буде наведено доказ).






 то
то
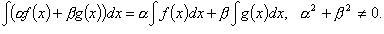
 – e
– e 
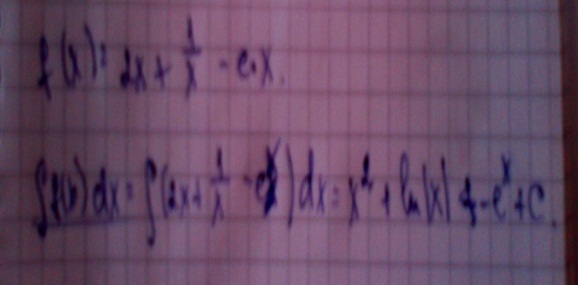







 утворюють нормовану фундаментальну систему.
утворюють нормовану фундаментальну систему.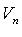 безліч рішень однорідної системи лінійних рівнянь утворює підпростір розмірності n - r;
безліч рішень однорідної системи лінійних рівнянь утворює підпростір розмірності n - r;  . Наведемо його у символічному запису:
. Наведемо його у символічному запису:


