
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координати і вектори на площині.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Метод координат – це спосіб визначення положення точки, фігури або тіла за допомогою чисел та інших символів, які наз. коор-ми. Підгот. робота до введ. коорд. площини поч. вже в 5 кл., де ввод. пон. " числовий промінь" і вказ., як зображ. на ньому натур. числа. У 6 кл. для зображ. дод. і ввід’ємних чисел ввод. числ. вісь, також пон. коорд-ти точки на прямій і на площ. ввод. описово на прикладах. Важливо щоб учні усвідомили, що коорд-та тч. на прямій це число, модуль якого = відстані точки прямої від початку відліка. Вся система вправ спрям. на формування умінь розв’язувати пряму і обернену задачі на визначення точки на коорд-ній прямій і пл.-ні. Вивч. у 8 класі даної теми треба поч. з повтор. і зведення в систему вже набутих знань і умінь. Ввод. означ. абсциси x і ординати y точки А (означ. ч-з термін "абсолютна величина числа")., поняття рівняння фігури в декартових координатах, кут коефіцієнта прямої. Вчит. повідомляє учням про те, що термін "декартові " пов’яз. з ім’ям Декарта, який вперше ввів їх до мат-ки. При введенні поняття рівняння фігури в декарт. коор-тах треба спир. на відомі з курсу алгебри 7 класу пон. р-ня з двома невідомими, лін. р-ня з 2-ма невід. 21 питання. Геометричні величини (довжини, кутові величини, площі, об’єми); методика їх вивчення у школі Геом. величини (довжина відрізка, величина (міра) кута, площа, об’єм) одночасно є і фіз. вел-ми. В учнів поступово пов. сформуватися уявлення про те, що вел-на - це заг. власт-сть певного класу об’єктів, їхніх станів або процесів, що в них відбуваються. З кількісного боку ця заг. власт. може бути індивідуальною для кожного об’єкта. Щодо вел. вживаються 3 терміни: 1) розмір величини, 2) значення величини, 3) числове знач. вел. Розмір вел. - кількісне вміщення тієї власт. даного об’єкта, яке відп. поняттю величина. Розмір вел. для даного об’єкта існує об’єктивно і не залежить від вибору одиниці вимірювання. Значення вел. - оцінка вел. у вигляді деякого числа прийнятих для неї одиниць (25 м, 2500 см). Числ. знач. вел. - це число, яке входить до знач. вел. (25 дм3 - знач. об’єму тіла, 25 - числ. знач. об’єму тіла). Перше уявлення про вел-ни і їх вимір. учні дістають ще в дошкіль. віці. Повтор. і розшир. відомостей про довжини відрізків і міру кутів та їх вимір. у 5-6 кл. доцільно спрям. на зв’язок з розв. текстових задач, перспективні зв’язки з наближеними обч-ми. Алгоритм (щоб вимір. вел-ну кута, треба): 1) накласти на кут транспортир так, щоб вершина кута збігалась з центром трансп., а одна сторона кута пройшла ч-з початок відліку на шкалі, 2) знайти штрих на шкалі, ч-з який пройде друга сторона кута, 3) визначити градус. міру кута, кор-сь цим штрихом і шкалою, ч-з поч. якої пройшла перша сторона кута. Аналог. можна сформулюв. алгоритм вимір. довжин відрізка лінійкою. При вимір. геом. вел-н треба поп-ньо вказати використ-ну одиницю вел-н, за д-гою якої буде записане отр. зн-ня вел-ни. Вивч-чи ф-лу довж. кола в 6 класі, варто зверн. увагу на те, що вимір. безпос. довж. цієї замкненої кривої лінії масштабною лінійкою, яка є відр. прямої, неможливо. Але можна знайти ф-лу, яка дає змогу обчислити довж. кола ч-з його радіус або діаметр, тобто ч-з відрізки прямої. При повтор. курсу геом. треба зверн. увагу учнів на те, що довж. відрізка і градус. міра кута - первісні пон., а аксіоми вимір. описують власт-ті цих понять. В тлумаченні геом. вел. здійснюється єдиний підхід: 1) рівні фігури мають рівні відповідні вел-ни (довжини, міри кута, об’єми), 2) якщо фігура розбив. на частини, то відповідна цій фігурі вел-на (довжина, міра кута, площа, об’єм) дорівнює сумі відп-х вел-н її частин, 3) існує одиниця вимір., тобто фігура, відповідна величина якої береться за одиницю (одиничний відрізок, центр. кут в 10, квадрат і куб, сторони яких є одиничним відрізком). Ч-з систему спец. підібраних задач корисно ознайомити учнів з ф-лами площ многок-ків (їх доцільно звести в окрему табл.). У курсі стереометрії 10-11 кл. розгл. вел.: кути, площі пов-хонь та об’єми многогранників. Вимір. кутів звод. до обчисл. плоских кутів (доц. розгл. вправи на побудову лін. кута даного двогран.). Обчисл. площ зводиться до обчисл. площ граней (многокутників), тому воно не становить труднощів (варто запроп. істор. довідку про Архімеда (квадратура круга, площі...)). Перші уявл. про об’єми учні отр. з 5 класу при вивч. паралелепіпеда. В 11 класі вони повертаються до вивчення об’ємів на дедуктивній основі (споч. ввод. пон. об’єму простих тіл по аналогії із площами). Формул-ся означ. об’єму простого тіла як дод. вел-ни, числ. знач. якої має три власт-ті. Далі довод. ф-ла об’єму прям. паралелепіпеда. 22.Методика вивчення тем "Паралельність прямих на площині". Сума кутів трикутника. Приступаючи до вивчення теми, доцільно виділити для учнів чотири блоки в змісті навчального матеріалу. 1) Паралельність прямих у просторі, мимобіжні прямі. 2) Парал-сть прямої і площини. 3) Парал-сть площин у просторі. 4) Парал. проектування як спосіб зображення просторових фігур на площині. Вивч. першого блоку навч. м-лу природно почати з розгляду можливих положень двох прямих а і b на площині і в просторі. В планіметрії: перетинаються, або паралельні. Далі, викор-чи стереометричний ящик, модель куба або прям-го парал-да, з’ясовують можливі положення двох прямих у просторі: перетинаються, лежать в одній площині і не перетинаються, не лежать в одній площині і не перетинаються. Як і в планіметрії, дві прямі в просторі вважаються такими, що перетинаються, якщо вони мають лише одну спільну точку. Після цього ввод. озн. парал-них і мимобіжних прямих у просторі. Озн. двох парал-них прямих у просторі включ. дві суттєві власт-ті: 1) лежати в одній площині, 2) не перетинатися. Кожна з цих власт-тей необхідна і лише обидві разом достатні для того, щоб дві прямі в просторі вважались парал-ними. Учні пов. добре усвід-ти озн. й ознаку парал. прямих, розуміти різницю між цими двома твердж-ми, дов. ознаку. Теорема про суму кутів трикутника є одним з фундаментальних тверджень, що стосується явластивостей трикутника. Навчальний матеріал цієї теми доповнює ознаки рівності три кутків важливим теоретичним матеріалом для розв’язування задач і доведення теорем. Основна мета – ознайомити учнів з теоремою про суму кутів трикутника і навчити дітей розв’язувати задачі із застосуванням даної теореми. У цій темі на рівні озн. вводяться нові поняття: внутрішні односторонні і внутрішні різносторонні кути,зовнішній кут трикутника, гіпотенуза і катети прямокутного трикутника. Вводити поняття внутрішні односторонніх і внутрішніх різносторонніх кутів краще наочно. Доводяться теореми в цій темі методом від супротивного, дітей залучають до самостійного пошуку доведення. наприклад:
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.011 с.) |

 (графік - пряма). Якщо пригад. Відоме з курсу алгебри 7 кл. пон. про систему 2-х лін. рівнянь з 2-ма невідомими, озн. розв’язку сист. і граф. спосіб її розв’яз., то учні самі дійдуть висновку щодо коорд-т точки пер-ну прямих. В курсі геометрії ставиться мета дов-ти, що рів-ня
(графік - пряма). Якщо пригад. Відоме з курсу алгебри 7 кл. пон. про систему 2-х лін. рівнянь з 2-ма невідомими, озн. розв’язку сист. і граф. спосіб її розв’яз., то учні самі дійдуть висновку щодо коорд-т точки пер-ну прямих. В курсі геометрії ставиться мета дов-ти, що рів-ня 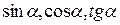 будь-якого кута від 0 до 1800 потребує мотивації. Однак споч. треба пригад. озн. синуса, косинуса і тангенса гострого кута ч-з віднош. сторін в прям-му трик-ку. В даній темі доводиться ряд тверджень: виведення формул коор-т сер. відрізка, довж відр., рівняння кола і прямої. Перед дов-ням ф-мул координат середини відрізка треба повтор. т-му Фалеса і спосіб визначення відстані між двома точками на прямій за їх коорд-ми, означ. модуля числа. Сист. задач теми спрям. на закріпл. введених понять викор. доведених ф-л. У 8-му кл. крім основних понять про вектори вивч-ся всі операції над векторами. В геом. вектором наз напрямлений відрізок. З метою мотив-ї учням слід нагадати що вони стикались з векторами в фізиці в 7кл.У темі, присв. векторам на площині, ввод. велика к-сть нових понять - абсол. вел-на, нуль. вектор, рівні вектори, коорд-ти, кут між ненуль. вект-ми, колінеарні... Коорд-ти вект., як і коорд. точки, дають можл. визнач. полож. вект. на коорд. площ., дають змогу означ. дії над вект., дов. їх власт-ті і застос. до розв’яз. задач. Учням проп. розгл. полож. 3-х вект. на коорд. площ. і порівн. їх розміщ. (помітити законом-сті)... Учні з допомогою системи вправ повинні виявити, що коор-ти рівних векторів однакові, а різних – різні. Учні визначають за допомогою ф-ли відстань між двома точками, довжану вектора а і роблять висновок, що lal= кореню квадратному із суми квадратів його координат. Суму і різницю вводять конкретно-індуктивним методом. Для векторного методу розв’яз. задач важливо, щоб учні навчились вільно шляхом відп-х побудов знах. Суму і різницю векторів (правило трик-ка і парал-ма). Скаляр. добуток ввод. ч-з коорд. векторів.
будь-якого кута від 0 до 1800 потребує мотивації. Однак споч. треба пригад. озн. синуса, косинуса і тангенса гострого кута ч-з віднош. сторін в прям-му трик-ку. В даній темі доводиться ряд тверджень: виведення формул коор-т сер. відрізка, довж відр., рівняння кола і прямої. Перед дов-ням ф-мул координат середини відрізка треба повтор. т-му Фалеса і спосіб визначення відстані між двома точками на прямій за їх коорд-ми, означ. модуля числа. Сист. задач теми спрям. на закріпл. введених понять викор. доведених ф-л. У 8-му кл. крім основних понять про вектори вивч-ся всі операції над векторами. В геом. вектором наз напрямлений відрізок. З метою мотив-ї учням слід нагадати що вони стикались з векторами в фізиці в 7кл.У темі, присв. векторам на площині, ввод. велика к-сть нових понять - абсол. вел-на, нуль. вектор, рівні вектори, коорд-ти, кут між ненуль. вект-ми, колінеарні... Коорд-ти вект., як і коорд. точки, дають можл. визнач. полож. вект. на коорд. площ., дають змогу означ. дії над вект., дов. їх власт-ті і застос. до розв’яз. задач. Учням проп. розгл. полож. 3-х вект. на коорд. площ. і порівн. їх розміщ. (помітити законом-сті)... Учні з допомогою системи вправ повинні виявити, що коор-ти рівних векторів однакові, а різних – різні. Учні визначають за допомогою ф-ли відстань між двома точками, довжану вектора а і роблять висновок, що lal= кореню квадратному із суми квадратів його координат. Суму і різницю вводять конкретно-індуктивним методом. Для векторного методу розв’яз. задач важливо, щоб учні навчились вільно шляхом відп-х побудов знах. Суму і різницю векторів (правило трик-ка і парал-ма). Скаляр. добуток ввод. ч-з коорд. векторів.


