Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поелементні операції з векторамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте У попередніх розділах вектор використовувався як аргумент математичних функцій, результатом яких був вектор з елементами, рівними значенням функції від відповідних елементів початкового вектора. Таким чином, відбувалося поелементне обчислення функції, що викликалася. У цьому розділі детально описані можливості поелементної роботи з векторами, які знадобляться надалі, зокрема, для визначення власних функцій і побудови їх графіків. Введіть два вектор-рядки:
Операція.* (не вставляєте пропуск між точкою і зірочкою!) призводить до поелементного множення векторів однакової довжини. В результаті виходить вектор з елементами, рівними твору відповідних елементів початкових векторів:
За допомогою.^ здійснюється поелементне піднесення до ступеня:
Показником cтепеня може бути вектор тієї ж довжини, що і що підноситься до степеня. При цьому кожен елемент першого вектора підноситься до ступеня, рівного відповідному елементу другого вектора:
Ділення відповідних елементів векторів однакової довжини виконується з використанням./
Зворотне поелементне ділення (ділення елементів другого вектора на відповідні елементи першого) здійснюється при допомозі.\
Отже, точка в MATLAB використовується не лише для введення десяткових дробів, але і для вказівки того, що ділення або множення масивів однакового розміру має бути виконане поелементно. До поелементних відносяться і операції з вектором і числом. Складання вектора і числа не призводить до повідомлення про помилку. MATLAB додає число до кожного елементу вектора. Те ж саме справедливе і для віднімання:
Множити вектор на число можна як справа, так і ліворуч:
Ділити за допомогою знаку / можна вектор на число:
Спроба ділення числа на вектор-рядок призводить до повідомлення про помилку:
Якщо вимагається розділити число на кожен елемент вектора і записати результат в новий вектор, то слід використовувати операцію./.
Усі вищеописані операції застосовані як до вектор-рядків, так і до вектор-столбцам. Розберемо, як правильно транспонувати і обчислювати зв'язані вектори в MATLAB. Для вектор-столбця, приміром з трьома комплексними елементами (зокрема і з речовими), зв'язаний до нього і* визначається як вектор-рядок з його комплексно-зв'язаних елементів, а транспонований иТ - просто як вектор-рядок з його елементів, наприклад:
Аналогічно визначається сполучення (сопряжение) і транспонування для векторстроки, що призводить до вектор-столбцу. Ясно, що для векторів, що складаються тільки з дійсних чисел, операції сполучення (сопряжение) і транспонування співпадають. Для знаходження зв'язаного вектора в MATLAB використовується апостроф, а для транспонування слід застосовувати точку з апострофом:
Операції.’ і ’ над векторами приведуть до однакових результатів. Множення векторів Вектор можна помножити на інший вектор скалярний (цей твір ще називають внутрішнім), векторний, або утворити так званий зовнішній твір. Результатом скалярного твору є число, векторного - вектор, а зовнішнього - матриця. Скалярний добуток Скалярний добуток векторів а і b довжини N, що складаються з дійсних чисел, визначається формулою
Отже, для обчислення скалярного добутку необхідно підсумувати компоненти вектора, отриманого в результаті поелементного множення a на b, тобто потрібно використовувати функцію sum і поелементне множення. Нижче приведена необхідна послідовність команд:
Скалярний добуток векторів можна також вичислити, застосувавши функцію MATLAB dot >> s = dot(a,b); Знайдіть довжину (модуль) вектора а Рішення:
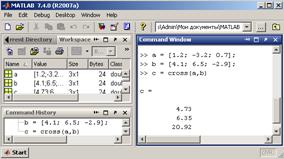
Векторний добуток Векторний добуток a × b визначено тілько для векторів із тривимірного простору, тобто, який складається із трьох елементів. Результатом є вектор із тривимірного простору. Для обчислення векторного добутку в MATLAB служит функция cross:
Обрахуємо a × b + b × a. Якщо отримаємо вектор, який складається з нулів, то ви все проробили вірно, так як для любих векторів виконується властивість a × b= − b × a. Змішанний добуток векторів а, b, с визначається по формулі abc = а∙(b ×с). Модуль змішанного добутку векторов дорівнює об’єму паралелепипеда, побудованого на цих векторах. Знайдіть об’єм паралелепіпеда. Правильність дій:
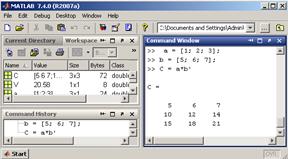
Зовнішній добуток Вектор-стовпчик в MATLAB задається у вигляді двовимірного масиву размера N на один. Вектор-стовпчик b при транспонуванні переходить в вектор-рядок разміру один на М. Вектор-стовпчик і вектор-рядок є матриця, у якій один із размірів дорівнює одиниці. Фактично С = abT, де множення відбувається за правилом матричного добудку. Для обрахунку матричного добутку в MATLAB використовується оператор "зірочка":
MATLAB вивела в командне вікно матрицу в загальному виді — по рядкам. Використовуючи команду whos для перегляду змінних робочого середовіща або вікно Workspase. Числа, вектори і матриці зберігаються в двовимірних масивах числа - в масивах, размірністью один на один, вектор-стовчкики і вектор-рядки містят в масивах, у яких один із розмірів рівний одиниці, а для матриц виділяються двовимерні масиви. Тому операції і вбудовані функції в MATLAB використовуються у вигляді аргументів, видаючи результат у відповідному вигляді. Двумерные массивы, матрицы В этом разделе описан ввод матриц, математические операции с ними, поэлементные операции, вычисление функций от элементов матриц, чтение и запись с использованием текстового файла, простейшая визуализация матричных данных.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.216 (0.01 с.) |




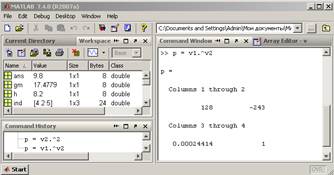




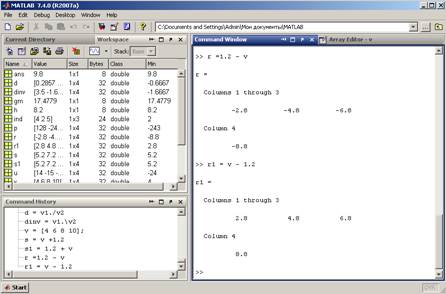




 ,
,  ,
,