Введення матриць, прості операції

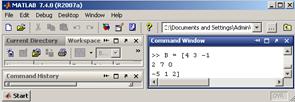
Різні способи введення

Вводити невеликі за розміром матриці зручно прямо з командного рядка. Введіть матрицю розмірністю два на три.

Для зберігання матриці використовуйте двовимірний масив з ім’ям А. При введенні врахуйте, що матрицю А можна розглядати як вектор-стовпець з двох елементів, кожен з яких є вектор-рядком довжиною три, отже, рядки при наборі відокремлюються крапкою з комою:

Для вивчення найпростіших операцій над матрицями нам знадобиться ще кілька матриць. Розглянемо інші способи введення. Введіть квадратну матрицю розміру три так, як описано нижче:

Почніть набирати в командному рядку

Нажмите клавишу <Enter>. Обратите внимание, что MATLAB ничего не вычислила. Курсор мигает на следующей строке без символа >>. Продолжите ввод матрицы построчно, нажимая в конце каждой строки <Enter>. Последнюю строку завершите закрывающей квадратной скобкой, получается:

Натисніть клавішу <Enter>. Зверніть увагу, що MATLAB нічого не обрахувала. Курсор блимає на наступному рядку без символу >>. Продовжіть введення матриці порядково, натискаючи в кінці кожного рядка <Enter>. Останній рядок завершіть закриваючою квадратної дужкою, виходить:

Ще один спосіб введення матриць полягає в тому, що матрицю можна трактувати як вектор-рядок, кожен елемент якої є вектор-стовпцем.

Наприклад, матрицю два на три можна ввести за допомогою команди:

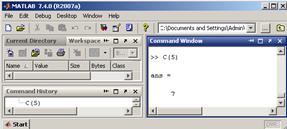
Подивіться змінні робочого середовища у вікні Workspace або наберіть у командному рядку whos. Отже, в робочому середовищі міститься три матриці, дві прямокутні і одна квадратна.

Доступ до елементів матриць

Доступ до елементів матриць здійснюється за допомогою двох індексів - номерів рядка і стовпця, укладених в круглі дужки, наприклад

Звернення до елементів матриць

Елементи матриць можуть входити до складу виразів:

Розташування елементів матриці в пам’яті комп’ютера визначає ще один спосіб звернення до них. MATLAB зберігає елементи матриці в пам’яті по стовпцях. Елементи q_ij матриці Q розміру m на n містяться в пам’яті в послідовності:

q₁₁, q₂₁,.., q_m1, q₁₂, q₂₂,.., q_m2,.., q_1n, q_2n,.., q_mn,

Отже, для доступу до елементів матриці можна використовувати один індекс, задаючий порядковий номер елемента матриці в векторі. Наприклад, елементи матриці С,, записані в такому порядку

С (1, 1), С (2, 1), С (1, 2), С (2, 2), С (1, 3), С (2, 3)

Тому звернення до елементів матриці як до елементів вектора за допомогою одного індексу (індексація за допомогою порядкового номера) призводить до передбачуваному результату але може послужити і джерелом помилок в обчисленнях, якщо один індекс випадково зазначений замість двох - ніякого попередження не виводиться

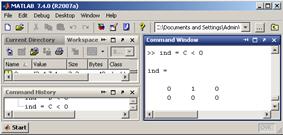
Як правило, часто краще використовувати два індекси, за винятком деяких спеціальних випадків, наприклад, проходу елементів матриці по стовпцях.

Ще одним способом звернення відразу до всіх елементів матриці, що задовольняє деякому умові, є логічне індексування. Логічне індексування не є необхідним для виконання звичайних операцій матричної алгебри, тому при першому читанні наступний розділ можна пропустити. Однак воно істотно розширює можливості обробки векторних і матричних даних, дозволяючи наочно і компактно записувати вирази з досить складною логікою без програмування перебору даних

Логічне індексування

Логічне індексування (logical subscripting) дозволяє вибрати з масиву елементи, що задовольняють певним умовам, які задані логічним вираженням. Нехай з введеної вище матриці C потрібно вибрати всі негативні елементи і записати їх у вектор f. Спочатку виконаємо, здавалося б, неприпустиму дію: запишемо в змінну ind результат порівняння матриці і числа нуль.

Утворився логічний масив (logical array) ind того ж розміру, що і в (див. вікно Workspace), що складається з нулів і одиниць, причому одиниці відповідають негативних елементів масиву C. Вказівка ​​логічного масиву ind в якості єдиного індексу вихідного масиву в дозволяє вирішити поставлене завдання:

Зрозуміло, можна було обійтися і без допоміжного масиву ind, написавши відразу f = C (C <0).

Якщо потрібно привласнити нове значення елементів масиву, що задовольняє певній умові, то вираз C (C <0) повинно увійти в ліву частину оператора привласнення.

Тільки що ми розглянули новий тип даних MATLAB - логічні масиви. У нашому прикладі логічний масив ind був автоматично створений при виконанні операції порівняння C> 0. Було б помилкою вважати, що для виділення потрібних елементів досить просто створити масив з нулів і одиниць і вказати його в якості індексу масиву. Введіть, наприклад, з командного рядка масив indi з тими ж елементами, що і ind:

>> ind1 = [0 0 1; 0 0 0; 10 0];

і спробуйте використовувати його для логічного індексування, виходить помилка:

>> В(indl)

??? Subscript indices must either be real positive integers or

logicals.

Вихід полягає в перетворенні числового масиву indl в логічний масив ind2 за допомогою функції logical, який потім застосовується для індексування:

>> ind2 = logical(indl);

Переконайтеся, що ind2 - логічний масив, вивчивши інформацію про нього у вікні Workspace. Логічне індексування векторів створюється аналогічно.

Логічне індексування дозволяє отримати значення потрібних елементів матриці або вектора або змінити їх, але індекси елементів залишаються невідомими. Для пошуку індексів елементів, що задовольняють певній умові, служить функція find. Ось простий приклад: потрібно знайти номери всіх елементів вектора, рівних максимальному значенню.

Виклик функції mах з двома вихідними аргументами не вирішує цю задачу, оскільки знаходиться тільки один елемент і його номер:

Тепер ми знаємо значення m максимального елемента, воно дорівнює 5, і могли б використовувати логічне індексування для запису всіх максимальних значень в вектор. Подвійний знак == позначає логічне рівність:

але номери максимальних елементів все одно невідомі. Замість логічного індексування використовуємо функцію find, вказавши у вхідному її аргументі логічне вираження х == 5

Функція find повернула номери елементів вектора, співпадаючих з максимальним значенням.

Аналогічний пошук в матриці так само здійснюється за допомогою find.

Нехай, наприклад, треба знайти індекси всіх непозитивно елементів матриці В, введеної вище. Викличемо find з двома вихідними аргументами - векторами, в які потрібно записати значення рядкових і столбцевих індексів шуканих елементів матриці

Дійсно, всі ці елементи b₃₁, b₁₃ і b₂₃ менше або дорівнюють нулю.

У цьому прикладі до функції find можна звернутися і з одним вихідним аргументом:

У цьому випадку вектор k містить номери необхідних елементів матриці з урахуванням описаної вище схеми зберігання в пам’яті по стовпцях.

Звернемося тепер до основних операцій з матрицями в MATLAB.