Застосування функцій обробки даних до матриць

Функція sum обчислює суму елементів вектора. З іншого боку, вектори в MATLAB, так само як і матриці, зберігаються в двовимірних масивах. Виникає питання: що ж буде, якщо в якості аргументу sum використовувати не вектор, а матрицю. Виявляється, MATLAB обчислить вектор-рядок, довжина якої дорівнює числу стовпців матриці, а кожен елемент є сумою відповідного стовпця матриці, наприклад:

Функція sum за замовчуванням обчислює суму по стовпцях, змінюючи перший індекс масиву при фіксованому другому. Для того щоб виробляти підсумовування по рядках, необхідно викликати sum з двома аргументами, вказавши місце індексу, за яким слід підсумовувати

Зауважте, що sum (M) і sum (M, l) призводять до однакових результатів.

Отже, функція sum підсумовує або по рядках, або по стовпцях, видаючи результат у вигляді вектора або вектор-рядка. Аналогічно працює і функція prod:

Функція sort впорядковує елементи кожного з стовпців матриці в порядку зростання. Виклик sort з другим аргументом, рівним двом, призводить до впорядкування елементів рядків:

Так само як і для векторів, функція sort дозволяє отримати матрицю індексів відповідності елементів вихідної і впорядкованої матриць. Для цього необхідно викликати sort з двома вихідними аргументами:

Матриці М, МС і.Ind пов’язані між собою так: МС (i, j) = М (ind (i, j), j), де i та j змінюються від одного до трьох.

Функції max і min обчислюють вектор-рядок, що містить максимальні чи мінімальні елементи у відповідних стовпцях матриці:

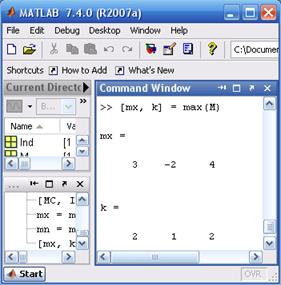
Для того щоб дізнатися не тільки значення максимальних або мінімальних елементів, але і їх номери в стовпцях, слід викликати max або min так:

Зверніть увагу, що у другому стовпці матриці М два рівних максимальних елемента-перший і третій. Завжди повертається номер першого максимального елемента (другий елемент у вектор-рядку дорівнює одиниці).

Точно так само працює і min у випадку двох рівних мінімальних елементів в стовпці матриці. Функції max і min дозволяють виділити максимальні чи мінімальні елементи з двох матриць однакових розмірів і записати результат в нову матрицю того ж розміру, що і вихідні:

Одним з аргументів може бути число. У результуючу матрицю записується максимум з цього числа і відповідного елемента вихідної матриці:

Якщо обидва аргументи функцій min або mах є числами, то повертається мінімальне або максимальне з цих чисел.

Для знаходження максимуму або мінімуму не по стовпцях матриці, а по рядках, передбачена наступна форма виклику з другим аргументом - порожнім масивом

Для того щоб додатково отримати номера максимальних елементів в рядках, використовуємо виклик mах з двома вихідними аргументами:

Розглянемо функцію rot90, повертаючи масив на 90 градусів проти годинникової стрілки. Застосуйте цю функцію до згадуваного масиву Р:

Застосуйте функцію повторно, але вже до масиву q1.

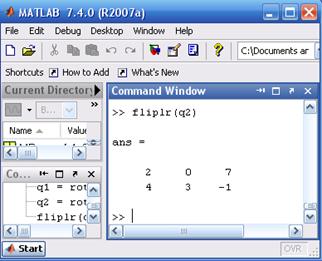
Функция fliplr забезпечуєт дзеркальне відображення від умовної вертикалі, яка проходить через середину масива:

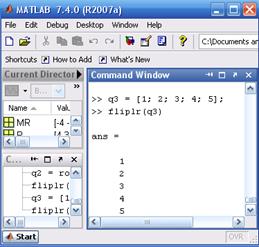
Зверніть увагу на те, що вектор-стовпець не змінюється під впливом функції fliplr:

Приклад:

Функція magic (n) задає магічну матрицю розміру пхп, у якої сума всіх стовпців, всіх рядків і навіть діагоналей дорівнює одному й тому ж числу:

Вже сама по собі можливість створення такої матриці за допомогою простої функції magic зацікавить любителів математики. Але векторних і матричних функцій у системі безліч, і ми їх детально розглянемо в подальшому.

Для стирання змінних з робочої області пам'яті служить команда clear.

Видалення стовпців і рядків матриць

Для формування матриць і виконання ряду матричних операцій виникає необхідність видалення окремих стовпців і рядків матриці. Для цього використовуються порожні квадратні дужки []. Проробимо це з матрицею N:

Видалимо другий стовпець використовуючи оператор: (двокрапка) матрицею N:

А теперь, використаємо оператор: (двокрапка), видалимо другий рядок: