
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язування задач на побудову . Основні методи .Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Найпростіші геом. побудови учні викон. уже в поч. школі та в 5-6 класах: проводять прямі, кола, відрізки, рівні даним, будують кути заданої градусної міри, викор-чи транспортир... У курсі геом. спец. виділяються задачі на побудову, які розв’язуються лише за допомогою циркуля і лінійки. Вони мають значну дидактичну цінність, бо не лише формують практичні навички виконання осн. побудов, а й розвивають лог. мислення, формують евристичну діяльність. Такі задачі розв. в 4 етапи: 1) аналіз задачі, 2) побудова за знайденим планом, 3) доведення, 4) дослідження. Осн. мета вивч. геом. побудов у школі - навчити учнів виконувати основні побудови циркулем і лінійкою та розв’язувати нескладні комбіновані задачі, які зводяться до виконання осн. побудов. До осн. побудов віднесено 5 побудов: 1) трикутника за даними сторонами, 2) кута, що дорівнює даному, 3) бісектриси даного кута, 4) перпендикулярної прямої, 5) поділ відрізка пополам. Лінійкою можна лише провести: 1) довільну пряму, 2) довільну пряму, що проходить через дану точку, 3) пряму, що проходить через дві дані точки. Циркулем можна лише описати коло з даного центра даним радіусом, зокрема відкласти на даній прямій від даної точки даний відрізок. Треба вимагати від кожного учня засвоєння алгоритму основної побудови. Напр., щоб побудувати бісектрису кута, треба: 1) описати з вершини кута як із центра коло довільного радіуса, 2) з точок перетину побудованого кола зі сторонами кута описати два кола тим самим радіусом і позначити їх точку перетину, відмінну від вершини кута, 3) через вершину кута і точку перетину кіл провести промінь, який є бісектрисою кута Основні методи розв’язування задач на побудову: 1. метод ГМТ; 2. метод симетрії; 3. метод ПП; 4. алгебраїчний. Метод ГМТ. Види ГМТ: 1) ГМТ рівновіддалених на дану відстань а, від даної точки О є коло з радіусом а і з центром в т. О. 2) ГМТ рівновіддалених від сторін даного кута є бісектриса цього кута. 3) ГМТ рівновіддалених від вершин даного трикутника є центр кола описаного навколо трикутника,в ГМТ рівновіддалених сторін даного трикутника є центр вписаного трикутника. 4) ГМТ які лежать від даної прямої а, на відстані а є дві паралельні прямі. Суть розв’язання задач на побудову методом ГМТ:
- з умов поданих в задачах беруть лише одну, відкидаючи решту. Цим самим задача стає невизначеною, тобто такою, яка має безліч розв’ясків. - побудувавши необхідне ГМТ розглядають іншу умову задачі і будують ще одне ГМТ іт.д. - спільні точки, які належать всим ГМТ побудовані за умовою задачі ідають остаточний результат,шукану фігуру або лінію. Метод симетрії: Перетворення фігури В у фігуру В2 при якому кожна її точка Х переходить в т. Х1 симетричну відносно даної т.О, наз. перетворенням симетрії відносно т. О. При цьому фігури В іВ1 наз. симетричними відносно т.О.відносно т.О. Слід звернути увагу учнів на те: -положення прямої (відрізка) задається двома точками; -положення кола задається центром і будь-якою точкою; -положення трикутника задається положенням його вершини. Важливо виділити достатні умови при яких задається центральна і осьова симетрії. Щоб задати центральну симетрію достатньо вказати: центр або дві відповідні точки. Для осьової симетрії аналогічно. Метод паралельного перенесення: Метод паралельного перенесення є найбільш доцільним, коли безпосередня побудова шуканої фігури складае певні труднощі в зв’яску з віддаленістю її елементів. Віддаленість елементів може позначатися не тільки на віддаленість їх одна від одної але і направленості компонування цих елементів. Тоді елементи фігури переносяться паралельно самим собі на таку відстань, щоб одержану фігуру, після перенесення, можна було побудувати більш просто ніж шукану. Після побудови допоміжної фігури, зворотнім паралельним перенесенням отримують шукану фігуру. Алгебраїчний метод: - коли шукана геометрична величина обчислюється на основі різних залежностей між елементами різниг геометричних фігур безпосередньо або за допомогою рівнянь. Розв’язування задач на побудову (алгебр. Методом), зводиться до етапів: -складання рівнянь до умови задачі; -розв’язання одержаного р-ня відносно букви, яка позначае шуканий відрізок; - дослідження отриманою формою; - побудова відрізка за складенною формулою. математики доцільно ознайомити учнів із загальними методами побудови перерізів тіл, зокрема многогранників. Мається на увазі метод внутрішнього проектування (метод відповідності) і метод слідів при паралельному і центральному проектуванні
17 Геометричні перетворення у шкільному курсі математики.Рух Геом. пер-ня, зокрема, рухи, розглядались в геом. ще за часів Евкліда, хоча в різні часи розвитку мат-ки і шкільного курсу їм приділялась неоднакова увага. Осн. мета вивчення геом. пер-нь - ознайомити учнів з різними видами рухів (осьова і центральа симетрія, поворот, паралельне перенесення) та подібністю і гомотетією (подібність є в окремій шпаргалці), їх власт-ми, ввести заг. поняття про рівність і подібність фігур, показати застос. окремих видів пер-нь, ознак подібності трик-ків до розв’яз-ня задач. У підр. Погорєлова пон. перетворення фігури ввод. на наочному, інтуїтивному рівні, пон. руху ввод. на рівні озн.: пер-ня однієї фігури в іншу наз. рухом, якщо воно зберігає відстань між точками, тобто переводить будь-які дві точки X і Y однієї фігури в точки X’ і Y’ іншої фігури так, що XY=X’Y’. Тут доцільно скористатися рухомими планіметричними моделями. У підр. Погорєлова викор. конструктивні озн., вводячи пон. центрально-симетричних і симетричних відносоно даної прямої точок. Озн. фігури, симетричної відносно даної точки і центр.-сим. Фігури, не виклик. труднощів, якщо проілюструвати такі фігури різноманітними прикладами. Аналог. ввод. пон. точок, сим-них відносно прямої l. При введенні пон. фігури, сим-ної відносно даної точки і даної прямої, важливо, щоб учні навчились будувати точку, відрізок, пряму, трикутник..., симетричні відп-ним фігурам відносно точки і відносно прямої. Важливо виділити достатні умови, при яких задається центральна і осьова симетрії. Щоб задати центральну (осьову) симетрію, досить указати: 1) центр (вісь) симетрії або 2) дві відповідні точки. У другому вип. неважко побуд. центр і вісь симетрії. При введенні поняття повороту варто підкреслити, що будь-який поворот може бути заданий: 1) центом О, кутом повороту
18. Методика введеня теми „перетворення подібності”. Дана тема, у складі якої вивчається перетворення подібності, має не лише теоретичне, а практичне значення (фото-, кіносправа, архітектура, машинобудування, картографія...). Подібність вивч. у 9 класі, а не разом з рухами. Провідними поняттями теми є пон. пер-ня под-сті і гомотетії, подібних фігур. Найважчими з погляду сприймання учнями і методики вивч. є пон. пер-ня подібності. Розпочати можна з введення терміна "подібні фігури", т.я. з ним учні неодноразово стикалися у життєвій практиці. Спир-сь на ці уявл. і розглянуті в класі приклади, учні можуть сам. сформулюв. озн. пер-ня подібності. Доц. споч. пригадати вже відоме учням озн. одного з пер-нь (руху) і ще раз звернути увагу на те, що при цьому пер-ні зберіг. відстань між двома точками даної фігури і відповідними точками фігурами, одержаної внаслідок перетворення. За готовими малюнками розглядаються властивості, озн., вводиться поняття про коефіцієнт подібності к (при к=1 - рух). Корисно поставити перед учнями завдання сформулюв. озн. подібних фігур за аналогією з означенням рівних фігур. Природно зразу ж ввести озн. подібних фігур як таких, що переводяться одна в одну пер-ням подібності. Заг. озн. под-х фігур дає можл-сть не формулювати окремо озн. подібних трик-ків. Доц. наголосити, що будь-які два кола подібні, і запроп. учням навести ще приклади. Слід зверн. увагу учнів на те, що кожні дві гомотетичні фігури подібні, але не кожні дві подібні фігури гомотетичні. Варто запроп. учням виконати пер-ня гомотетії трик-ка, кола, квадрата. Поняття вписаного і центрального кутів вводять або конкретно-індуктивним або абстрактно-дедуктивним методом. Озн. плоского кута пов. ввести сам учитель. У підр. Погорєлова вивч. дов. п’яти теорем, з яких важливіші ті, які стосуються ознаки подібності трикутників і вимірювання вписаного кута. Крім того, дов-ся деякі твердження, які не названо т-мами, а саме: власт-сть пер-ня подібності і її наслідки, власт-ть транзитивності відношення подібності фігур, співвіднош. елементів прямокутних трикутників і власт. бісектриси трикутника ділити протилежну сторону на частини, пропорційні двом іншим сторонам. Після вивч. власт-ті пер-ня подібності і власт-тей подібних фігур, що випливають з неї, треба конкретизувати їх для подібних трик-ків, т.я. саме цю власт-сть дов-ся часто викор-ти при розв’яз-ні задач. При цьому суттєвим є порядок запису вершин подібних трик-ків. Під час вивч. ознак подібності трик-ків варто нагадати відмінність між пон-ми "означення подібних трик-ків" і "ознаки подібних трик-ків". Дов. трьох ознак подібності трик-ків виконуються за однак. схемою, на яку доц. звернути увагу. Т.я при дов. всіх трьох ознак подібності трик-ків викор. ознаки рівності трик-ків, треба до цього повторити ознаки рівності. У систему задач на подібність варто включати задачі практ. змісту на визнач. висоти предметів (телеграф. стовпа, ширини річки...)
19.. Методика проведення перших уроків планіметрії . Осн. мета перших уроків геом. - дати пон. про геометрію, систематизувати наочні уявлення про найпрост. геом. фігури, ввести первісні пон. і поставити учнів перд потребою ввести озн. деяких відомих їм фігур (відрізок, півпряма, півплощина, кут, трик., парал. прямі), розгл-ти первісні та означувані віднош., сформул. осн. власт. найпрост. фігур і власт. вимір-ня відрізків і кутів, які наприкінці теми буде названо аксіомами. Щодо первісних понять планім-ї "точка", "пряма", то уявлення про них учні вже пов. мати з поп-х класів. Варто підкреслити, що точка не має розмірів, пряма не має товщини, кінців і вваж. необмежено продовженою. При форм-ні поняття "належить" для точок і прямих на площині треба зверн. увагу на можл. вжив. різних термінів для познач. цього віднош. (точки належать прямій, точки лежать на прямій, пряма прох. ч-з точки). При форм-ні пон. "лежить між" для трьох точок прямої необх. відмежовувати сформоване в учнів з життєвої практики дане пон. (в геом. воно викор. для познач. власт-ті трьох точок, які належать лише прямій). На поч. курсу геом. з дидакт-х міркувань давати тлумачення терміна "означення" недоцільно. Досить обмежитись роз’ясненням на прикладах пон. "означити що-небудь". Вводити пон. можна як конкретно-індуктивним, так і абстрактно-дедуктивним методом. Учні формулюють означення, вчитель уточнює його. Це стос. означ. понять "розгорнутий кут", "паралельні прямі", "бісектриса кута". Означ. понять "кут", "трикутник", "рівні трикутники", "суміжні кути", "перпендикуляр до прямої"... доцільніше ввести абстр.-дедукт. методом. Вивч. основних власт-тей найпростіших фігур і формулювання кожної власт-ті доцільно починати з розгляду відповідних фігур і практичних дій учнів: вибір точок на прямій і поза нею, проведення прямої через дві дані точки... На цьому етапі навчання вже є можливість пояснити походження і роль первісних понять і аксіом при побудові курсу планіметрії. Пон. про теорему і доведення вчителю дов. ввести перед дов-ням першої т-ми про власт-сть прямої, яка не прох. через жодну вершину рик-ка і перетинає одну зі сторін цього трик-ка. Структуру змісту т-ми (умова і висновок) теж треба пояснити на прикладі формулювання цієї теореми, бо іншого зразка учні не мають. Треба привчати учнів до культури запису на дошці і в зошиті, та показати їм зразок скороченого запису умови і висновку т-ми. Щоб полегшити сприймання учнів першого для них методу доведення від супротивного, треба не лише пояснити його суть, а й дати навчальний алгоритм і орієнтир доцільності використання (неможливість чого-небудь і єдиність в мат-ці завжди дов-ся методом від супрот-го). Система задач на перших уроках спрямована на засвоєння власт-тей найпростіших фігур, на формування вмінь посилатися на аксіому, теореми і означення при дов-ні нових тверджень, розв’язуванні задач на доведення й обчислення, на засвоєння геометричної мови.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.200 (0.013 с.) |

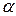 (00 <
(00 < 


