
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна ієрархічна модель та етапи її побудовиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Майже кожну більш-менш складну практичну задачу обґрунтування прийняття рішення доводиться розв’язувати за умов невизначеності, конфлікту й зумовленого ними ризику, з позиції досягнення різних (часто суперечливих) цілей та з використанням при цьому кількох критеріїв оцінювання якості альтернативних рішень (стратегій). Один із підходів до реалізації цієї ідеї — розгляд певної економічної проблеми як ієрархічної структури. Сутність цього підходу полягає в тому, що кожен елемент (інформаційну базу) вищого рівня ієрархії можна розкласти (деталізувати) на кілька часткових елементів нижчого рівня, які, у свою чергу, деталізуються множиною елементів наступного (нижчого) рівня тощо. Цей процес триває доки з’являється можливість побудувати математичні моделі у вигляді цільових функцій (функціоналів оцінювання) для простіших часткових цілей. Слід виокремити такі етапи побудови ієрархічної моделі: 1) формування множини допустимих рішень (стратегій); 2) формування множини цілей та побудова цільових функцій (функціоналів оцінювання); 3) формування набору критеріїв оцінювання якості рішень (стратегій); 4) встановлення шкали їх оцінювання (методу нормалізації); 5) виявлення системи пріоритетів суб’єкта управління; 6) побудова вирішувальних правил. Формування набору критеріїв і розробка шкал їх оцінювання Набір критеріїв вважають повним, якщо використання будь-яких додаткових критеріїв не змінює результатів розв’язання задачі, а відкидання хоча б одного з обраних критеріїв, навпаки, призводить до зміни результатів. Формування набору критеріїв дає змогу виділити ті аспекти наслідків, які повинні братись до уваги при порівнянні різноманітних варіантів рішень. А тому виникає необхідність в розробці шкал для оцінювання критеріїв. Для подальшого переходу до порівняльних шкал щодо елементів функціоналів оцінювання застосовується нормалізація. Деякі методи нормалізації наведено в табл. 6.1. Таблиця 6.1
Виявлення системи пріоритетів прийняття рішення Виявлення системи пріоритетів в межах моделі багатоцільової оптимізації ґрунтується на висловлюванні особи, яка приймає рішення, деяких суджень про вплив певних змін окремих компонент векторних оцінок чи наборів цих компонент на пріоритетність (цінність, корисність) варіантів рішень. Сукупність таких тверджень є інформацією про систему пріоритетів суб’єкта керування. Розглянемо одну з характеристик пріоритету – вектор вагових коефіцієнтів (U). Якщо розглядаються Q об’єктів, то компонента uq вектора вагових коефіцієнтів
Деякі принципи урахування пріоритету наведено в табл. 6.2. Таблиця 6.2
Побудова вирішувальних правил Вирішувальне правило являє собою алгоритм впорядкування векторних оцінок на основі інформації про систему пріоритетів суб’єкта керування. Саме на етапі побудови вирішувального правила проводиться конкретизація поняття „пріоритет” і тим самим визначається впорядкованість рішень.
Згортання інформації Під методом (оператором) згортки інформації, що відповідає певному критерію, розуміють внутрішню частину цього критерію, яка здійснює перетворення початкової інформації (найчастіше заданій у вигляді матриці) до зручного, щодо застосування критеріїв прийняття рішення, вигляду (стовпчика). Отже, етап згортання інформації завжди передує моменту формального вибору рішення серед альтернативних варіантів. Деякі критерії прийняття рішень при наявності зваженої інформації наведено в табл. 6.3.
38. Елементи класифікації задач стохастичного програмування. Приклади задач стохастичного програмування. Типову задачу математичного програмування в детермінованій постановці формулюють так: визначити вектор
Якщо функції в даній задачі крім керованих параметрів Х залежать ще і від деяких випадкових величин
де Ω — простір подій ω. Залежно від можливості отримати та врахувати інформацію стосовно детермінованості (стохастичності) функцій I) стохастичні коефіцієнти цільової функції та детерміновані обмеження; II) детерміновані коефіцієнти цільової функції та стохастичні вільні члени і коефіцієнти системи обмежень; III) стохастичні коефіцієнти цільової функції, вільні члени і коефіцієнти системи обмежень. Конкретні постановки задач СП мають свою специфіку. Передусім необхідно визначити: 1. Детермінованим чи випадковим є вектор Х. Якщо вектор Х є детермінованим, то він не залежить від випадкових параметрів моделі. Якщо ж він випадковий, то тоді Х є функцією від ω — 2. Як розуміти максимізацію (мінімізацію) цільової функції — як абсолютну (для всіх значень 3. Як виконуються обмеження: абсолютно для всіх При постановці задач стохастичного програмування необхідно виходити не лише з математичних міркувань, а й з економічного зміст. Методи розв’язування стохастичних задач поділяють на дві групи — прямі та непрямі. Прямі методи використовують для розв’язування задач стохастичного програмування, коли існують способи побудови функцій
39. Одноетапні статичні задачі управління виробництвом за умов ризику. Під статичними розуміють такі моделями, всі параметри яких протягом всього періоду управління залишаться незмінними або ж їх зміною можна знехтувати. Вивчення статичних моделей є доцільним, якщо необхідно встановити початковий рівень виробництва нових товарів, що є відправним етапом для подальшого розв’язку динамічних задач управління виробництвом. В однокрокових задачах нехтують також динамікою надходження інформації, рішення приймаються на основі інформації, яка існує на момент прийняття рішення на початку інтервалу (періоду) управління (планування). Рішення за цих умов є детермінованим. Розглянемо виробничо-економічну систему з певною потужністю х, попит на які на ринку (у споживача) заздалегідь не відомий і вважається випадковою величиною Cо є О,. Позначимо через q(x) величину загальних витрат при виробництві продукції, а через f(x, Cо) збитки, яких зазнає виробництво від недовипуску продукції, якщо Cо>х, через/^х, Cо) — збитки, що виникають тоді, коли виробництво перевищує величину випадкового попиту, тобто коли х>Cо. Таким чином, задача полягає у знаходженні такої кількості товару х, який мінімізує сумарні сподівані витрати, що складаються із вартості виробництва, тобто F(x) = q(x) + Mf(x,Co) —> min(1) при обмеженнях хє X,(2) де X — деяка множина я-мірного простору, яка може бути утворена обмеженням, пов’язаним з потужністю підприємства, обсягами продукції. У разі якщо максимізується прибуток від реалізації продукції, яка виробляється. F(x) = q(x) - Mf(x, Co) —> max. Типові труднощі, які виникають при розв’язуванні однокро-кової задачі (1), (2), полягають у складності (або неможливості) точного обчислення значень функції сподіваних витрат F(x) та її градієнта, що пов’язано з обчисленням інтегралу виду F(x) = q(x) + f(x, CO)d(p{co) з n де (p(co) — функція розподілу випадкового параметру. 40. Двохетапні задачі управління виробництвом за умов ризику. Розглянемо задачу стохастичного програмування в такій постановці:
Якщо обмеження залежно від значень випадкових параметрів та вектора Х виконуються як
За виконання обмежень залежно від значень випадкових параметрів та вектора Х у вигляді
Допустимо також, що відомі величини
Тоді доцільно розв’язувати задачу (10.10)—(10.12) у такій постановці:
Змінні Отже, розв’язування задачі відбувається в два етапи: спочатку відшукують фіксований план
Важливо спочатку отримати такий план, який би вимагав мінімальних витрат не лише на його реалізацію, але і на його коректування. Коректування планів у процесі їх реалізації є цілком природним при складанні планів для реальних економічних процесів. Необхідність коректування плану зумовлена не недоліками планування, а складністю прийняття рішень за умов невизначеності. Детерміноване моделювання не дає змоги об’єднати два етапи: прийняття плану та його коректування. Перехід від детермінованих моделей до стохастичних, в яких використовуються випадкові величини, що саме і викликають необхідність корекції, уможливлює отримання математичних моделей, що об’єднують вищеназвані два етапи планування. Отже, в результаті розв’язування двохетапних стохастичних задач отримують плани, що є стійкими за умов невизначеності і мінімізують загальні витрати на реалізацію і корекцію плану, тобто забезпечують загальний ефект від попереднього плану та його корекції. У моделях двохетапного стохастичного програмування відображаються найхарактерніші особливості планування за умов невизначеності: 1) ймовірнісний характер початкової інформації, 2) вибір попереднього плану з урахуванням його майбутнього коректування, 3) коректування попередньо вибраного плану по мірі уточнення інформації.
41. Необхідність управління ризиком в спектрі економічних проблем. Досягнення високої ефективності управління економічними ризикамиможливе за умови його відповідного методичного забезпечення, що охоплюєсукупність способів виявлення, методів і методик оцінювання економічних ризиків, а також методів і способів оптимізації їхнього рвня. Вчасне виявлення економічних ризиків допомагає ідентифікувати більшість небезпек, але, зазвичай, через певний час виникають нові. Оперативність реагування на них залежить від якості інформаційного забезпечення, до структури якого потрібно залучати дві підсистеми: - збір загальної поточної інформації про стан об'єкта антиризикового управління; - отримання вихідної інформації про ризикові ситуації, які виникли. Одним із основних завдань управління ризиками є розроблення програми управління ризиками для запобігання настанню небажаної події, мінімізації збитку після виникнення такої небажаної події. У практичній діяльності комплекс заходів щодо управління економічними ризиками знаходить своє втілення в реалізації спрощеного процесу управління ризиками, що охоплює такі етапи: - вибір стратегії управління ризиками, виявлення й оцінювання можливих збитків; - попередній добір ризиків у рамках обраної стратегії; - добір і реалізація превентивних заходів обраними ризиками; - аналіз ризиків після реалізації програми управління ризиками; - оцінка ефективності управління ризиками. Очевидно, що основна мета управління ризиками – стабілізувати отримання підприємством запланованого прибутку, що позитивно впливає його інвестиційну привабливість. Багато в чому успіх управління ризикам залежить від раціональності (своєчасності, доцільності, доречності) використання тих чи інших прийомів. Проте, в разі прийняття підприємством ризиків на себе, повинно виконуватися правило – настання всіх несприятливих подій одночасно має залишати підприємству змогу ефективно функціонувати 42. Запаси, резерви як спосіб зниження ризику. Одним з основних способів мінімізації ризику є створення запасів і резервів. До запасів крім предметів та продуктів праці належать запаси виробничих потужностей, обігових коштів, незавершеного виробництва, кваліфікації кадрів тощо. Матеріальні запаси можна поділити на три види: страховий запас готової продукції на складі; страховий виробничий запас; динамічний страховий запас.
1.загальний резерв грошових коштів покликаний покривати будь-які зміни в кошторисі спричинені впливом факторів ризику; 2.спеціальний резерв, що складається з надбавок не покриття зростання цін і різних затрат за окремими позиціями. Створення запасів і резервів на підприємстві є досить дієвим способом захисту від ризику, але і відносно “дорогим”, оскільки вимагає вилучення грошових коштів з господарського обороту. 43. Структура та види запасів, резервів на непередбачувані витрати. За нестабільного економічного середовища, несвоєчасного виконання прийнятих рішень, помилок в обґрунтуванні оптимального рівня планів тощо виникає істотний (навіть катастрофічний) рівень ризику. У зв’язку з цим менеджерам доцільно вживати відповідних заходів, створюючи резервні фонди (фонди ризику) для страхування несприятливих наслідків, зниження ступеня ризику. Управління запасами пов’язане з проблемою досягнення оптимальної рівноваги між двома конкуруючими чинниками: мінімізацією капіталовкладень у запаси та максимізацією рівня надійності обслуговування споживачів продукцією даного підприємства. До запасів, крім предметів і продуктів праці, належать запаси виробничих потужностей, основних фондів і оборотних коштів, незавершене будівництво, кваліфіковані кадри тощо. Види матеріальних запасів Матеріальні запаси можна умовно розподілити на три види. Перший вид — страховий запас готової продукції на складі, призначений для компенсації коливань попиту на ринку. Враховуючи, що ринок у нашій країні перебуває в стадії формування і характеризується суттєвими і важко передбачуваними коливаннями попиту, підприємства (фірми) змушені формувати страхові запаси готової продукції для компенсації цих коливань, тобто для зниження ступеня ризику. Запаси позитивно впливають на стимулювання попиту, оскільки дилери впевнені, що в будь-який момент вони швидко одержать необхідний обсяг певного товару. Проте необхідно враховувати і негативний вплив запасу на фінансовий стан фірми (підприємства), бо в запасах підприємство фактично «заморожує» частину засобів, вилучаючи їх з обороту. Другий вид — страховий виробничий запас сировини, матеріалів і комплектуючих виробів. Під страховим виробничим запасом розуміють запас, призначений для запобігання ризику раптової зупинки виробництва внаслідок несвоєчасної доставки сировини, матеріалів і комплектуючих виробів. Обсяг цього запасу залежить лише від того, наскільки гарантованим і стабільним є забезпечення підприємства. Третій вид — динамічний виробничий запас, що являє собою запас матеріалів і комплектуючих виробів, який формується з певною періодичністю і в певних обсягах. Головною метою створення динамічно формованих запасів є зниження прямих виробничих затрат (збитків) при стабільному забезпеченні виробництва необхідним обсягом сировини, матеріалів і комплектуючих виробів. На ефективність формування запасів впливають два різноспрямованих випадкових чинники: зростання вартості матеріалів і комплектуючих виробів (інфляція на змінні затрати); зростання вартості капіталу (оборотних засобів). Якщо придбати матеріали і комплектуючі в запас на всю виробничу програму, скажімо на початок року, і використовувати їх у виробництві продукції за «старими» цінами, то в запасах будуть «заморожені» великі кошти, попит на які вимагатиме одержання кредиту в банку під значний відсоток. Необхідність обслуговувати цей борг значно збільшить загальні (постійні) витрати, котрі можуть бути обтяжені значним ризиком. Отже, важливо об’єктивно оцінити стратегію формування запасів, використовуючи їх обсяги і періодичність поповнення як змінні параметри. Обсяг резерву сировини Визначення, наприклад, обсягів резерву сировини (комплектуючих) може спиратися на дані відхилень, що мали місце в минулому (задокументовані) від встановлених (обумовлених) термінів постачання. Величина цього резерву, який служить для зменшення ступеня ризику, встановлюється шляхом перемноження величини, наприклад, добового споживання даної сировини на кількість діб, визначених як середньоквадратичне відхилення фактичного періоду постачання від обумовленого (середньої величини) за контрактом 44. Резервування грошових засобів на покриття випадкових затрат. Створення резерву грошових засобів на покриття випадкових затрат — це один із способів зниження ризику, який передбачає встановлення співвідношення між потенційним ризиком і величиною затрат, необхідних для подолання збоїв у виконанні зобов’язань (проекту). Для визначення обсягів грошей на покриття випадкових затрат (збитків), переоцінки їх в процесі роботи над проектом і уточненням суми резерву на основі фактичних даних можуть бути використані всі викладені у попередньому матеріалі методи якісного і кількісного аналізу ризику. Визначення структури резерву на покриття імовірних непередбачуваних затрат проводиться за допомогою одного з двох можливих способів. Згідно з першим способом (рис. 2.1.13) резерв ділять на дві частини: на загальний і спеціальний. Загальний резерв повинен покривати зміни в кошторисі, добавки до загального обсягу грошей по контракту та інші елементи.
Рис. 2.1.13. Резерви, узгоджені в контракті на покриття ймовірних затрат (збитків) Спеціальний резерв складається з надбавки на покриття зростання цін, зростання затрат по окремих позиціях, а також на сплату позовів по контрактах. Згідно з другим способом (рис. 2.1.14) структура резервів передбачає визначення імовірних затрат (збитків) по видах затрат, наприклад на заробітну плату, матеріали, субконтракти.
Рис. 2.1.14. Визначення структури резервів на покриття ймовірних збитків (затрат) Моделі оптимізації ступеня ризику та деякі стратегії формування запасів Різновиди задач управління запасами та їх складність зумовили створення великої кількості математичних моделей, ефективне використання яких неможливе без застосування економіко-математичних методів та ЕОМ. Найістотнішим чинником, який необхідно враховувати при розробці моделей управління запасами, є час. Статичні моделі управління запасами лише наближено відповідають реальним умовам. Більш точний розв’язок може бути одержаний на базі використання динамічних моделей. Окрім того, в переважній більшості реальних задач попит є випадковою величиною, розподіл імовірності якої може бути як відомим, так і невідомим. Внаслідок цього виникає економічний ризик, зумовлений невизначеністю, стохастичністю щодо величини попиту. Величина ризику може бути визначена як відхилення потреб у запасах від середньої (сподіваної) величини. 45. Задачі управління запасами з урахуванням ризику. Різноманітність задач управління запасами та їх складність привели до створення великої кількості математичних моделей, ефективне використання яких неможливе без застосування економіко-математичних методів та ЕОМ. Моделі управління запасами відрізняються багатьма компонентами, залежно від характеру зміни величин, які до них входять. Найбільш суттєвим чинником, який слід враховувати при розробці моделей управління запасами, є час. Статичні моделі управління запасами лише наближено від-повідають реальним умовам. Більш точний розв’язок можна одер-жати на базі використання динамічних моделей, які враховують час та відповідні залежності. Слід відзначити, що в багатьох моделях управління запасами одним із головних припущень є те, що, наприклад, попит є зазда-легідь відомою детермінованою величиною. Однак у переважній більшості реальних задач він є випадковою величиною, розподіл імовірності якої може бути як відомим, так і невідомим. Аналіз, моделювання та управління економічними ризиками з цим виникає економічний ризик, зумовлений невизначеністю, стохастичністю щодо величини попиту. Величина ризику може бути визначена як відхилення споді-ваних результатів щодо потреб у запасах від середньої або споді-ваної величини. Управління запасами за умов невизначеності [9] Стратегія управління запасами при невизначеному (стохас-тичному) попиті вимагає створення певного резерву заздалегідь визначеного обсягу К, а потім здійснюються чергові поставки за-пасів. Якщо в певний момент часу загальний запас знижується до обсягів резерву, терміново оформляють заявку на постачання нової партії. Якщо ж її виконання потребує певного часу, то вона подається тоді, коли запас знизиться до рівня K+L. Одним із найпростіших способів, який дозволяє вирішити про-блему резерву, є застосування принципу гарантованого результату, тобто обрання досить великого резерву, який гарантує мінімаль-ний ризик, — компенсацію будь-яких випадкових відхилень, що вимагає значних витрат на їх зберігання тощо. Це також призво-дить до так званого ризику невикористаних можливостей, тому що великі резерви пов’язані з відволіканням значних коштів. У та-кому випадку вводяться додаткові гіпотези, в основу розрахунку необхідного резерву закладається поняття допустимого ризику — ймовірності того, що потреба в запасах не перевищить наявного резерву. Вводиться поняття коефіцієнта ризику, який виражає імовірність того, що потреби у запасах виявляться незадовільни-ми через недостатність резерву і перевищать його обсяг. Значення коефіцієнта ризику може дорівнювати 5 чи 1%. Позначимо через Гпотребу в продукції між двома поставками і сформулюємо задачу. Необхідно визначити такий обсяг резерву К, щоб коефіцієнт ризикур, тобто імовірність того, що резерв виявиться недо-статнім, був би не більшим (рівним) від заданої величини, тобто P(V > q + К) < р чи P((V -q) > К) < р, Останкова Л. А., Шевченко Н. Ю. де q — обсяг постачання (розмір партії), який можна розгля-дати як детерміновану величину. Для визначення К необхідно знати закон розподілу випадкової величини V. Тут можливим є декілька варіантів та гіпотез. Припустимо, що потреба в запасах, тобто величина V, розподі-лена за нормальним законом з параметрами q та а2, де a — серед-ньоквадратичне відхилення. Позначимо и = (V -q)/(J. Тепер можна записати вираз для щільності імовірностей: -и2 p(u) 2ГпЄ Задача полягає у знаходженні величини и = (V-q)/(7, що залежить від коефіцієнта ризику (імовірності)р, для якого спра-ведливе рівняння CO -U2 1 Г -2, \е аи = pz. лІ2ж J За змістом прийнятих допущень резерв К має бути таким, щоб імовірність появи дефіциту дорівнювала». Тоді із и = (V-q)/а виходить, що резерв, який відповідає коефіцієнту ризику р, повинен дорівнювати щонайменше K>(V-q) = u a. (200) Тому якщо, наприклад, р = 0,05, тоК = 1,64а. Можна зробити висновок, що розміри резерву К визначаються прийнятим коефіцієнтом ризику (р) та коливанням (розкидом) потреб у запасах, що характеризуються середньоквадратичним від- 146 Аналіз, моделювання та управління економічними ризиками хиленням а, величина якого наближено визначається на базі ста-тистичної обробки значень попиту за попередні періоди. Якщо позначити через Ь сподівану інтенсивність попиту, то за-гальні витрати на управління запасами складуть: B(q) = c 1 b/q + c 2 (q/2 + u (7), (201) де Cj — витрати на оформлення партії, які не залежать від роз-міру (обсягу) партії і виникають кожного разу під час її розміщення; с2 — витрати на зберігання одиниці запасу за одиницю часу; B(q) — сумарні витрати на утримання запасу за одиницю часу. Ці витрати будуть мінімальними, якщо dB(q)/dq — —cfi/q2 + с2 /2 — 0 Звідси можна визначити величину оптимального розміру пар-тії: 2 1 (202) V С2 Отже, на розмір партії резерв не впливає. Оптимальний запас разом із резервом дорівнює: W = 1 +и О, (203) V С2 де W — необхідний запас разом з резервом.
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 589; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.016 с.) |

 ;
; 
 ;
; 
 ;
; 


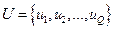 є величиною, що визначає відносну перевагу q–го об’єкта над рештою. Компоненти вагового вектора U зв’язані між собою співвідношеннями:
є величиною, що визначає відносну перевагу q–го об’єкта над рештою. Компоненти вагового вектора U зв’язані між собою співвідношеннями:




 і хоча б для одного значення
і хоча б для одного значення 
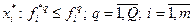 і хоча б для одного значення
і хоча б для одного значення











 , для компонент якого:
, для компонент якого: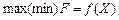 ,
, ,
, .
. , то маємо задачу стохастичного програмування:
, то маємо задачу стохастичного програмування: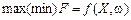 ,
, ,
, ,
, ,
,  постановки задач СП можуть містити:
постановки задач СП можуть містити: , тобто залежить від випадкових змінних.
, тобто залежить від випадкових змінних. ) чи як максимізацію її математичного сподівання або деякої іншої ймовірнісної характеристики цієї функції (моди, медіани), або як мінімізацію середнього квадратичного відхилення?
) чи як максимізацію її математичного сподівання або деякої іншої ймовірнісної характеристики цієї функції (моди, медіани), або як мінімізацію середнього квадратичного відхилення? на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до ЗЛП чи ЗНП, тобто перехід до детермінованого аналога задачі стохастичного програмування.
на базі інформації щодо параметра ω. Непрямими є методи зведення стохастичної задачі до ЗЛП чи ЗНП, тобто перехід до детермінованого аналога задачі стохастичного програмування. , (10.10)
, (10.10) ; (10.11)
; (10.11)
 . (10.12)
. (10.12) , то можливе існування надлишку (ресурсів, продукції тощо). Позначимо його через
, то можливе існування надлишку (ресурсів, продукції тощо). Позначимо його через  :
: .
. виникає дефіцит. Позначимо його через
виникає дефіцит. Позначимо його через  :
: .
. — питомі витрати на збереження надлишків
— питомі витрати на збереження надлишків  та
та  — питомі витрати, що пов’язані з дефіцитом
— питомі витрати, що пов’язані з дефіцитом 
 . Отже, можна визначити штрафну функцію для і -го обмеження за результатом його виконання. Позначимо її через S, тоді:
. Отже, можна визначити штрафну функцію для і -го обмеження за результатом його виконання. Позначимо її через S, тоді:


 , (10.13)
, (10.13) згідно з апріорною інформацією про стан зовнішнього середовища, який і визначає реалізацію випадкових параметрів. Значення вектора Х не задовольняє обмеження задачі для кожного
згідно з апріорною інформацією про стан зовнішнього середовища, який і визначає реалізацію випадкових параметрів. Значення вектора Х не задовольняє обмеження задачі для кожного  . На другому етапі після спостереження за зовнішнім середовищем і отримання точного значення випадкових параметрів ω знаходять значення змінних
. На другому етапі після спостереження за зовнішнім середовищем і отримання точного значення випадкових параметрів ω знаходять значення змінних  .
.




