
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні засади класифікації ризикуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тенденція до ускладнення соціально-економічних процесів породжує появу все нових видів і типів ризику. Ризик, як правило, поділяють на два типи — динамічний і статичний. Динамічний ризик — це ризик, пов’язаний з непередбачуваними (недетермінованими) змінами вартості основного капіталу внаслідок прийняття управлінських рішень або непередбачуваними зсувами у ринкових чи політичних реаліях. Такі зміни можуть призвести як до збитків, так і до додаткових прибутків. Статичний ризик — це ризик, пов’язаний зі скороченням реальних активів внаслідок втрати частки власності, а також із скороченням доходу через недієздатність організації. Цей ризик може призвести лише до збитків. Видове різноманіття ризиків дуже велике — від пожеж і стихійних лих до міжнаціональних конфліктів, змін у законодавстві, що регулює економічну та підприємницьку діяльність, інфляційних коливань тощо. В економічній літературі, присвяченій проблемам класифікації ризику, на наш погляд, ще немає чіткої системи класифікації ризиків. Існує низка підходів до цього. Очевидно чинником ризику є все оточуюче нас довкілля, а також усі елементи об’єкта дослідження як складної економіко-кібернетичної системи (джерелами ризику є всі елементи системи, її прямі та зворотні зв’язки). Певний інтерес становить класифікація ризику, здійснена відомим економістом Й. Шумпетером, який виокремлює два види ризику: · ризик, пов’язаний з можливим технічним провалом виробництва. Сюди він відносить також загрозу втрати благ, пожежі, пошкодження, зумовлені стихійними лихами; · ризик, пов’язаний з відсутністю комерційного успіху. Класифікують ризики і за такими ознаками: · ризик, пов’язаний з господарською діяльністю; · ризик, пов’язаний з особистістю підприємця; · ризик, пов’язаний з неповною інформацією щодо стану довкілля. У праці [8] наводиться глосарій ризиків, які, в свою чергу, поділяються на види. Зокрема, серед груп ризиків наведено такі: · країнні ризики (політичні та макроекономічні); · маркетингові ризики; · транспортні ризики; · ризики визначення предмета угоди; · ризики умови кількості; · ризики умови якості; · ризики умови упаковки та маркування; · ризики умови ціни; · ризики умови постачання;
· ризики валютно-фінансових умов контракту; · ризики умов форс-мажорних обставин; · ризики визначення умов розгляду арбітражу; · комерційні ризики; · ризики, пов’язані з процесом митного оформлення тощо. У низці наукових праць запропоновано таку класифікацію ризику [1]: · за масштабами та обсягами (глобальний, локальний); · за аспектами (психологічний, соціальний, економічний, екологічний, юридичний, політичний, медико-біологічний); · за мірою об’єктивності та суб’єктивності (з об’єктивною ймовірністю, з суб’єктивною ймовірністю, з об’єктивно-суб’єктивною ймовірністю); · за ступенем (мірою) ризиконасиченості рішень (мінімальний, середній, оптимальний або ж допустимий, критичний, катастрофічний); · за мірою обґрунтованості ризику (раціональний, нераціональний, авантюрний); · за терміном оцінки та урахування ризику (випереджаючий, своєчасний, запізнілий); · за чисельністю осіб, які беруть участь у прийнятті рішень (індивідуальний, груповий, колективний); · за ситуаційним класом джерел (в умовах невизначеності, в умовах конфлікту (конкуренції), в умовах розпливчастості (нечіткості)). Кожний вид ризику, в свою чергу, доцільно детально розкласти на елементи, проаналізувати, змоделювати, урахувати, що дасть змогу певною мірою зменшити ступінь невизначеності та її руйнівні дії. 9. Оцінка ступеня ризику в абсолютному виразі. Серед кількісних методів виділяють оцінку ризику в абсолютному і відносному вираженні. В абсолютному вираженні ризик вимірюється іменованими величинами, наприклад, частотою чи розмірами можливих збитків у грошовому еквіваленті. Розглянемо основні способи кількісної оцінки ризику, при цьому кількісну оцінку ризику будемо позначати R. Оцінюючи ризик, на практиці нерідко обмежуються спрощеними підходами, спираються на один або кілька основних показників та критеріїв, які являють собою найважливіші узагальнені характеристики у даній конкретній ситуації. У короткотерміновому прогнозуванні існує досить проста методика визначення коефіцієнта ризику. Якщо ймовірність достовірності прогнозу рівна p, то ймовірність того, що прогноз не справдиться дорівнює 1-p. Відповідно коефіцієнт ризику складає величину 1-p.
R=1-p. У ряді випадків, зокрема у страхуванні, величину (ступінь) ризику визначають як ймовірність настання небажаних наслідків рн: R=pн. В абсолютному вираженні ступінь ризику невдачі визначається якк дбуток ймовірності невдачі на величину небажаних наслідків (збитків, платежів), які мають місце в цьому випадку, тобто: R=pн Більщ точною оцінкою ризику є така, яка ґрунтується на всьому спектрі можливих результатів. Якщо є відомими всі можливі наслідки певної події та ймовірності їх настання, то для оцінки ризику використовують величину сподіваного значення (математичне сподівання) Також при абсолютному вираженні міри ризику під час прийняття економічних рішень широко використовується дисперсійний підхід. D(x) = M(x-M(x))2.
10. Оцінка ступеня ризику у відносному виразі. Серед кількісних методів виділяють оцінку ризику в абсолютному і відносному вираженні. У відносному вираженні ризик вимірюється різними безрозмірними показниками, що є відношеннями двох чи кількох іменованих величин. У відносному вираженні ризик визначається як величина можливих збитків, віднесена до деякої бази. За базу зручно приймати або майно підприємця, або загальні витрати ресурсів на даний вид підприємницької діяльності, або очікуваний прибуток від даного підприємства. Для підприємства за базу визначення відносної величини ризику беруть вартість основних виробничих фондів та оборотних засобів або планові сумарні затрати на даний вид діяльності. Співвідношення максимального можливого обсягу збитків до обсягу власних ресурсів інвестора є мірою ризику, тобто: У відносному вираженні ризик також вимірюють за допомогою коефіцієнта варіації, тобто відношення середньоквадратичного відхилення економічного показника х до сподіваного значення цього показника: Коефіцієнт варіації як безробітна величина дає можливість порівнювати результати двох проектів, які неможливо порівняти в абсолютному вираженні, тобто таких, які оцінюються різними найменуваннями, причому чим більше значення CV(x), тим більша величина ризику.
11. Ризик та нерівність Чебишева. Правило „трьох сігм”. Дисперсія, як міра ризику, дозволяє виявити граничні шанси особи, яка приймає рішення. Теоретична база цієї властивості дисперсії закладена в нерівності Чебешева: ймовірність того що випадкова величинаа х відхиляється за модулем від свого математичного сподівання більша, ніж наперед заданий допуск Математично нерівність Чебешева записується так: Слід зауважити, що оскільки Р ≤ 1, то і Розглянмо ситуацію, коли інвестиції здійснюються за рахунок кредиту, взятого під rs(%) під заставу нерухомості. Постає питання, що випадкова величина х приймає значення, яке відповідає умові Звідси слідує правило «трьох сігм» 12. Поняття допустимого, критичного та катастрофічного ризику.
Аналіз ризику можна здійснювати також з точки зору можливих (ймовірних) збитків, що є характерними для будь-якого об’єкта (проекту). Для здійснення цього аналізу вводиться поняття областей (зон) ризику. Виділяють такі зони ризику:
1. Безризикова зона — це область, у якій випадкові збитки не очікуються. Їй відповідають нульові збитки чи перевищення прибутку над сподіваним значенням. Ця область — область виграшу підприємця. 2. Зона допустимого ризику — це область, у межах якої зберігається економічна доцільність підприємницької діяльності, тобто випадкові збитки можуть мати місце, але вони менші сподіваного прибутку від підприємницької діяльності. 3. Зона критичного ризику — це область, де є наявною можливість збитків, які перевищують величину (обсяг) очікуваних прибутків аж до величини повної обчисленої (розрахункової) виручки від підприємницької діяльності. Величина можливих (ймовірних) збитків у цій зоні перевищує сподіваний прибуток і може призвести до втрати всіх коштів, вкладених підприємцем у справу. 4. Зона катастрофічного ризику — це область можливих збитків, які за своєю величиною (обсягом) перевершують критичний рівень і можуть досягати величини (обсягу) майнового стану підприємця. Катастрофічний ризик може призвести до краху, банкрутства компанії (фірми), її закриття і розпродажу її майна. До категорії катастрофічного ризику слід віднести також ризик, пов’язаний з безпосередньою загрозою для життя чи екологічною катастрофою. 13. Оцінка ризику ліквідності. Потреба в оцінці ризику ліквідності виникає під час змін стратегії й тактики інвестиційної діяльності, і оскільки на підприємстві такі зміни відбуваються постійно відповідно і контроль за зміною цього ризику повинен здійснюватись постійно. Ризик ліквідності – це специфічна форма ризику, яка визначається, як ймовірність того, що підприємство не здатне буде виконувати свої фінансові зобов’язання. Він може бути викликаний як низькою віддачею об’єктів інвестування підприємства так і великим періодом інвестиційного процесу. Для оцінки ризику ліквідності використовують два критерії: - час трансформації інвестицій у грошові кошти; - обсяг фінансових втрат інвестора, що пов’язаний з такою трансформацією. За часом трансформації інвестицій у грошові засоби всі об’єкти інвестування можна поділити на: - терміноволіквідні з незначним ризиком (час трансформації до 7 днів); - високоліквідні інвестиції з низьким ризиком (час трансформації від 7 до 30 днів);
- середньоліквідні із середнім ризиком (час трансформації від 1 до 3 місяців); - малоліквідні об’єкти з високим ризиком (час трансформації більше 3 місяців). Виходячи з цього для оцінки ризику ліквідності інвестиційного портфелю підприємства за критерієм часу розраховують такі показники: 1). Частка терміноволіквідних інвестицій в їх реальному обсязі
2). Показник ризику ліквідності
Вс – вартість середньоліквідних активів; Вн – вартість низьколіквідних активів. Чим більшим є показник ризику ліквідності. Тим меншим є ризик ліквідності. Оцінка ліквідності інвестицій за рівнем фінансових втрат здійснюється на основі розрахунку процентного співвідношення величини можливих втрат до обсягів інвестицій, які прагнуть реалізувати. За цим критерієм всі об’єкти інвестування оцінюють як: - з дуже високим ризиком (втрати перевищують 20%); - з високим ризиком (11-20%); - із середнім ризиком (6-10%); - з низьким ризиком (до 5%). Показники ризику ліквідності за критерієм часу й рівнем фінансових втрат знаходяться між собою в оберненій залежності: інвестор згоден на більший рівень фінансових втрат під час реалізації проекту, якщо при цьому він швидше його реалізує, і навпаки. 14. Коефіцієнт чутливості Одним з основних показників, які застосовують при аналізі фінансових ризиків є: показник систематичного ризику або коефіцієнт чутливості β. Систематичний ризик – це ризик, що характеризує цінні папери і пов’язаний із ймовірністю подій, які впливають на весь фондовий ринок вцілому. Тобто не залежить від виду цінних паперів, а тому не усувається шляхом диверсифікації. Показник β кількісно характеризує змінюваність доходів певної акції (цінного паперу) відносно доходів по середньому портфелю, яким в найширшому випадку є весь ринок цінних паперів. Показник β для середньоринкової акції дорівнює 1. Крім того, показник β певного активу характеризує щільність або тісноту зв’язку між біржовим курсом цього активу та загальним станом ринку. Показник β розраховується за залежністю: β = R· де σі, σр – середньоквадратичні відхилення норм доходності відповідно і-того активу та ринкового індексу, R – коефіцієнт кореляції, тобто тісноти зв’язку між нормою доходності і-того активу і зміною ринкового індексу. Якщо β певного активу менший 1. То він має менший систематичний ризик ніж середньоринковий (середній по портфелю). Відповідно, якщо β=1, то має такий самий систематичний ризик, а якщо β>1, то більший за середньоринковий або середній по портфелю, що досліджується. 15. Сутність концепції теорії корисності. Для задач прийняття рішень за умов невизначеності та ризику принцип оптималь-ності нерідко будується у вигляді функції корисності. Оскільки при наявності ризику результати рішень залежать від випадкових величин, то для порівняння їх ефектив-ності необхідно вміти порівнювати функції розподілу ефективності. У цьому випадку важливе значення для прийняття рішень мають результати про властивості функцій корисності.
Корисність визначає ступінь задоволення, яке одержує суб’єкт від споживання то-вару чи виконання будь – якої дії. Найбільш загальний підхід щодо оцінки ступеня (міри) ризику полягає у введенні функції корисності. Концепція функції корисності є одним з важливих елементів будь – якої сучасної економічної теорії. Вона дозволяє здійснити співвимірність споживчих елементів різних товарів. Корисність включає важливу психологічну компоненту, тому що люди досягають корисності, отримуючи речі, що приносять їм задоволення. В економічному аналізі корисність часто використовується для того, щоб описати пріоритети при ранжуванні наборів споживчих товарів та послуг. Застосовуючи різні функції корисності, можна описати будь – які варіанти оцінки випадкової економічної ситуації у вигляді сподіваного значення такої функції. Введемо таке поняття як пріоритет, яке досить часто використовується суб’єктами прийняття рішень. Позначимо поняття “пріоритетніше ніж”, ”байдуже”, “не гірше ніж” відповідними символами >, ~, >~. Нестроге співвідношення пріоритетності “ не гірше ніж” є одним із основних найпростіших понять; його записують так: x >~ y, (4.1) де x та y є набором товарів чи послуг (точками простору Х). Цей запис означає, що певний суб’єкт (споживач) вважає для себе набір х або пріоритетнішим ніж набір у, або не робить між ними різниці, тобто х не гірший ніж у. Можна визначити поняття байдужості та строгої пріоритетності у термінах нестрого-го співвідношення пріоритетності: набори товарів х та у байдужі (еквівалентні) для споживача (х ~ у) тоді і лише тоді, коли x >~ y та y >~ х. (4.2) А коли споживач бажає обрати х, а не у, тобто х пріоритетніше, ніж у (записують х > у), тоді і лише тоді, якщо х не гірше ніж у, а у не гірше ніж х. Значить х > у тоді і лише тоді, коли x >~ y, а x >~ y – несправедливе. (4.3) Надалі будемо вважати, що нестроге співвідношення пріоритетності задовольняє дві основні аксіоми. Перша аксіома стверджує, що це співвідношення є досконалою напівупорядкованістю у просторі товарів Х. Співвідношення називається досконалим, якщо для двох заданих наборів товарів х та у з Х справедливе одне з двох співвідношень: x >~ y, або y >~ х, або одночасно. (4.4) Це означає, що у просторі товарів немає таких “білих плям”, де пріоритет не існує. Співвідношення називають частковою впорядкованістю, якщо воно транзитивне, тоб-то для трьох заданих наборів х, у та z із Х виконується умова: якщо x >~ y та y >z, то x >z, (4.5) що виражає сумісність пріоритетів. І, якщо співвідношення рефлексивне, тобто для будь – якого х є Х: x >~ x. (4.6) Цей факт випливає з досконалості співвідношення. Нестроге співвідношення пріоритетності є досконалою частковою впорядко-ваністю простору товарів і означає, що співвідношення байдужості є співвідношенням еквівалентності, яке транзитивне, оскільки при заданих х, у та z є Х, якщо x ~ y та y ~ z, тоді x ~z - рефлексивне, (4.7) оскільки при заданому х є Х: x ~ x, (4.8) та симетричне, оскільки при заданих х та у є Х: x ~ y означає y ~ x. (4.9) Для доведення, наприклад, транзитивності зазначимо, що x ~ y та y ~ x означає з визначення байдужості, що x >~ у та у >~ z і що z >~ у та у >~ х. Тоді з транзитивності нестрогого співвідношення пріоритетності x >~z та z >~ х випливає, що х ~ z. Співвідношення байдужості, як співвідношення еквівалентності, ділить простір то-варів Х на класи еквівалентності – підмножини, що попарно не перетинаються, нази-ваються множинами байдужості, кожна з яких складається з усіх наборів, байдужих заданому наборові Іх = { у є Х| у ~ х} (4.10) Друга основна аксіома стверджує, що нестроге співвідношення пріоритетності не-перервне, тобто пріоритетні множини, кожна з яких складається з усіх наборів, що є пріоритетніші чи байдужі заданому набору Х: Рх = {у єХ| у >~ х}, (4.11) і непріоритетні множини, кожна з яких складається з усіх таких наборів, для яких заданий набір Х пріоритетніший чи байдужий NPx = {y є X|x >~y}, (4.12) є замкнутою множиною простору товарів для будь – якого х є Х. За цією аксіомою обидві множини містять усі граничні точки, причому для обох множин ці точки утворюють множину байдужості Іх, рівну перетинові РхINPx. З цих основних аксіом досконалої нестрогої впорядкованості та неперервності ви-пливає, що існує неперервна дійсна функція, визначена на елементах множини Х є U(o), котру називають функцією корисності і для якої U(x) >~U(y), якщо х >~ у. (4.13) Функція корисності зіставляє кожному наборові споживчих товарів певне число в такий спосіб, що, якщо набір А пріоритетніший, ніж набір В (А > В), то число, яке відповідає набору А, буде більшим, ніж те, що відповідає набору В. Гранична корисність вимірює додаткове задоволення, яке отримує особа від спо-живання додаткової кількості товару. Наприклад, гранична корисність, що пов’язана із зростанням споживання від 1 до 5 одиниць шоколаду, може дорівнювати 10, від 6 до 10 одиниць – 5, а від 11 до 15 оди-ниць – 3. Ці цифри узгоджуються з принципом зниження граничної корисності. У міру зростання споживання товару процес додаткового споживання дає усе менший приріст корисності. 16. Корисність за Нейманом-Моргенштерном. Теорія сподіваної корисності. Поняття лотереї Для визначення корисності розглядається вибір особи в умовах ризику, який формалізується за допомогою поняття лотереї. Для цього необхідно з множини Х пред’явлених експертам значень певного економічного показника (об’єкта) виділити два значення х* та х* таких, що х 1) значення показника х; 2) лотерею: одержати х *з імовірністю 1 – р чи х* з імовірністю р. Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L (х*, p, x *) не стануть еквівалентними, тобто x ~ L (х *, p, х*). Максимальному й мінімальному значенням х* та х* приписують довільні числові значення U*= U (х *) та U * = U (x*), але так, щоб U* > U*. Під лотереєю L (x*, p (x), x *)розуміють ситуацію, у якій особа може отримати х *з імовірністю р (х) або х *з імовірністю За Нейманом корисність варіанта х визначається ймовірністю U (х) = р (х),при якій особі байдуже, що обирати: х — гарантовано, чи лотерею L (х*, р (х), х*), де х *, х *— вектори, більш та менш пріоритетні порівняно з х. Наприклад, у якості функції корисності можна брати функцію бо для всіх x Î [ x*, x *] значення q (х) Î [0; 1]. Оскільки при зростанні х від х *до х *значення q(х) будуть збільшуватися, то вибрана таким чином функція корисності буде зростаючою. Якщо покласти то в цьому випадку ми отримаємо спадаючу функцію корисності (p (x) = 1 – q (x); p (x) Î [0, 1] для x Î [ x *, х *]). У якості функції корисності (згідно з Нейманом) можна використати функції розподілу ймовірностей: U (x) = F (x) = P (X < x). Hаприклад: Сподівана корисність Нехай L — лотерея, що приводить до виграшів (подій) x 1, х 2,...., хn з відповідними ймовірностями p 1, p 2,..., pn. Позначимо сподіваний виграш (математичне сподівання виграшу) через Справедлива основна формула теорії сподіваної корисності: тобто корисність ансамблю результатів збігається з математичним сподіванням корисності результатів. 17. Поняття лотереї, сподіваного виграшу, детермінованого еквіваленту лотереї, премії за ризик. Лотерея – це ситуація, в якій особа може одержати виграш Лотерею позначають: Такий вид лотереї називають простою лотереєю (коли є 2 виграші). Складена лотерея – це та, в якій можливі n-виграшів Складена лотерея позначається: Для аналізу лотереї використовують ряд показників: 1) сподіваний виграш лотереї, який обчислюється за формулою:
Для простої лотереї: 2) сподівана корисність:
Для простої лотереї:
3) детермінований еквівалент – це гарантована сума Детермінований еквівалент визначається з рівняння:
Якщо можливі виграші описуються щільністю розподілу f(x) то:
А детермінований еквівалент можна знайти зі співвідношення:
4) премія за ризик (П(х)) – це та сума, якою ОПР готова знехтувати(відмовитись) із свого середнього виграшу, щоб уникнути ризику, пов’язаного з лотереєю. П(х)= 18. Різне ставлення суб’єктів до ризику та функція корисності.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.253.240 (0.011 с.) |

 . де pн – ймовірність небажаних наслідків;
. де pн – ймовірність небажаних наслідків;  – величина(розмір) небажаних наслідків.
– величина(розмір) небажаних наслідків. .
.
 , де х- максимально можливий обсяг збитків; к- обсяг фінансових ресурсів.
, де х- максимально можливий обсяг збитків; к- обсяг фінансових ресурсів. . Величину CV(x) можна трактувати як кількість одиниць
. Величину CV(x) можна трактувати як кількість одиниць  , що припадає на одиницю М(х) або величину ризику, що припадає на одиницю доходу.
, що припадає на одиницю М(х) або величину ризику, що припадає на одиницю доходу.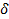 , не перевищує її дисперсії, поділеної на квадрат цього допуску.
, не перевищує її дисперсії, поділеної на квадрат цього допуску. .
. ≤ 1, а отже квадрат заданого допуску, тобто
≤ 1, а отже квадрат заданого допуску, тобто  .
. . Звідси слідує, що шанс збанкрутувати не перевищує величини
. Звідси слідує, що шанс збанкрутувати не перевищує величини  . Ця оцінка має сенс лише тоді, коли виконується умова
. Ця оцінка має сенс лише тоді, коли виконується умова 
 .
.
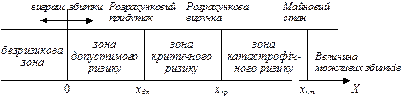
 (2.22),
(2.22),  (2.23),
(2.23), (бета).
(бета). (2.24),
(2.24), х *та х
х *та х  х *для всіх х Î Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне, в певному сенсі, значення показника (разом з «нулем» вони визначають масштаб даної шкали). Власне, так побудована функція корисності Дж. ф. Неймана і О.Моргенштерна. Експерту пропонують порівняти між собою дві альтернативи:
х *для всіх х Î Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне, в певному сенсі, значення показника (разом з «нулем» вони визначають масштаб даної шкали). Власне, так побудована функція корисності Дж. ф. Неймана і О.Моргенштерна. Експерту пропонують порівняти між собою дві альтернативи:


 :
:  ;
; 

 з ймовірністю р, або
з ймовірністю р, або  з ймовірністю 1-р.
з ймовірністю 1-р. або
або 
 з ймовірностями
з ймовірностями 





 , одержання якої еквівалентним участі у лотереї.
, одержання якої еквівалентним участі у лотереї.


 -
-  .
.


