
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несхильність та схильність до ризикуСодержание книги
Поиск на нашем сайте
Вигляд функції корисності може дати інформацію про ставлення до ризику особи, яка приймає рішення. Особу, яка приймає рішення, називають несхильною до ризику, якщо для неї більш пріоритетною є можливість одержати гарантовано сподіваний виграш у лотереї, аніж брати в ній участь. З попереднього відомо, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Отже, умова несхильності до ризику записується як U (M (X)) > M (U (X)). · Твердження 1. Особа, яка приймає рішення, не схильна до ризику тоді і тільки тоді, коли її функція корисності опукла вгору. Особу, яка приймає рішення, називають схильною до ризику, якщо для неї більш пріоритетною є участь у лотереї, ніж можливість одержати гарантовано сподіваний виграш. Отже, умова схильності до ризику записується як U (M (X)) < M (U (X)). · Твердження 2. Особа, яка приймає ріщення, схильна до ризику в тому i тільки в тому випадку, коли її функція корисності опукла вниз.
Рис. 4.2. Функція корисності особи, несхильної до ризику Графічне доведення справедливості тверджень 1 та 2 для лотереї L(x1, p; x2,q), p +q=1, наведене відповідно на рис.4.2 та рис.4.3 (там`
Рис. 4.3. Функція корисності особи, схильної до ризику Функція схильності-несхильності до ризику При різних рівнях доходу (багатства) ставлення людини до ризику може змінюватись. Досить реалістичною гіпотезою для широкого кола суб’єктів є схильність до ризику при невеликих сумах (відносно загального достатку) та несхильність при значних сумах. Графічно ця гіпотеза зображена на рис. 4.4.
Що стосується функцій, які описують висунуту гіпотезу, то їх будемо називати функціями схильності-несхильності до ризику (С-НСР). Можна зробити висновок, що ставлення до ризику — це локальна характеристика особи. Якщо людина більш заможна, то вона може дозволити собі ризикнути більшою сумою. Чим заможніша людина, тим більш праворуч на графіку її функції С-НСР розташована зона несхильності до ризику (точка а). Аналітично функції корисності такого типу можна задати за допомогою зрізаних функцій розподілу ймовірностей, а саме:
Наприклад, виходячи з нормального закону розподілу, що має параметри m та s, отримуємо:
Несхильність (або нейтральність) до ризику використовується страховими компаніями, які скуповують ризик. На схильності до ризику функціонує гральний бізнес. Нейтральність до ризику Проміжне значення між схильністю та несхильністю до ризику відіграє нейтральність (байдужість) до ризику. Вона визначається байдужістю особи у виборі між отриманням гарантованої суми, яка збігається з середньоочікуваним виграшем, та участю у лотереї. Очевидно, що а) функція корисності для особи, нейтральної до ризику, є лінійною, тобто U (x) = ax + b; б) умова байдужості до ризику: U (M (Х)) = M (U (Х)); в) величина сподіваного виграшу збігається з детермінованим еквівалентом лотереї ( · Твердження 3. При зростаючій функції корисності для всіх невироджених лотерей особа, яка приймає рішення, тоді і тільки тоді є: а) несхильною до ризику, коли премія за ризик є додатною (p (Х) > 0); б) схильною до ризику, коли премія за ризик є від’ємною (p (Х) < 0); в) нейтральною до ризику, якщо премія p(Х) = 0. 19. Криві байдужості та їх використання. У теорії ризику цінних паперів широке застосування [15] мають функції корисності виду
де m — величина сподіваного прибутку (ефективності тощо), s — величина ступеня ризику (середньоквадратичне відхилення або семіквадратичне відхилення тощо). Інтерпретація функції U (m, s) така: інвестор вважає за корисне для себе збільшення значення ефективності, але уникає відхилення цієї ефективності від сподіваного значення. Чим більше значення k, тим тенденція уникнення ризику, що породжується невизначеністю, проявляється більшою мірою. А тому величину k можна вважати числовою мірою тенденції інвестора щодо уникнення ризику (мірою несхильності до ризику). Значення величини k є індивідуальним для кожного інвестора, але в принципі його можна оцінити, спостерігаючи, наприклад, за тим, як інвестор ділить свій портфель цінних паперів на ризикову та безризикову частини. Якщо тепер покласти U (m,s) = m 2 – k s2 = U = const, то, відкладаючи на осі абсцис значення сподіваної ефективності, а на осі ординат — величину ступеня ризику і надаючи різні значення константі U, отримуємо сімейство кривих (рис.4.6): m 2 – k s2 = Ui, i = 1,2,.... Це сімейство кривих (в даному випадку гіпербол) в теорії функцій багатьох змінних називають лініями рівня, а в теорії корисності — кривими байдужості. На рис.4.6 побудовано криві байдужості для певної особи (коефіцієнт k — фіксований (k = const)).
Рис. 4.6. Криві байдужості особи (різні рівні функції корисності) Криві байдужості можна трактувати як різні значення рівнів функції корисності. Наприклад, крива, позначена буквою А, окреслює всі ті можливі величини норми прибутку і ризику, при яких рівень корисності даної особи становить 9 одиниць. Переміщення вздовж цієї кривої буде зберігати один і той самий рівень корисності, який становить 9 одиниць. Одна й та сама величина функції корисності може бути досягнута при великій нормі прибутку і відповідно до більшого ступеня ризику. Тобто, щоб збільшити норму прибутку і водночас залишитися при тій же самій величині корисності, треба обтяжувати себе більшим ступенем ризику. Нерідко зміни значень норми прибутку і ризику призводять до зміни рівня корисності. Наприклад, зростання норми прибутку при незмінному ступені ризику (рис. 4.6) означає перехід на іншу, «правішу», криву байдужості, що відповідає більшому значенню величини функції корисності. На рис.4.6 цій ситуації відповідає перехід з точки А до точки В. Аналогічно зменшення ступеня ризику при незмінній нормі прибутку означає перехід на криву байдужості, що відповідає більшій величині функції корисності. На рис. 4.6 цій ситуації відповідає перехід з точки А до точки С. На рис. 4.7 порівнюються криві байдужості виду U (m, s) трьох різних менеджерів (інвесторів) А, В, С у випадку, коли U (m, s) = 4 і відповідно kа = 1/4, kв = 1 та kс = 4. Зауважимо, що серед цих менеджерів особа А характеризується найбільшою схильністю до ризику, а особа С — найменшою (найбільшою несхильністю) до ризику.
Розглянемо точки А, В і С, що лежать на кривих байдужості, які відповідають величині корисності в 4 одиниці. Усім цим точкам відповідає також однакова величина ризику, яка становить 7%. Однак норми прибутку є для цих трьох осіб різними, для А — 4%, для В — 7,3%, для С — 14,1%. Це означає, що при ступені ризику s = 7 менеджер С мусить мати гарантовану (сподівану) норму доходу, яка становить 14,1% (при цьому його корисність становить 4 одиниці). З точки зору менеджера А достатньою є прибутковість, що становить 4%. Менеджер С є найменш схильним до ризику серед цих трьох осіб, бо вимагає більшої компенсації (премії, тобто норми прибутку) за обтяження таким самим ступенем ризику. Чим більш схильною до ризику є певна особа, тим більший кут нахилу до осі абсцис мають асимптоти кривих байдужості цієї особи (тим більшим є коефіцієнт варіації). 20. Суть управління портфелем цінних паперів. Диверсифікація як спосіб зниження ризику. Диверсифікація — це процес розподілу інвестованих засобів між різними об’єктами вкладення капіталу з метою зниження ступеня ризику, забезпечення більшої стійкості прибутків за будь-яких коливань дивідендів і ринкових цін на цінні папери (ЦП). Загальним правилом інвестора щодо диверсифікації є таке: необхідно прагнути розподілити вкладення між такими видами активів, які показали за минулі роки, по-перше,різну щільність зв’язку (кореляцію) із загальноринковими цінами (індексами) і, по-друге, протилежну фазу коливання норми прибутку між собою (цін) всередині портфеля. Ідею принципу диверсифікації та підхід до побудови оптимальних портфелів цінних паперів продемонструємо на прикладі побудови портфеля простих акцій. Управління портфелем цінних паперів (ПЦП) — це планування, аналіз і регулювання структури портфеля, діяльність щодо його формування та підтримки з метою досягнення поставлених цілей при збереженні необхідного рівня його ризику та мінімізації затрат, пов’язаних з ним. Основними цілями інвестування в ЦП у класичному аналізі є: · одержання прибутку; · збереження капіталу; · забезпечення приросту капіталу (на базі зростання курсової вартості цінних паперів). Досягнення цих цілей потребує дотримання певних умов. Так, наприклад, ціль «збереження капіталу» може бути реалізована тоді, коли портфель складають ліквідні ЦП. Такі цілі можуть бути до певної міри альтернативними (суперечити одна одній) та відповідати різним типам ПЦП. Наприклад, якщо метою є одержання відсотка, то пріоритет віддається «агресивним» портфелям, які складаються з низьколіквідних та високоризикованих ЦП молодих компаній, здатних, якщо цьому сприятимуть обставини, принести високі відсотки. І навпаки, якщо найважливішим для інвестора (менеджера) є збереження і приріст капіталу, то в портфель будуть залучені ЦП, що мають більшу ліквідність і які випущені відомими фірмами та державою, з невеликими ризиками й заздалегідь очікуваними сподіваними (середніми), хоча й невеликими відсотковими сплатами. 21. Норма прибутку та ризик цінних паперів. Кореляція цінних паперів та її застосування. Основною характеристикою кожного цінного паперу є норма прибутку. ЇЇ визначають як відношення прибутку, котрий приносить цінний папір, до затрат, пов’язаних з купівлею цього цінного паперу. Всі рішення щодо інвестування у цінні папери стосуються майбутнього, тому значення норми прибутку пов’язане з невизначеністю, тобто рішення щодо інвестування у цінні папери приймаються за умов ризику. Доцільно прийняти гіпотезу, що норма прибутку цінних паперів є випадковою величиною. Це означає, що норма прибутку приймати різні значення з певними ймовірностями настання цих значень. Ці ймовірності залежать від ситуації на ринку цінних паперів, тобто загалом від різних станів, в яких може перебувати економічне середовище. Отже, маючи різні можливі норми прибутку, що передбачаються в майбутньому, можна визначити середню очікувану норму прибутку цінного паперу, яку називають сподівану норму прибутку і обчислюють за формулою: Другою важливою характеристикою кожного цінного паперу є його ризик. Для кількісної оцінки міри ризику застосовують показник варіації(дисперсії) норми прибутку цінного паперу та показник середньоквадратичного відхилення норми прибутку цінного паперу. Варіацію (дисперсію) обчислюють за формулою: Середньоквадратичне відхилення розраховують за формулою: Під час формування ПЦП важливу роль відіграє ще одна характеристика ЦП – кореляція, яка характеризує взаємозв’язок між нормами прибутку двох цінних паперів. Міру цілісності (тісноти) цього зв’язку обчислюють за допомогою коефіцієнта кореляції: Коефіцієнт кореляції має наступні властивості: 1) р1,2 У випадку наявності інформації про норми прибутку акції у минулому коефіцієнт кореляції 22. Оцінка ризику цінних паперів. Важливою характеристикою кожного цінного паперу є його ризик. Для кількісної оцінки міри ризику застосовують показник варіації (дисперсії) норми прибутку цінного паперу. Варіацію обчислюють за формулою:
Де V- варіація(дисперсія), тобто міра ризику цінного паперу.
m- сподівана норма прибутку цінного паперу. Середньоквадратичне відхилення розраховуються за формулою:
σ- середньоквадратичне відхилення, міра ризику цінного паперу. У випадку, коли є статистичні дані щодо минулого, варіацію обчислюють за формулою:
Де T- кількість періодів, що минули, протягом яких спостерігались норми прибутку (роки,місяці,тижні). t- індекс номеру періоду
23. Формування портфеля цінних паперів (портфель з двох акцій). Надалі будемо вважати, що для акцій A1 та A2 мають місце співвідношення: m 1 > m 2, s 1 > s 2. Власне, це визначає доцільність утворення портфеля з цих акцій. Структура портфеля з двох видів ЦП задається вектором
Нехай
Ця парабола в системі координат «
а) б) Рис. 2.1.8. Залежність оцінки ризику ПЦП від: а) х — частки акції першого виду; б) mП — сподіваної норми прибутку ПЦП Легко переконатись [7], що Дослідження з теорії портфеля часто здійснюють у системах координат «х — s» або «т — s», при цьому дуга È А2О*А1 (область допустимих ПЦП) також опукла вниз на досліджуваному інтервалі зміни аргументу ( Координати вершини параболи
де Сутність ефекту диверсифікації полягає в тому, що збільшення сподіваної норми прибутку mП (починаючи з мінімального можливого значення) на певному етапі може супроводжуватися зменшенням оцінки ризику ПЦП — Згідно з рис. 2.1.8 б, за збільшення mП від m 2 до Оскільки 24. Формування портфеля цінних паперів (портфель з багатьох акцій). Перейдемо тепер до загального випадку, коли до складу ПЦП залучено N (N > 2) різних акцій. Розглянемо, наприклад, три акції, що мають норми прибутку відповідно 15%, 10%, 5%, середньоквадратичні відхилення 10%, 7%, 3% і коефіцієнти кореляції r23 = – 0,2; r12 = – 0,4; r13 = + 0,6. У системі координат mП – sП (норма прибутку — ризик, рис.7.5) побудуємо точки А1, А2, А3, що відповідають однорідним ПЦП, сформованим з відповідних акцій. На цьому ж рисунку побудуємо лінії (дуги), що відповідають ПЦП, сформованому з двох видів акцій (ÈА3А1; ÈА3А2; ÈА2А1).
Рис. 7.5. Множина допустимих портфелів цінних паперів Точкам К Î È А3А2 та L Î È А2А1 відповідають певні ПЦП, cформовані з двох (відповідно А3, А2 та А2, А1) видів акцій. Для цих портфелів можна розрахувати норми прибутку і ризики. Вважатимемо тепер, що кожний з цих портфелів є певного виду «цінним папером» відповідно К та L. А тому, в свою чергу, можна сформувати новий ПЦП для ЦП К та L. Такі ПЦП вже будуть включати по три акції (А1, А2, А3) і їм відповідає дуга ÈКL. Міркуючи таким чином, приходимо до висновку, що кожна точка, яка належить до заштрихованої області (рис. 7.5), відповідає деякому ПЦП, сформованому з трьох видів акцій. Допустимою множиною ПЦП називається область, точки якої характеризують ступінь ризику та норму прибутку портфеля за всіх можливих часток окремих акцій в портфелі (на рис. 7.5 — це область, обмежена жирною лінією.), Особливістю дуги ÈО*А1, яка належить допустимій множині, є те, що для будь-якої точки цієї дуги не можна вказати іншої точки допустимої області, для якої ПЦП був би кращим. Ефективною множиною ПЦП називаються ті портфелі, що відповідають точкам дуги ÈО*А1. Тобто ефективним портфелем вважається такий, для якого в допустимій множині ПЦП не можна вказати іншого портфеля: · з тим же значенням величини сподіваної норми прибутку і меншим ступенем ризику; · з тим же значенням величини ризику і більшим значенням сподіваної норми прибутку. Очевидно, що для ПЦП, складених з двох акцій, допустима множина збігається з множиною ефективних портфелів, і вони складають дугу ÈО*А1 (рис. 7.4). Задача збереження капіталу. Сутність задачі полягає у виборі такої структури ПЦП, щоб оцінка ризику портфеля була міні- Математична модель задачі:
Портфель із мінімальним ризиком у моделі Марковіца існує завжди. Знайти структуру такого ПЦП можна, побудувавши функцію Лагранжа та визначивши її точки мінімуму [7]. Задача одержання бажаного (фіксованого) прибутку (модель Марковіца). Сутність задачі полягає у виборі такої структури ПЦП, за якої його сподівана норма прибутку буде не меншою заданого рівня — mK (mK = const), а оцінка ризику при цьому буде мінімальною. Формально це однокритеріальна задача на умовний екстремум. Математична модель задачі:
Задача забезпечення приросту капіталу. Сутність задачі полягає у виборі такої структури ПЦП, щоб його оцінка ризику не перевищувала заданого рівня — sL (sL = const) і при цьому досягалася б максимальна величина сподіваної норми прибутку. Формально, як і в попередньому випадку, це однокритеріальна задача на умовний екстремум. Математична модель задачі:
25. Оптимізація структури портфеля. Задача збереження капіталу. Сутність задачі полягає у виборі такої структури ПЦП, щоб ризик цього портфеля був мінімальним. Формальна постановка цієї задачі така:
Розв’язку задачі відповідає точка О* на рис. 7.6. Метод знаходження структури ПЦП, що задовольняє умову поставленої задачі, базується на побудові та знаходженні точки мінімуму відповідної функції Лагранжа, яке, в свою чергу, зводиться до розв’язання наступної системи лінійних алгебраїчних рівнянь [4]:
Тут l — додаткова змінна (невідома величина) поява якої спричинена використанням методу Лагранжа. Слід мати на увазі, що метод Лагранжа, запропонований для розв’язання поставленої задачі, не враховує обмежень щодо невід’ємності величин xk, тобто що xk ³ 0; k = 1,..., N. А тому розв’язок системи (7.9) необхідно проаналізувати з цієї позиції. Позначимо через Х* = { x 1*; x 2*;…; xN *} розв’язок системи (7.9). Якщо всі компоненти вектора Х * є додатними (xk * > 0, k = 1,..., N) то цей вектор описує структуру оптимального ПЦП, що відповідає точці О* (рис.7.6). Якщо серед компонент Х* виявляться від’ємні, то в шуканий ПЦП не включається той ЦП, частка якого є від’ємною і найменшою серед отриманих від’ємних часток. Після вилучення цього ЦП знову розраховується структура оптимального ПЦП, складеного з (N – 1) ЦП. Процес вилучення такого роду «несприятливих» ЦП продовжується до тих пір, поки частки всіх ЦП, включених у портфель, не стануть позитивними.
Рис. 7.6. Геометрична інтерпретація задач 26. Оптимізація структури портфеля. Задача одержання бажаного (фіксованого) прибутку Сутність задачі полягає у виборі такої структури ПЦП, щоб сподівана норма прибутку цього портфеля була не меншою від зафіксованого рівня mc (mc = const) і його ризик при цьому був мінімальним. Формально цю задачу запишемо у вигляді таких співвідношень:
Розв’язку задачі одержання прибутку відповідає точка «К» на рис.7.6. Для знаходження структури ПЦП, що задовольняє умовам поставленої задачі, як і раніше, скористаємось методом Лагранжа [4], який зводиться до знаходження розв’язку системи лінійних алгебраїчних рівнянь:
де l1,l2 — додаткові змінні (невідомі величини), поява яких спричинена використанням методу Лагранжа.
27. Оптимізація структури портфеля. Включення в портфель безризикових цінних паперів. Розрахунок структури ринкового портфеля.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.013 с.) |







 Рис.4.4. Функція схильності-несхильності до ризику (С-НСР)
Рис.4.4. Функція схильності-несхильності до ризику (С-НСР)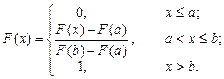

 ), а тому премія за ризик p(Х) = 0.
), а тому премія за ризик p(Х) = 0.

 Рис. 4.7. Криві байдужості трьох менеджерів (однакові рівні функцій корисності)
Рис. 4.7. Криві байдужості трьох менеджерів (однакові рівні функцій корисності)
 , де m – сподівана норма прибутку цінного паперу; рі – імовірність і-ої величини норми прибутку цінного паперу; Ri – можливе значення норми прибутку, яке може мати цінний папір, коли економічне середовище знаходиться в стані і.
, де m – сподівана норма прибутку цінного паперу; рі – імовірність і-ої величини норми прибутку цінного паперу; Ri – можливе значення норми прибутку, яке може мати цінний папір, коли економічне середовище знаходиться в стані і. де V – варіація(дисперсія), тобто міра ризику цінного паперу.
де V – варіація(дисперсія), тобто міра ризику цінного паперу. , де
, де  – середньоквадратичне відхилення, тобто міра ризику цінного паперу.
– середньоквадратичне відхилення, тобто міра ризику цінного паперу. , де p1,2 – коефіцієнт кореляції двох звичайних акцій виду 1 та виду 2; m1, m2 – сподівані норми прибутку відповідно акцій виду 1 та виду 2; Ri1, Ri2 – можливі норми прибутку, які можуть одержати відповідно акції виду 1 та виду 2, коли економічне середовище перебуває у стадії і;
, де p1,2 – коефіцієнт кореляції двох звичайних акцій виду 1 та виду 2; m1, m2 – сподівані норми прибутку відповідно акцій виду 1 та виду 2; Ri1, Ri2 – можливі норми прибутку, які можуть одержати відповідно акції виду 1 та виду 2, коли економічне середовище перебуває у стадії і;  – середньоквадратичні відхилення норм прибутку відповідно акцій виду 1 та виду 2; рі – імовірність відповідних можливих норм прибутку у і-му економічному стані.
– середньоквадратичні відхилення норм прибутку відповідно акцій виду 1 та виду 2; рі – імовірність відповідних можливих норм прибутку у і-му економічному стані. ; 2) абсолютна величина коефіцієнта кореляції р1,2 вказує на силу зв’язків між нормами прибутку акцій виду 1 та виду 2:
; 2) абсолютна величина коефіцієнта кореляції р1,2 вказує на силу зв’язків між нормами прибутку акцій виду 1 та виду 2:  – зв'язок тіснішає;
– зв'язок тіснішає;  – зв'язок слабшає. 3) знак коефіцієнта кореляції
– зв'язок слабшає. 3) знак коефіцієнта кореляції  вказує на напрямок зв’язку норм прибутку акцій:
вказує на напрямок зв’язку норм прибутку акцій:  – прямо пропорційний зв'язок між нормами прибутку акцій виду 1 та виду 2 (взаємодоповнюючі товари);
– прямо пропорційний зв'язок між нормами прибутку акцій виду 1 та виду 2 (взаємодоповнюючі товари);  – обернено пропорційний зв'язок між нормами прибутку акцій виду 1 та виду 2 (взаємозамінні товари).
– обернено пропорційний зв'язок між нормами прибутку акцій виду 1 та виду 2 (взаємозамінні товари).

 - можливе значення норми прибутку, яке може мати цінний папір, коли економічне середовище знаходиться в стані і.
- можливе значення норми прибутку, яке може мати цінний папір, коли економічне середовище знаходиться в стані і.

 - норма прибутку цінних паперів, що мала місце у період t.
- норма прибутку цінних паперів, що мала місце у період t. , а випадкова величина норми прибутку, сподівана норма прибутку й оцінка ступеня ризику визначаються відповідно за формулами:
, а випадкова величина норми прибутку, сподівана норма прибутку й оцінка ступеня ризику визначаються відповідно за формулами: ;
;  ;
;  ;
;

 ,
,  ,
,  , тоді:
, тоді: .
. » проходить через точки А1 (1;
» проходить через точки А1 (1;  ) та А2 (0;
) та А2 (0;  ), які відповідають однорідним портфелям, складеним відповідно з ЦП А 1 та А 2 (рис. 2.1.8 а).
), які відповідають однорідним портфелям, складеним відповідно з ЦП А 1 та А 2 (рис. 2.1.8 а).
 тобто задана парабола є опуклою вниз і досягає свого мінімального значення у точці (вершині)
тобто задана парабола є опуклою вниз і досягає свого мінімального значення у точці (вершині)  .
. чи
чи  ).
). :
: ,
,
 ,
,  .
. .
. оцінка ризику ПЦП зменшується від
оцінка ризику ПЦП зменшується від  до
до  . Подальше збільшення mП (від
. Подальше збільшення mП (від  до m 1) призводить до збільшення оцінки ризику від
до m 1) призводить до збільшення оцінки ризику від  до
до  Отже, диверсифікація ефективна, коли абсциса
Отже, диверсифікація ефективна, коли абсциса  , то з формули для обчислення х* отримуємо
, то з формули для обчислення х* отримуємо  , тобто r12 Î
, тобто r12 Î  . Отже, для портфеля з двох видів ЦП диверсифікація ефективна, коли коефіцієнт кореляції їх норм прибутку — r 12, належить проміжку [–1;r'), де r' =
. Отже, для портфеля з двох видів ЦП диверсифікація ефективна, коли коефіцієнт кореляції їх норм прибутку — r 12, належить проміжку [–1;r'), де r' = 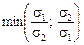 . Наголосимо, що чим менше значення r 12, тим меншим буде ризик портфеля й ефективнішою — диверсифікація.
. Наголосимо, що чим менше значення r 12, тим меншим буде ризик портфеля й ефективнішою — диверсифікація.
 ,
, 
 ;
;  ;
; 
 ;
;  ;
;  ;
;
 (7.9)
(7.9)
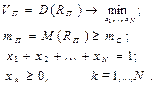
 , (7.10)
, (7.10)


