
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок структури ринкового портфеляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Запишемо рівняння (7.17) у вигляді:
Оскільки
де Іншими словами, ринковим є такий ПЦП з множини допустимих портфелів, який забезпечує мінімум відношення між зростаючим ступенем ризику та додатковим прибутком порівняно з ЦП, що мають фіксовану норму прибутку. Розв’язання поставленої задачі зводиться [2] до розв’язання системи лінійних алгебраїчних рівнянь:
де
отримуємо:
28. Оптимізація структури портфеля. Задача Тобіна. Суть задачі Д. Тобіна полягає у виборі такої структури ПЦП, щоб при мінімальному ризику грошові ресурси були розподілені між ризиковими та безризиковими ЦП і щоб сподівана норма прибутку була не меншою фіксованого рівня (mC). Формальна постановка цієї задачі має такий вигляд: VП = D (RП) ®
x 1 + x 2 +... + xN+ 1 = 1,
(тут хN+ 1 — частка вкладень з гарантованою нормою прибутку). Очевидно, що задачу Д.Тобіна можна розглядати як задачу одержання бажаного прибутку, яка розглядалась у пункті 7.8.3.2. Розв’язання цієї задачі звелось до розв’язання системи лінійних алгебраїчних рівнянь (7.10). З урахуванням того, що для безризикових ЦП виду А N+1(mN+ 1,s N+ 1) сподівана норма прибутку mN+ 1 = RF, величина ризику s N+ 1 = 0,значення коваріацій s1, N+ 1 = s2, N+ 1 =... = s N , N+ 1 = 0і при цьому l1 = – l2 RF, система (7.10) зводиться до такої системи лінійних алгебраїчних рівнянь:
Розглянемо перших N рівнянь системи (7.19). Якщо покласти Згідно з результатом попереднього пункту yE = l xE, а тому
З урахуванням отриманого, для лівої частини (N + 1) - го рівняння системи (7.19) має місце співвідношення:
а з урахуванням правої частини цього рівняння отримуємо, що
Якщо покласти mC = RF, то хN+ 1 = 1, тобто інвестор весь свій капітал розмістив у ЦП, необтяжені ризиком. Якщо ж mC = mE, то xN+ 1 = 0, тобто весь капітал інвестується у ринковий портфель. Виходячи з отриманих результатів, легко встановити, що mП = mC;s П = 29. Основні поняття гри. Поняття конфліктної ситуації та стратегії гравця. Нижня та верхня ціна гри. Конфліктною називається ситуація, в якій стикаються інтереси двох чи більше сторін, що мають суперечливі цілі, причому виграш кожної із сторін залежить від того як поводитимуться інші сторони. Приклади конфліктних ситуацій: бойові дії, біржові угоди, різні види виробництва в умовах конкуренції, угоди на фондовому ринку, спортивні змагання, інші змагання, ігри. Математична теорія конфліктних ситуацій називається теорією ігор. Теорія ігор історично виникла у зв’язку з визначенням оптимальної поведінки в азартних іграх і зберегла свою назву дотепер, хоча її застосовують і для аналізу інших конфліктних ситуацій. Метою теорії ігор є вироблення рекомендацій щодо розумної поведінки учасників конфлікту. У теорії ігор розроблена система власних понять: · Математична модель конфлікту називається грою; · Сторони у конфлікті називаються гравцями; · Результат гри називається виграшем або нічиєю; · Правилами гри називається перелік прав і обов’язків гравців; · Ходом називається вибір гравцям однієї з передбачених правилами гри дій. Ходи бувають особисті і випадкові. Особистий хід – це свідомий вибір гравця. Випадковий хід – вибір дії, що не залежить від його волі. Залежно від кількості можливих ходів у грі, ігри поділяються на: а) скінченні – ті, які передбачають скінченне число ходів; б) нескінченні – ті, які передбачають нескінченне число ходів. · Стратегією гравця називають сукупність правил, що визначають вибір варіанта дії у кожному особистому ході; · Оптимальною стратегією гравця називається така стратегія, що забезпечує йому максимальний виграш; · Завдання теорії ігор полягає у виявленні оптимальної стратегії; · Ігри, що складаються тільки з випадкових ходів, називаються азартними, ними теорія ігор не займається. Її мета – оптимізація поведінки гравця у грі, де поряд з випадковими є особисті ходи. Такі ігри називаються стратегічними; · Гра називається грою з нульовою сумою, якщо сума виграшів всіх гравців дорівнює 0, тобто кожен виграє за рахунок іншого; · Гра називається парною, якщо в неї грають два гравці. Парна гра з нульовою сумою називається антагоністичною. Теорія таких ігор найбільш розвинена. Крім того, такі ігри моделюють великий клас реальних конфліктів. В подальшому розглядатимемо саме антагоністичні ігри. Основне припущення, на підставі якого знаходять оптимальні рішення в теорії ігор, полягає в тому, що супротивник такий же розумний, як і сам гравець. Гру зручно відображати таблицею, яка називається платіжною матрицею або матрицею виграшів. Платіжна матриця має стільки стовпців, скільки стратегій у гравця В, і скільки рядків, скільки стратегій у гравця А. на перетині рядків і стовпців, що відповідають різним стратегіям, стоять виграші гравця А і, відповідно, програші гравця В:
Якщо задача зведена до матричної форми, то можна порушувати питання про пошук оптимальних стратегій. Для цього введемо поняття верхньої і нижньої ціни гри. Нижньою ціною гри називається елемент матриці, для якого виконується умова: Нижня ціна гри Верхньою ціною гри називається елемент матриці, що задовольняє умову: Верхня ціна гри Точка(елемент) матриці, для якої виконується умова 30. Методи знаходження оптимальних стратегій гравців. При аналізі платіжної матриці можливі 2 випадки: Випадок 1. Платіжна матриця має сідлову точку. Оскільки прийнято умову максимальної розумності гравців, то саме ті рядок і стовпець, які відповідають сідло вій точці, і є оптимальними стратегіями. Стратегії, які відповідають сідло вій точці, є найбільш вигідними для обох гравців, і вони називаються чистими стратегіями. Метод вибору стратегії на основі сідловок точки називаються «принцип мінімаксу», який інтерпретується так: чини так, щоб при найгіршій для тебе поведінці супротивника одержати максимальний виграш. Випадок 2. Платіжна матриця не має сідловок точки. Це найбільш поширений випадок. У цій ситуації теорія пропонує використовувати змішані стратегії, тобто стратегії, у яких випадковим чином чергуються особисті стратегії. Точний метод пошуку оптимальної змішаної стратегії зводиться до задачі лінійного програмування, хоч і не є складний, але трудомісткий. Розглянемо принцип знаходження змішаних стратегій. Якщо в матричній грі відсутня сідловка точка в чистих стратегіях, то знаходять Змішана стратегія гравця – це повний набір застосування його чистих стратегій при багаторазовому повторенні гри в тих самих умовах із заданними ймовірностями. Умови застосування змішаних стратегій є наступними: - Гра без сідловок точки; - Гравці використовують випадкове поєднання чистих стратегій із завданнями ймовірностями; - Гра багаторазово повторюється у подібних умовах; - При кожному з ходів жоден гравець не інформований про вибір стратегії іншим гравцем4 - Допускаються усереднення результатів ігор. - Для гравця А змішана стратегія, що полягає у застосуванні чистих стратегій А1, А2,…, Аm з відповідними ймовірностями р1, р2,…, рm позначається матрицею - S1 = - Для гравця В відповідно: S1 = - При заданих векторах - Отже, розв’язком матричної гри є: 1) - Змішані стратегії будуть оптимальними, якщо вони утворюють сідлову точку для функції М(А, - - Слід зазначити, що при виборі оптимальної стратегії, гравцю А завжди буде гарантований середній виграш, не менший, ніж 31. Сутність теоретико-ігрової моделі. Під теорією гри розуміють теорію математичних моделей та методів, пов’язаних з прийняттям раціональних рішень в умовах конфлікту та невизначеності. Широко відомою моделлю прийняття рішень в умовах невизначеності є статична модель, породжена теоретико-ігровою концепцією. Згідно з концепцією теорії гри ситуація прийняття рішень характеризується множиною { X;Q; F }, де Х — множина рішень (стратегій) суб’єкта керування (1-го гравця), Q — множина станів (стратегій) економічного середовища (ЕС) (2-го гравця), F = { f (x,q); х Î Х;qÎQ} — функціонал оцінювання (ФО), визначений на множині Х ´Q і такий, що набуває значення з простору Для дослідження статистичних моделей за умов невизначеності, конфліктності й зумовленого ними ризику використовують схему гри з економічним середовищем. Під економічним середовищем зазвичай розуміють сукупність невизначених чинників (зокрема, й економічних), які впливають на ефективність рішення. Складовими такої гри є: 1) перший гравець ― суб’єкт прийняття рішення (СПР), вибір стратегії поведінки якого базується на множинні 2) другий гравець — економічне середовище, яке може перебувати в одному з n взаємовиключних станів 3) відсутність у СПР апріорної інформації про те, в якому зі своїх станів перебуватиме економічне середовище (які рішення прийме другий гравець); 4) точне знання СПР функціонала оцінювання 32. Статичні ігри в умовах ризику та невизначеності. Статистичні ігри – це гра двох осіб людини і природи з використанням людиною додаткової статистичної інформації про стан природи. Тут природа не є розумним гравцем, що прагне вибрати для себе оптимальні стратегії. Цей гравець не зацікавлений у виграші. Людина у даному випадку статистик, вона має справу з уявлюваним супротивником, тобто з природою. Гравець-природа не обира оптимальної стратегії, а статистик повинен прагнути до визначення розподілу імовірностей стану природи. Статистик(гравець А) – намагається діяти обачно, використовуючи мінімаксну стратегію, що дозволяє одержати найменший програш. Гравець-природа діє зовсім випадково, можливість стратегії визначається як її стан, наприклад умоаи погоди, попит на продукцію, обсяг перевезень і т.п. У статистичних іграх використовуютья такі поняття: функція ризику, функція витрат, функція рішень. Умови шри задаються у вигляді матриці А=|аіj| це множина рішень статистика. B=|bij| це множина рішень природи. Елемент аіj дорівнює виграшу гравця А, якщо він використовує стратегію аіj, а природа має стан bj. У ряді випадків при розв’язанні гри використовують матрицю ризиків R=|rij|. Елементи матрицы ризику rij це різниця між виграшем, що одержав би статистик А, якби знав стан природи bj, і виграшем, який він одержить в тих же умовах, застосувавши стратегію ai. rij=Bj - aij Bj=maxiaij Наприклад розлянемо матрицю прибутків | 3 4 5 | А= | 6 7 8 | | 9 1 2 | __________________________ max | 9 7 8 | Побудуємо матрицю ризиків | 6 3 3 | R= | 3 0 0 | | 0 6 6 | Тому що, наприклад r11 = 9 – 3 =6: r12 = 7 – 4 = 3 і т.д. Розглянемо ряд критеріїв, використовуваних при розв’язанні ігор з природою. При відомому розподілі імовірностей станів природи критерієм прийняття рішення є максимізація виграшу чи мінімізація очікування ризику. Нехай імовірності стану природи дорівнюють ( Вибір і-ої стратегії забезпечує математичне сподівання виграшу, що дорівнює У ряды випадкыв, коли імовірності стану природи невідомі, для їхньої оцінки використвують принцип недостатнього обгрунтування Лапласа. Відповідно до нього усі стани природи вважаються рівноймовірними,тоді вибір рішення можна робити по мінімуму середньозваженого показника ризику. Якщо R – критерій ризику; H – величина втрат; Рі – імовірність настання ризикових ситуацій; R i = n – кількість розглянутих варіантів станів природи. Однак у цих випадках не можна стверджувати що приняте рішення є оптимальним. Оптимальним воно є тільки щодо прийняття розподілу імовірностей станів природию Якщо ж питання розподілу імовірностей і природи невідоме, можна скористатися: 1.Максимінним критерієм Вальда чи критерієм крайнього песимізму 2.Мінімаксним критерієм Севіджа 3.Критерієм крайнього оптимізму 4.Критерієм узагальненого максиміна Гурвіца (критерій песимізму-оптимізму)
33. Економічне середовище у ролі гравця. Поняття інформаційної ситуації та її характеристика. Економічне середовище Під економічним середовищем надалі будемо розуміти сукупність невизначених чинників (у тому числі й економічних), які впливають на ефективність рішення, що приймається. У дискретному випадку ЕС являє собою повну групу взаємовиключаючих та взаємодоповнюючих випадкових подій: Q = {q1; q2; …; qn}; Q = q1 + q2 +…+ q n; Р(Q) = Р(q1 + q2 +…+ q n) = Р(q1) + Р(q2) +... +Р(qn)=р1+р2+…+рn=1. Інформаційна ситуація Під інформаційною ситуацією з погляду суб’єкта управління (залежно від рівня його поінформованості) розуміють певний ступінь градації невизначеності щодо перебування економічним середовищем в одному зі своїх можливих станів у момент при- Класифікацію інформаційних ситуацій, які характеризують поведінку економічного середовища під час «вибору» свого стану в процесі прийняття рішення, можна побудувати таким чином [6; 7; 9]. Перша інформаційна ситуація характеризується заданим розподілом апріорних імовірностей станів економічного середовища Друга інформаційна ситуація характеризується можливістю оцінити параметри (числові характеристики), які характеризують розподіл апріорних імовірностей станів економічного се- Третя інформаційна ситуація характеризується певною системою (лінійних чи нелінійних) співвідношень пріоритету стосовно елементів множини Q — станів економічного середовища (обсяг інформації про економічне середовище недостатній). Четверта інформаційна ситуація характеризується, з одного боку, невідомим розподілом апріорних імовірностей станів економічного середовища, а з іншого — відсутністю активної протидії економічного середовища цілям суб’єкта управління. П’ята інформаційна ситуація характеризується абсолютно протилежними (антагоністичними) інтересами СПР та економічного середовища, тобто має місце конфлікт між ними. При цьому економічне середовище є активним) і являє собою зловмисного противника. (Це ситуація, коли є достатнім обсяг інформації про поведінку економічного середовища). Шоста інформаційна ситуація характеризується як проміжна між першоюта п’ятою інформаційними ситуаціями, коли разом із наявністю певної інформації щодо розподілу Р апріорних імовірностей Слід зауважити, що кожній інформаційній ситуації відповідає свій набір критеріїв прийняття рішень. 34. Функція ризику. Модель прийняття рішень в умовах ризику. Функція ризику визначається як лінійне перетворення позитивно чи негативно заданого інгредієнта ФО до відносних одиниць вимірювання. Таке перетворення встановлює порядок відліку ФО для кожного стану ЕС 1) для
і функція ризику визначається у вигляді:
2) для F=F — при фіксованому
i функція ризику визначається як
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 519; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.13.192 (0.015 с.) |

 .
. — модифікований коефіцієнт варіації ринкового портфеля Е (mE;s E), який має негативний інгредієнт (
— модифікований коефіцієнт варіації ринкового портфеля Е (mE;s E), який має негативний інгредієнт ( ), то задача розрахунку його структури зводиться до знаходження такого портфеля з множини допустимих портфелів, який задовольняв би умову:
), то задача розрахунку його структури зводиться до знаходження такого портфеля з множини допустимих портфелів, який задовольняв би умову: ,
, .
. , (7.18)
, (7.18) . Враховуючи, що
. Враховуючи, що ,
, .
. ,
,
 .
. (7.19)
(7.19) , то прийдемо до системи рівнянь (7.18) щодо знаходження структури ринкового портфеля Е (mE; s E). Позначимо розв’язок системи (7.18) через yE = (y 1, y 2, ..., yN), суму компонент розв’язку yE — через l (тобто
, то прийдемо до системи рівнянь (7.18) щодо знаходження структури ринкового портфеля Е (mE; s E). Позначимо розв’язок системи (7.18) через yE = (y 1, y 2, ..., yN), суму компонент розв’язку yE — через l (тобто 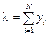 ), структуру ринкового ПЦП — через
), структуру ринкового ПЦП — через  ,
,  , а перші N компонент розв’язку системи (7.19) — через xП =
, а перші N компонент розв’язку системи (7.19) — через xП =  .
.

 Тоді
Тоді 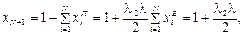 тобто
тобто 
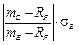 ; хП =
; хП =  -
-
 показує, що хоч би яку стратегію застосував гравець В, то гравець А гарантує собі виграш, не менший
показує, що хоч би яку стратегію застосував гравець В, то гравець А гарантує собі виграш, не менший  .
. гарантує для гравця В, що гравець А не одержить виграш, більш за величину
гарантує для гравця В, що гравець А не одержить виграш, більш за величину 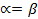 , називається сідловою точкою. У сідло вій точці найбільший з мінімальних виграшів гравця А точно дорівнює найменшому з максимальних програшів гравця В, тобто мінімум у будь-якому рядку матриці дорівнює максимальному у будь-якому стовпці.
, називається сідловою точкою. У сідло вій точці найбільший з мінімальних виграшів гравця А точно дорівнює найменшому з максимальних програшів гравця В, тобто мінімум у будь-якому рядку матриці дорівнює максимальному у будь-якому стовпці. (при чому
(при чому  ). У такій ситуації можна одержувати виграші, які в середньому більші від
). У такій ситуації можна одержувати виграші, які в середньому більші від  , при умові, що
, при умові, що  де рі – ймовірність застосування і-ої стратегії гравцем А.
де рі – ймовірність застосування і-ої стратегії гравцем А. , приумові, що
, приумові, що 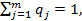 де qi –ймовірність застосування j-ої стратегії гравцем В.
де qi –ймовірність застосування j-ої стратегії гравцем В. та
та  та знаючи платіжну матрицю, можна визначити середній виграш гравця А:
та знаючи платіжну матрицю, можна визначити середній виграш гравця А: 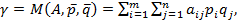 де
де  – ціна гри, тобто середній виграш гравця А при використанні обома гравцями змішаних стратегій.
– ціна гри, тобто середній виграш гравця А при використанні обома гравцями змішаних стратегій. – оптимальна змішана стратегія гравця А; 2)
– оптимальна змішана стратегія гравця А; 2)  – оптимальна змішана стратегія гравця В; 3)
– оптимальна змішана стратегія гравця В; 3)  ).
). А,
А,  (максимін це
(максимін це 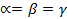 .
.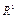 (одновимірного простору), функція f (x,q) — функція виграшу 1-го гравця (суб’єкта керування).
(одновимірного простору), функція f (x,q) — функція виграшу 1-го гравця (суб’єкта керування). взаємовиключних рішень (стратегій), одне з яких йому необхідно обрати;
взаємовиключних рішень (стратегій), одне з яких йому необхідно обрати; що утворюють множину сценаріїв
що утворюють множину сценаріїв  , один із яких обов’язково настане;
, один із яких обов’язково настане; , елемент
, елемент  якого є кількісною оцінкою ефективності результату в разі вибору ним стратегії
якого є кількісною оцінкою ефективності результату в разі вибору ним стратегії  при реалізації стану економічного середовища
при реалізації стану економічного середовища 
 Функціонал оцінювання F називають також матрицею гри, або платіжною матрицею.
Функціонал оцінювання F називають також матрицею гри, або платіжною матрицею. )
)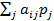


 , тобто вважаються відомими ймовірності реалізації j- го стану:
, тобто вважаються відомими ймовірності реалізації j- го стану:  , для яких мають виконуватися такі умови:
, для яких мають виконуватися такі умови: 
 ,
,  (достатня за обсягом інформація).
(достатня за обсягом інформація). ,
,  :
: , коли мають зафіксований стан економічного середовища
, коли мають зафіксований стан економічного середовища  , знаходять величину
, знаходять величину
 ;
; знаходять
знаходять
 .
.


