
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Портфель из двух видов ценных бумагСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Эффективность и риск портфеля из двух видов ценных бумаг можно оценить по формулам:
где х 1 и х 2 – ценовая доля первого и второго вида ценных бумаг, Коэффициент вариации портфеля состоящего из двух видов ценных бумаг можно определить по формуле:
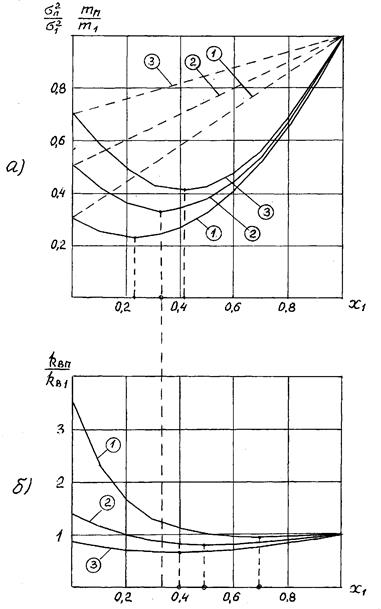
На рис. 4.1а приведены зависимости эффективности портфеля ценных бумаг 1. Эта зависимость имеет линейный характер. Эффективность портфеля ценных бумаг изменяется от 1. Из приведенных графиков видно, что риск портфеля ценных бумаг двух видов На рис. 4.1б приведены зависимости коэффициента вариации портфеля ценных бумаг 1.
Рис. 4.1. Зависимость риска независимых бумаг двух видов от ценовой доли бумаг первого вида
Из приведенных графиков видно, что при определенных оптимальных значениях х 1 имеют место минимальные значения коэффициента вариации портфеля ценных бумаг. При Оптимальные значения распределения ценовых долей бумаг х 1 и х 2 обеспечивающие минимальное значение риска портфеля При
Рис. 4.2. Зависимость риска зависимых ценных бумаг двух видов от ценовой доли бумаг первого вида Оптимальное распределение ценовых долей бумаг х 1 и х 2 обеспечивающих минимум среднеквадратического значения рисков
Графики зависимости отношения Сплошными линиями на рисунках 4.2а и б приведены зависимости отношения Оптимальное распределение ценовой доли бумаг первого и второго вида, обеспечивающие минимум коэффициента вариации портфеля ценных бумаг
4.4. Портфель из m -независимых ценных бумаг
Для независимых ценных бумаг парные коэффициенты корреляции доходностей этих ценных бумаг равны нулю:
В этом случае риск портфеля этих ценных бумаг определяется формулой:
где Определим структуру портфеля ценных бумаг минимального риска
Данная задача нахождения оптимального распределения
Для нахождения оптимальных значений
Для получения конкретных результатов далее ограничимся портфелем, состоящим из четырех видов бумаг m = 4. В этом случае система уравнений (4.16) будет включать пять уравнений, четвертое из которых будет иметь вид:
Последовательно вычитая из первого уравнения второе, затем третье и затем четвертое получим:
Определим из этих уравнений значения х 2; х 3 и х 4
Подставим эти значения в пятое уравнение системы (4.16) получим:
Отсюда для х 1 получим:
С учетом формул (4.17) для ценовых долей бумаг второго, третьего и четвертого видов получим:
Минимальное значение риска портфеля из четырех видов ценных бумаг определится формулой:
а средняя доходность такого портфеля будет равна:
Пример 4.1. Для портфеля из четырех видов ценных бумаг со средней доходностью
Найти оптимальную структуру портфеля минимального риска, его риск Решение: По формулам (4.18) находим оптимальные значения ценовых долей бумаг каждого вида.
По формуле (4.19) определяем минимальное значение риска портфеля ценных бумаг:
Для средней доходности такого портфеля получим:
Из приведенных расчетов видно риск портфеля оказался меньше, чем риск наименее рисковых бумаг первого вида
|
||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 411; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.104.132 (0.011 с.) |

 (4.11)
(4.11) - коэффициент корреляции доходностей по ценным бумагам первого и второго вида;
- коэффициент корреляции доходностей по ценным бумагам первого и второго вида; .
. (4.12)
(4.12) и рисков портфеля ценных бумаг
и рисков портфеля ценных бумаг  от ценовой доли бумаг первого вида х 1 при
от ценовой доли бумаг первого вида х 1 при  Зависимость
Зависимость  2.
2. 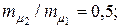 3.
3. 
 при х 1=1. Зависимость отношения
при х 1=1. Зависимость отношения  2.
2.  3.
3. 
 при определенном оптимальном значении ценовой доли бумаг х 1 может иметь минимальное значение. Так, например, при
при определенном оптимальном значении ценовой доли бумаг х 1 может иметь минимальное значение. Так, например, при  минимальное значение
минимальное значение  То есть при оптимальном распределении ценовой доли бумаг риск портфеля ценных бумаг двух видов будет меньше чем риски ценных бумаг первого и второго видов (см. п. 3.3.1).
То есть при оптимальном распределении ценовой доли бумаг риск портфеля ценных бумаг двух видов будет меньше чем риски ценных бумаг первого и второго видов (см. п. 3.3.1). от ценовой доли бумаг первого вида х 1 при
от ценовой доли бумаг первого вида х 1 при  и при трех значениях отношения:
и при трех значениях отношения: 2.
2. 
 когда эффективности ценных бумаг первого и второго вида одинаковы, минимальное значение коэффициента вариации портфеля
когда эффективности ценных бумаг первого и второго вида одинаковы, минимальное значение коэффициента вариации портфеля  ценных бумаг будет при ценовых долях бумаг первого х 1 и второго х 2 вида определяющихся формулами (3.21), а минимальное значение
ценных бумаг будет при ценовых долях бумаг первого х 1 и второго х 2 вида определяющихся формулами (3.21), а минимальное значение  определиться формулой (3.22).
определиться формулой (3.22). (рис. 4.1а), так же могут быть определены по формулам (3.21).
(рис. 4.1а), так же могут быть определены по формулам (3.21). оптимальные значения распределения ценовых долей бумаг первого х 1 и х 2 могут быть найдены дифференцированием формул (4.11) и (4.12) по х 1 и приравниваем производной нулю.
оптимальные значения распределения ценовых долей бумаг первого х 1 и х 2 могут быть найдены дифференцированием формул (4.11) и (4.12) по х 1 и приравниваем производной нулю.
 портфеля ценных бумаг можно определить по формулам:
портфеля ценных бумаг можно определить по формулам: (4.13)
(4.13) от ценовой доли бумаг первого вида х 1 при
от ценовой доли бумаг первого вида х 1 при  приведены пунктирными линиями для
приведены пунктирными линиями для  на рисунке 4.2а и для
на рисунке 4.2а и для  на рис. 4.2б. Из рисунков видно, что при отрицательных значениях коэффициента корреляции ценных бумаг имеет место оптимальное распределение ценовых долей бумаг х 1 и х 2 (4.13). При положительных значениях коэффициента корреляции ценных бумаг
на рис. 4.2б. Из рисунков видно, что при отрицательных значениях коэффициента корреляции ценных бумаг имеет место оптимальное распределение ценовых долей бумаг х 1 и х 2 (4.13). При положительных значениях коэффициента корреляции ценных бумаг 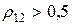 минимума значения
минимума значения  не наблюдается.
не наблюдается. и при
и при  (кривая 1) и
(кривая 1) и  (кривая 2). Из приведенных графиков видно, что оптимальные значения х 1 и х 2 обеспечивающие минимумы
(кривая 2). Из приведенных графиков видно, что оптимальные значения х 1 и х 2 обеспечивающие минимумы  и
и  (4.14)
(4.14) при
при 

 - риски доходностей ценных бумаг i -того вида, определяющиеся среднеквадратическим значением доходностей; хi – ценовая доля бумаг i -того вида.
- риски доходностей ценных бумаг i -того вида, определяющиеся среднеквадратическим значением доходностей; хi – ценовая доля бумаг i -того вида. поэтому оптимальное распределение ценовых долей ценных бумаг будем искать из условия:
поэтому оптимальное распределение ценовых долей ценных бумаг будем искать из условия: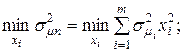 при
при  (4.15)
(4.15) может быть решена с помощью функции Лагранжа. Для задачи, формализуемой условиями (4.15) функция Лагранжа имеет вид:
может быть решена с помощью функции Лагранжа. Для задачи, формализуемой условиями (4.15) функция Лагранжа имеет вид:
 обеспечивающих минимум
обеспечивающих минимум 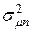 составим систему уравнений из производных функции Лагранжа по
составим систему уравнений из производных функции Лагранжа по  и λ.
и λ. (4.16)
(4.16)

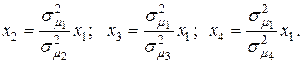 (4.17)
(4.17)
 (4.18)
(4.18)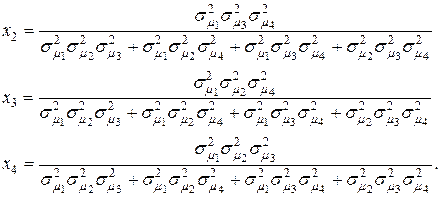 (4.18)
(4.18) (4.19)
(4.19)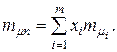
 и рисками
и рисками 
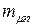 .
.





 а средняя доходность (эффективность) портфеля ценных бумаг оказывается больше, чем доходность бумаг первого вида
а средняя доходность (эффективность) портфеля ценных бумаг оказывается больше, чем доходность бумаг первого вида  Таким образом, для оптимального портфеля минимального риска коэффициент вариации портфеля ценных бумаг равен
Таким образом, для оптимального портфеля минимального риска коэффициент вариации портфеля ценных бумаг равен  и это значение меньше, чем коэффициент вариации наименее рискованных бумаг первого вида
и это значение меньше, чем коэффициент вариации наименее рискованных бумаг первого вида 



